利用常微分方程分析数码相机市场价格发展趋势

邱雯昕

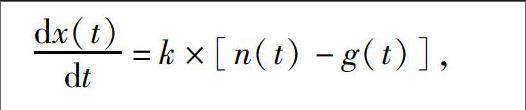
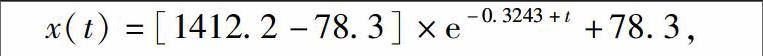
【摘要】本文采用常微分方程法，建立了模拟索尼A7系列数码相机市场价格发展趋势的数学模型.在实际建模过程中，采用收集并分析索尼A7系列相机市场价格数据—分析影响索尼A7系列数码相机市场价格变化的主要因素—建立常微分方程模型—求解—分析结果的建模思路.最终，本次研究得出结论，索尼A7系列数码相机市场价格发展规律与影响其价格变化的因素——供需量之间的相互作用在误差允许范围内符合规律，并对模型的缺陷和待改进点加以说明.

【关键词】发展趋势；常微分方程；相机市场

一、引 言

如今，数码相机已经取代传统相机的地位进入普通家庭用户，经过几代产品的发展，它的制造技术逐渐成熟，价格更趋于合理，市场竞争更加激烈.在数码相机行业有佳能、索尼、奥林巴斯、尼康等领头羊的公司，这几个公司引导着数码相机产业的未来，同时，国产品牌的数码相机公司也在积极追赶，互相之间激烈的市场争夺也在愈演愈烈.

纵观整个行业现状，不难看出，相机市场的整体结构，产品的价格定位，以及产品的普及度和关注度，都已经发生了巨大的变化，而产生这一变化，与人们对于新生事物的追求有关，与厂商大力推广和促销有关，更与人们生活水平的提高有关.

面临竞争激烈的市场情况，如何能正确认识数码相机发展趋势，有针对性的提高市场营销能力，增加市场占有率，对于业界的所有公司都十分重要.而基于一定量市场数据，对数码相机市场中的某件龙头产品的行情进行预测分析，往往能够对其余的产品进行一定指导作用.在众多对数码相机市场进行分析的方法中，利用数学建模的方法建立数学模型[1]，将市场情况表征为函数关系式以简明表示，有较为精准预测市场价格发展的作用，在分析数码相机市场价格中占有重要地位.

本文基于如上考虑，以索尼公司A7系列数码相机为主要研究对象，建立市场价格分析数学模型.

二、问题分析

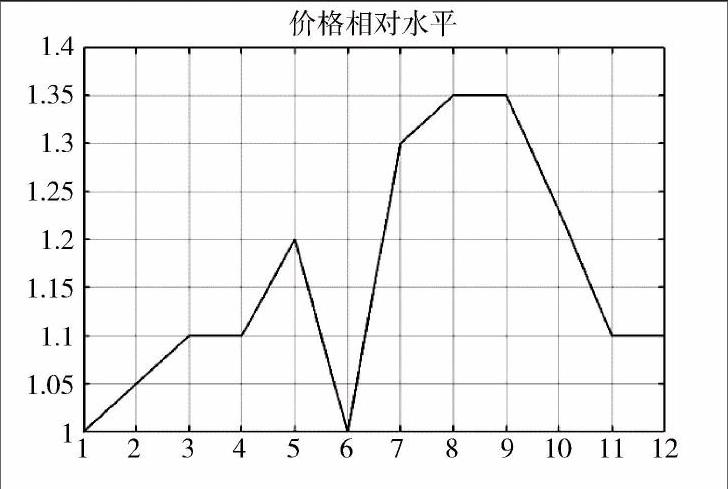
在数学模型建立之前，需要确定加以深入考虑的变量，首先选取索尼A7系列相机在市场中的平均价格数据作为模型建立前的基准.将1月份的数据作为标准值，将其余月份的平均数据加以标准化，绘制折线图.

对以上曲线结果进行简单分析，可知：该品牌相机的市场价格和月份具有一定的相关性，结合常识可得，在旅游旺季，数码相机的价格会相对较高，故选取月份作为主要考虑变量之一.

通过查阅相关资料，可以知道，影响索尼A7系列数码相机市场价格的因素不仅有市场需求量，还有索尼公司的供应量，以及市场中的相关供应链上的供需平衡情況.

此外，由于在收集信息的方面和建模能力方面存在较多的限制条件，所以本次研究忽略了可能对索尼A7系列数码相机的市场价格造成微弱影响的市场因素，仅考虑在供应链和市场需求量方面的变化对索尼A7系列数码相机的市场价格造成的影响.利用此种类似于简化法的方式对相关变量进行筛选，可以有效降低模型的复杂度.

三、方法选择

为了更好地模拟索尼A7系列数码相机的市场价格发展环境，在建立市场价格发展的数学模型时，需要考虑的要素通常有很多，相应的建立起来的数学模型就具有一定的复杂性，而通过这种方式建立的市场价格发展数学模型虽然能够较为准确地模拟和预测索尼A7系列数码相机的市场价格发展情况，但是在更广泛的区域内不具有适用性，而且在建模过程中的计算量超出了建模的价值意义.在本领域最为常见的方法是基于直接数据进行拟合，但是考虑到本案例的数据获取具有相当的局限性，且数据内生性无法规避，故弃用本方法[2].

综合考虑各种因素后，本次研究选用的依据的理论和方法是常微分方程法.

常微分方程法，顾名思义是利用常微分方程对一个复杂系统中的一系列变量进行统合.一般包含如下几个步骤：

第一步：提出实际问题，加以分析，确定式子中的因变量，自变量，不变量等.

第二步：根据实际问题的相关规律建立数学模型，即列出相关的常微分方程式.

第三步：尝试解出该常微分方程，由于常微分方程的形式总是相对固定，所以其通解的形式和方法也相对固定，解决起来往往并不复杂.

第四步：解出方程的最终结果，分析之，来解释或者对实际问题的发展进行预测，即通过数学语言总结实际情况，是重中之重[3].

四、模型建立

首先，假设在某一时刻t，所考虑的物品的单价为x（t）.而物品单价这一变量与这一时刻t中此种物品的市场需求量n（t）和供应量g（t）有关，并且，供需差和此种物品的单价之间具有相关性，相互影响，相互调节.抛开其他影响因素先不加以考虑，在这一时刻，列出此种物品的价格x（t），市场需求量和供应量之间的关系，如下式：

dx（t）dt=k×[n（t）-g（t）]，

其中，k为比例系数，在这里是一个常数.同时，可以知道，当t的取值趋向于无穷大的时候，满足式子x（t）=x′，此处的x′也为一个常数，我们将它定为稳定价格，即相机的价格不变量.

通过对上述式子的简要分析，可得出第一阶的结论，即在t时刻这种物品的单价的变化率与供需差之间成正比关系.也就是说，在不考虑影响市场价格变化的其他因素时，就供需差而言，市场价格发展可以建立的数学模型就是最基本的常微分方程[4].

五、模型数据检验

为了验证模型的准确性，选取2015年全年度数据作为主要数据集加以考查，其中供给量数据由厂商财务报告查询得到，需求量数据由公司预测数据得到，销量由年报得到，并将数据带入最后式子，可得

x（t）=[1412.2-78.3]×e-0.3243+t+78.3，

再将结果与实际值进行比较，得出平均误差率为219%，即准确率为68.1%，这一结果对于本模型来说，是相当不错的结果.

六、模型缺陷和改进点

纵观整个模型，主要缺陷在于模型的复杂度不能满足实际需求，在一个衡量市场的复杂系统中，仅仅通过时间，需求量和供给量几个简单变量加以确定销量的函数，并不能称得上是完全准确的.在对本模型的进一步深入研究中，必须要考虑竞争者的存在来完善模型.在该研究层面上，将考虑多种外界因素的协同作用和反馈作用.同时，数据量的不足也会造成结果的准确性评估不具有一定的参考意义，这也是值得考虑的问题.

七、结 论

综合以上的推导过程和函数结果，并进一步结合实际情况分析，我们可以得出结论，在以索尼A7系列为代表的一般数码相机市场中，当时间推演趋近于无穷大时，其平均单价将会始终趋近于一个稳定值x′，这代表了通过整个市场的调节，一件商品的价值始终会围绕一个固定值上下摆动，该固定值即为物品使用价值的一个表征.

利用数学语言加以说明，即如果在开始研究的时刻，即0时刻，初值即到了该稳定值，那么在研究过程中这种物品的单价将稳定在这个常数左右，没有外力干扰时，不再变化.

在建立索尼A7系列数码相机市场价格发展数学模型的过程中，运用常微分方程建立模型具有思路简单，条理清晰的特点，但同时应用常微分方程法建模时，忽略了供应量和需求量之间的互相调配关系，也存在一定的不足.在仅考虑市场的需求量和供应量对某种物品的单价的影响的时候，通过常微分方程理论体系建立的某种物品的市场价格发展数学模型在误差允许范围内可以说是准确的，即可以用此模型预测某种物品的市场价格发展趋势.

建立市场价格发展数学模型，不仅可以通过常微分方程进行模拟，也可以通过其他方式建立数学模型，但是经过对很多文献的总结分析，可以发现，通过常微分方程的方法建立数学模型的过程最为方便准确.

【参考文献】

[1]方芳.常微分方程理论在数学建模中的简单应用[D].合肥：安徽大学，2010.

[2]张秋生.单步法求解常微分方程初值问题[J].科技通报，2012（2）：7-9.

[3]李宝萍.常微分方程在数学建模中的应用[J].赤峰学院学报（自然科学版），2012（21）：1-2.

[4]任瑞芳.常微分方程理论的形成[D].西安：西北大学，2008.