航空发动机高压转子-滚动轴承系统非线性动力响应分析*
2018-03-14崔颖黄宇熙王永亮孙鹏
崔颖 黄宇熙 王永亮 孙鹏
(大连海事大学 船舶与海洋工程学院, 大连 116026)
引言
转子-滚动轴承系统是航空发动机的核心部件,其振动特性对整机的安全可靠运行具有重要影响.转子-滚动轴承系统在运转过程中会出现分岔、混沌等非线性动力学现象[1-3],危害转子工作的稳定性.转子-滚动轴承系统非线性动力学分析的首要是动力学建模,目前针对转子系统的研究中,大多建立了较为简单的低维单盘转子模型[4-9],或是考虑联轴器、阻尼器、机匣等部件的高维复杂模型[10].
滚动轴承非线性力是使转子-滚动轴承系统产生非线性振动现象的主要根源.研究发现:转子-滚动轴承系统会产生频率与滚珠通过载荷作用线频率相同的振动,这种振动被称为VC振动[11-14].显然,VC振动与滚动轴承结构参数密切相关,Sunnersjö[15]开展了关于VC振动的数值与实验研究,并指出VC振动的发生不受轴承精度影响,Futaka[16]等采用典型的2自由度滚动轴承模型进行了计算,结果显示系统在临界转速附近存在VC亚谐振动,Mevel[17]等试验给出了滚动轴承转子系统VC振动的波形,并分析了系统通过亚谐振动与准周期运动进入混沌的路径.然而,VC振动随转子-滚动轴承系统参数变化的规律还有待深入的研究.
本文采用Timoshenko梁单元模型结合滚动轴承的非线性支撑力模型,建立了航空发动机高压转子-滚动轴承系统的24自由度高维动力学模型,利用自适应步长Newmark-β法[18,19]对该系统模型进行了计算,分析了系统非线性动力响应随转速的变化规律,并着重计算分析了不平衡量、轴承游隙对低转速区VC振动的影响.
1 高压转子-滚动轴承系统动力学模型
现代典型的航空发动机高压转子-滚动轴承系统结构的简化模型如图1.采用有限元法将该模型分为5个单元6个结点,结点1处作用滚动轴承1#,结点6处作用中介轴承2#,模型具体参数如表1所示.
基于Timoshenko梁单元,建立考虑系统的运动微分方程组:
(1)
式中,M为质量矩阵;C为阻尼矩阵;J为陀螺矩阵;K为刚度矩阵;Ω为转子转速;广义位移向量U={x1,y1,-θx1,θy1,…,x6,y6,-θx6,θy6}T;Fg为重力;Fb为滚动轴承非线性支撑力;Fe为不平衡力.
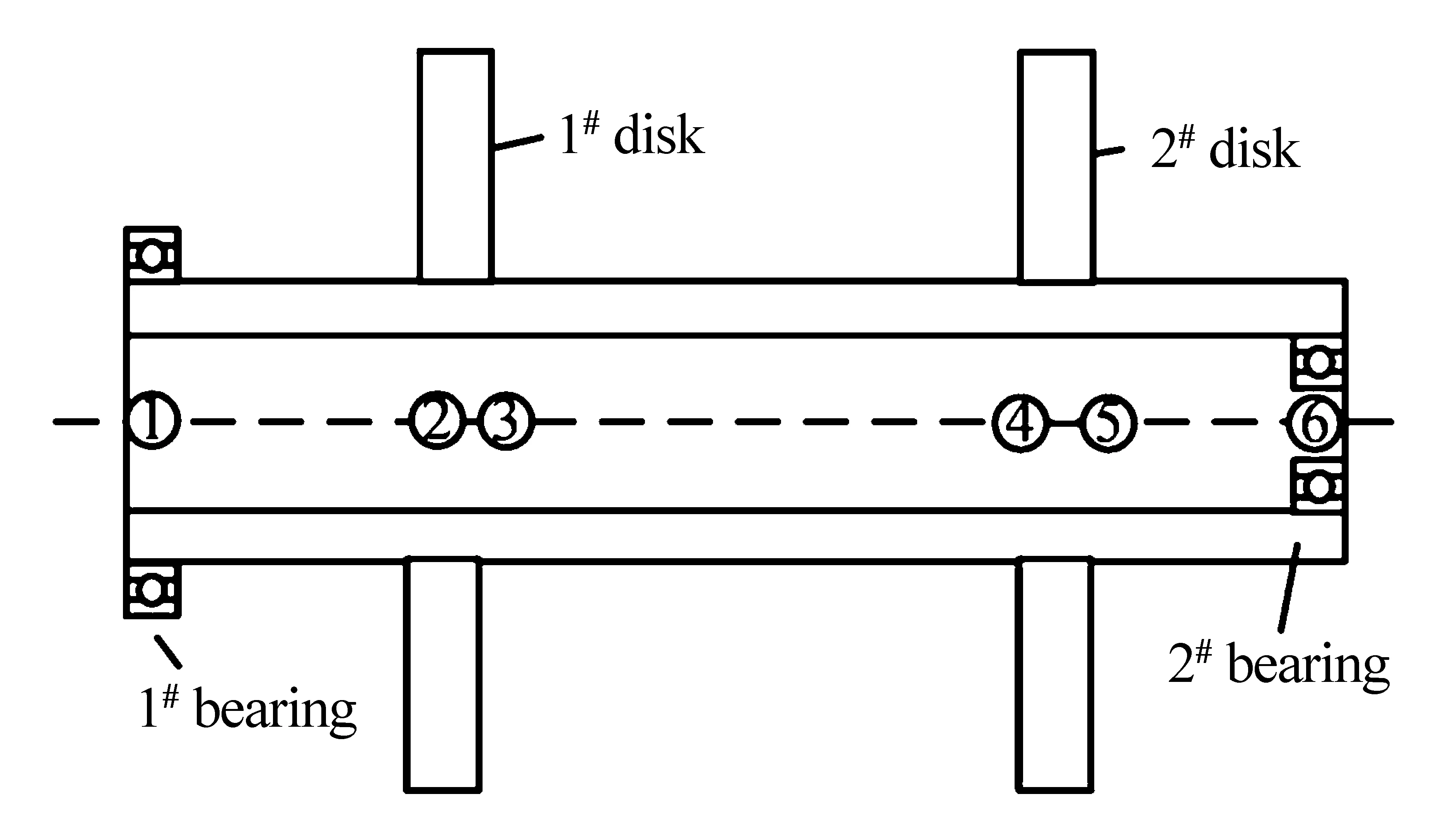
图1 高压转子滚动轴承系统模型Fig.1 Model of high pressure rotor-rolling bearing system
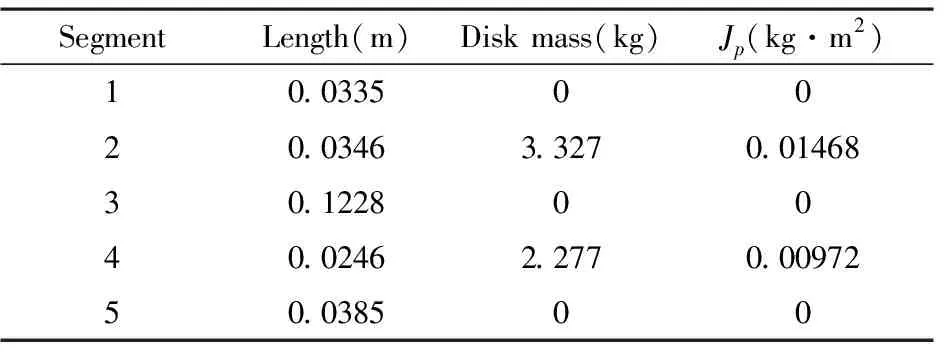
表1 航空发动机高压转子模型参数Table 1 Parameters of high pressure rotor of aero engine
转子阻尼设定为Rayleigh阻尼,如(2)所示:
C=αM+βK
(2)
式中,
ξ1和ξ2为系统前两阶模态阻尼系数;ω1、ω2为系统的一、二阶临界转速.通过计算Campbell图可得系统一、二阶临界转速分别为17212r/min、37296r/min.转子内径为0.0381m,外径为0.0508m,材料密度ρ为8304kg/m3,弹性模量E为2.069×1011Pa.
如图2,假设轴承共有Nb个滚珠,则每个滚珠在t时刻的方位角如(3):
(3)
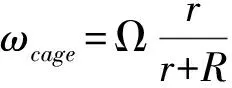
ωcage为保持架转速;R为轴承外环半径;r为轴颈半径.
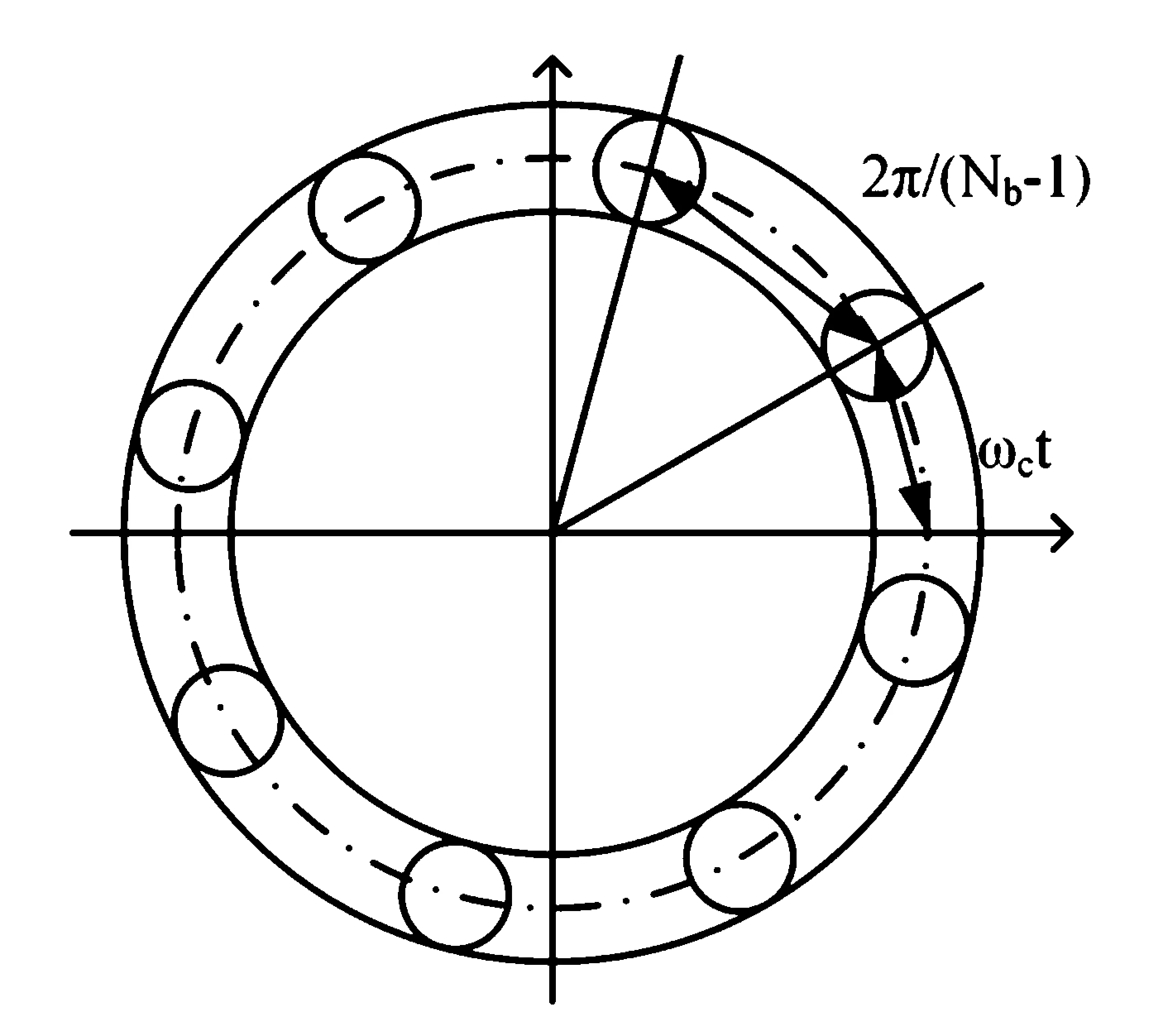
图2 滚动轴承结构简图Fig.2 Structure diagram of rolling bearing
第j个滚珠的弹性变形如(4)式所示:
δj=δj0H(δj0)
(4)
δj0=xcosθj+ysinθj-V
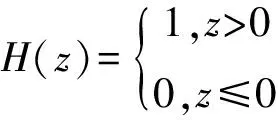
其中,V为径向游隙.
由赫兹接触理论可以求得轴承非线性力表达式[20]:
(5)
Cb为赫兹接触刚度,由滚珠与轴承内外环的材料、参数所确定.本文轴承选用6211型号轴承,参数如表2所示,由式(6),可得该轴承VC振动频率与转子工作频率比Bn为3.55.

表2 6211型滚动轴承参数Table 2 Parameters of 6211 type rolling bearing
(6)
式中,fvc为VC振动频率,fr为转子工作频率.
2 数值计算结果及分析
采用自适应步长Newmark-β直接积分法对系统非线性运动微分方程求解,Newmark-β算法的控制参数分别取0.25和0.5,采用局部误差(Local Error)作为步长调整依据,将计算结果的局部误差限制在0.75%~1%之间.为着重分析滚动轴承非线性力作用的影响,1#轴承选为6211型轴承,采用非线性力模型,而2#轴承为刚度为8.75×106N/m的轴承,计算得到该转子随转速升高的响应特性,进而针对低转速下出现的VC振动现象,计算分析了在不同转速下不平衡量与轴承游隙对VC振动的影响.
2.1 不同转速下转子动力响应分析
设定转子不平衡位于1#轮盘上,偏心距e=181μm.当轴承游隙V=20μm时,结点3在X向的振动幅频特性如图4所示,可见该转子系统的第一阶临界转速为18800r/min,与线性轴承刚度条件计算得到的一阶固有频率相接近.
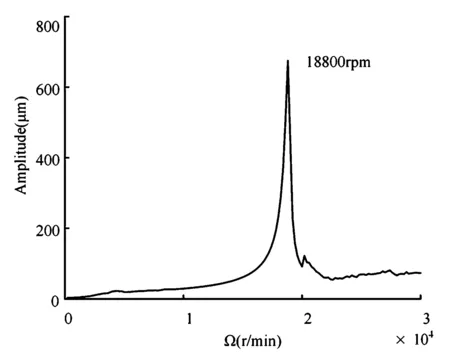
图4 幅频特性图Fig.4 Amplitude-frequency diagram
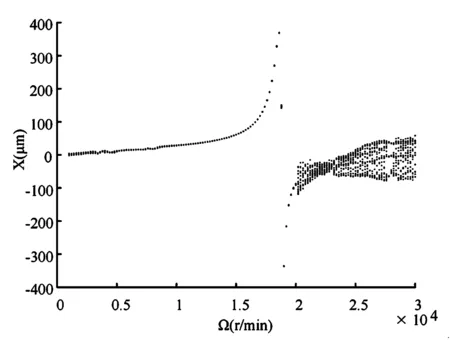
图5 分岔图Fig.5 Bifurcation diagram
由结点3处X振动响应的分岔图5可知,随着转速的升高,转子振动大致经历了三个阶段,0~10000r/min的低转速区,转子振动处于不稳定状态;10000~20000r/min的中转速区,转子振动较稳定;20000~30000r/min的高转速区,转子振动再次进入不稳定状态.
由于重力的作用,轴颈在滚动轴承内Y方向存在初始弯曲,当转子在低转速下工作时不平衡激励力很小,使得滚动轴承Y向非线性刚度高于X方向.如图6所示,结点1处在200r/min时,Y方向振幅为X方向振幅的1/16.随着转速升高,不平衡质量激励力逐渐增大,相比之下重力的作用减弱,当转速达到5000r/min时,X、Y方向振幅趋于相同,如图7所示.
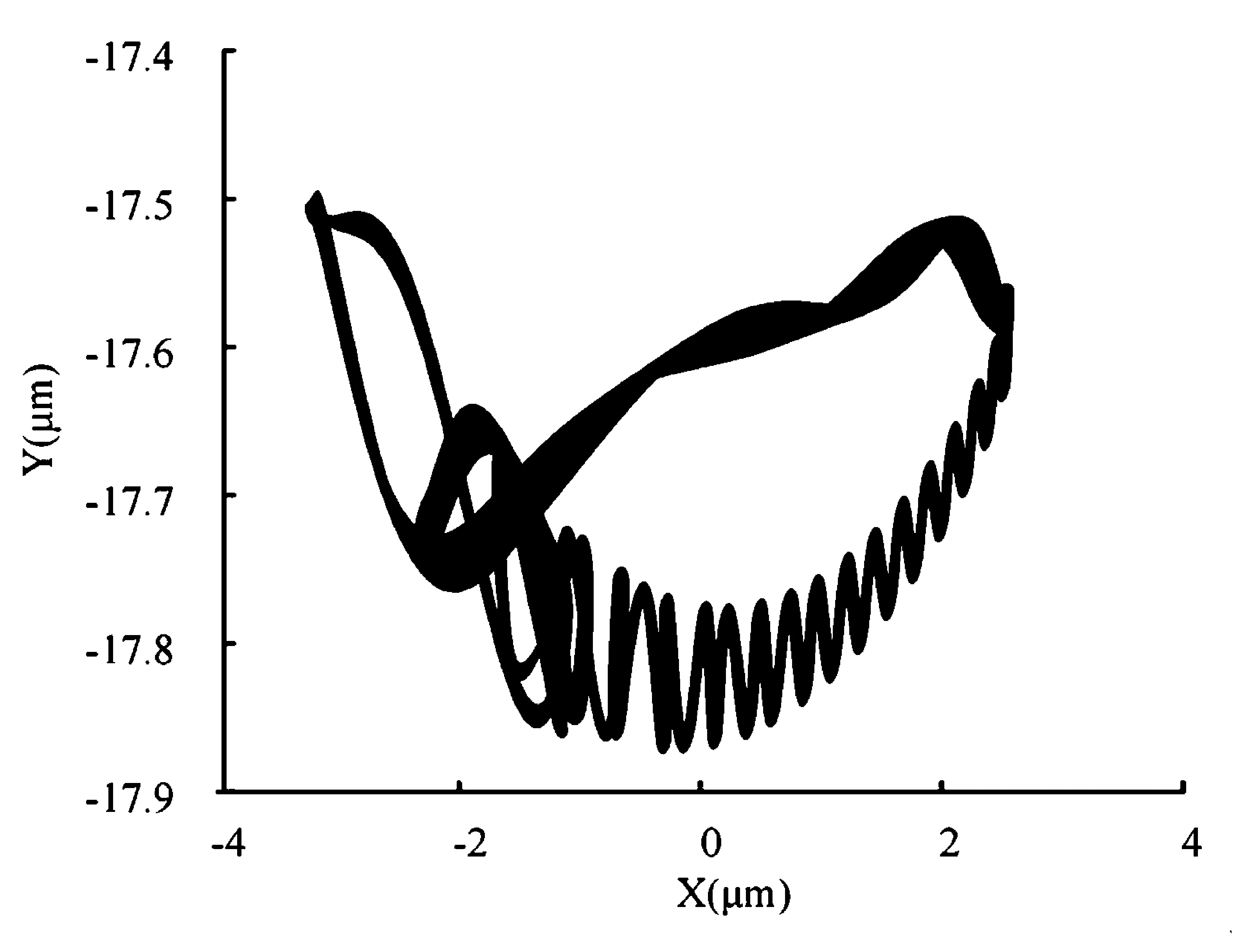
图6 轴心轨迹图(200r/min)Fig.6 Axle center trajectory diagram(200r/min)
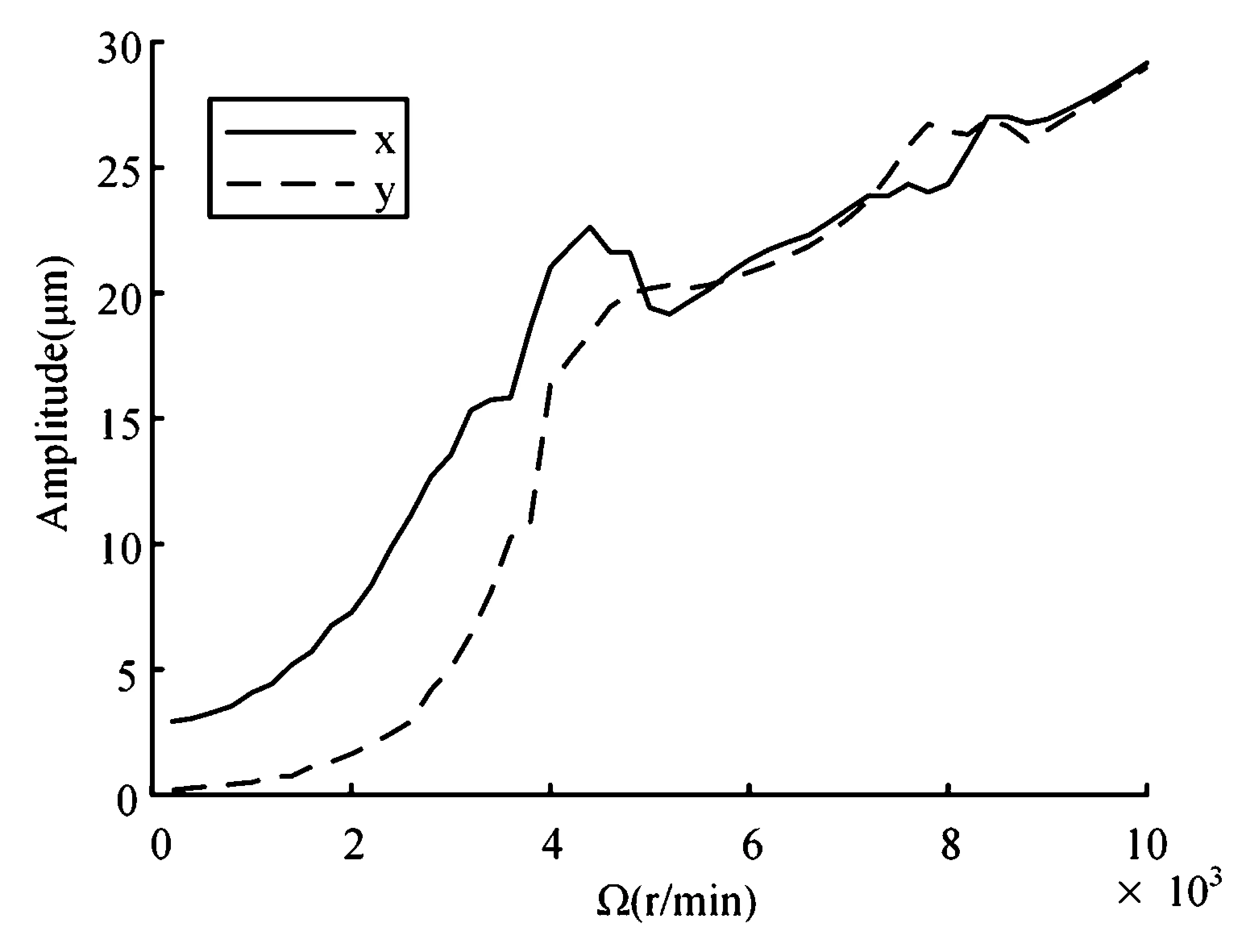
图7 幅频特性图Fig.7 Amplitude-frequency diagram
同时在转速200r/min时,模拟得到了与Mevel[16]实验测得的VC振动波形相近的计算结果,如图8(a).由图8(b)可知,fvc是fr的3.55倍,与VC振动频率的公式(6)计算结果一致.在0~1500r/min区间上,结点3在X方向响应三维谱图如图9所示,振动的频率成分主要是fvc、fr以及两者的倍频和组合频率.随着转速升高,如图10所示,X方向通频幅值Ax迅速增大,VC振动幅值Avcx逐步减小.继续升高转速,如图11,在3000~10000r/min区间内,频率成分主要包含工频fr及其倍频,Avcx已经基本消失,工频fr的倍频在转速接近10000r/min时基本消失.
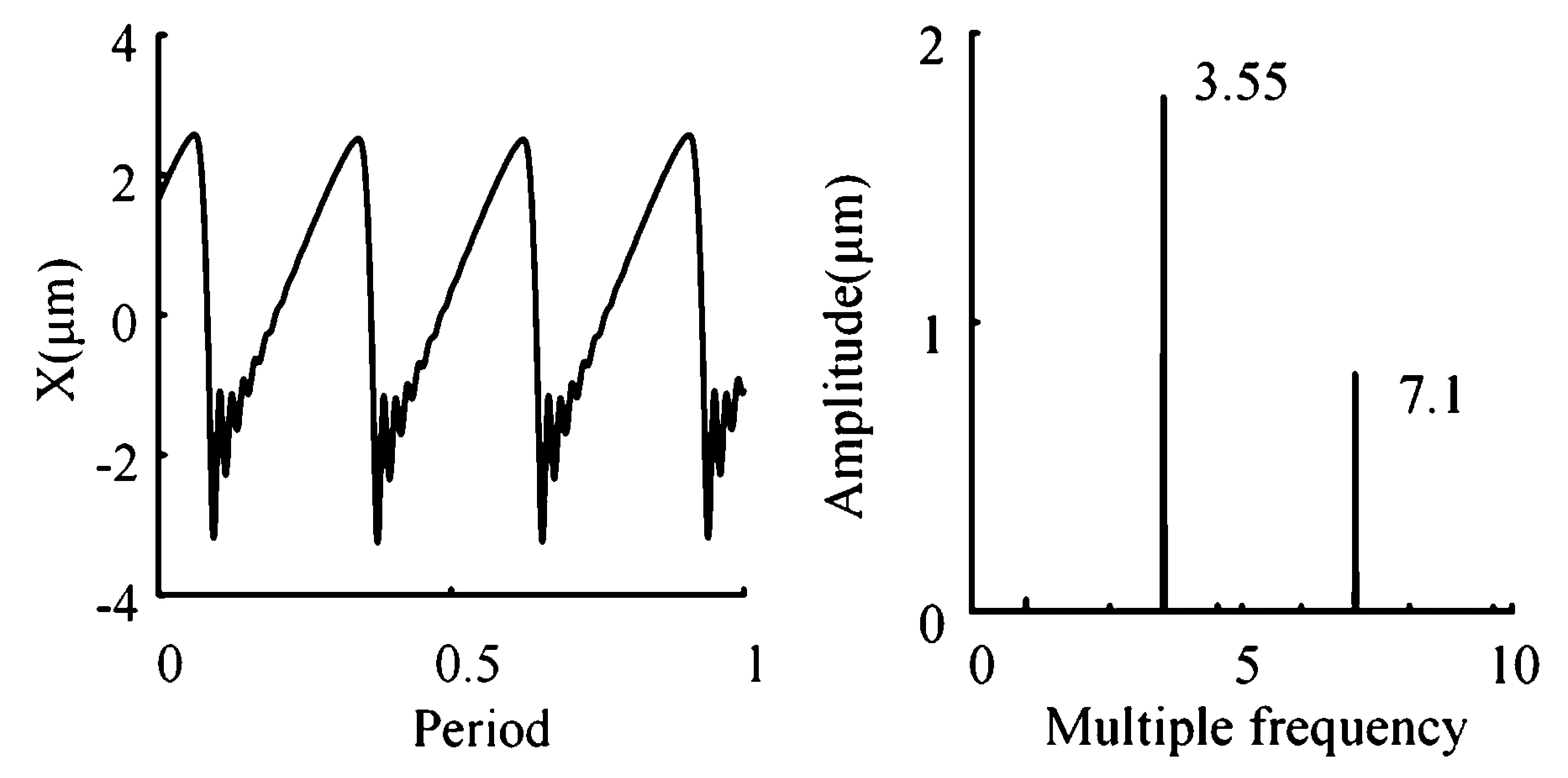
图8 时域图、频谱图(200r/min)Fig. 8 Time domain chart and spectrogram(200r/min)
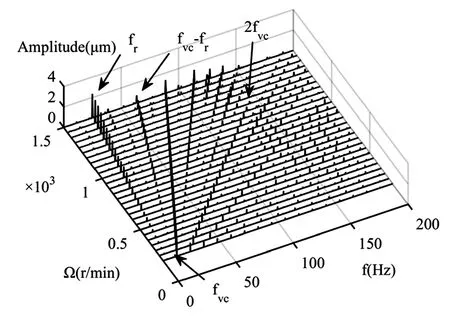
图9 三维频谱Fig.9 Waterfall of rotor′s run-up
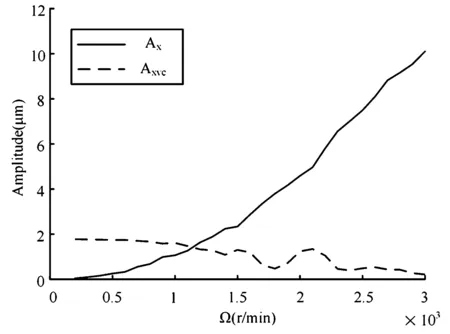
图10 Ax与Axvc幅值Fig.10 Amplitude of Axand Axvc
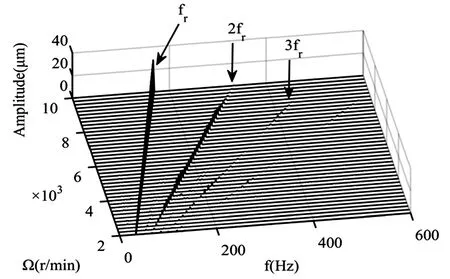
图11 三维谱图Fig.11 3D spectrogram
随着转速升高,转子振动进入稳定状态,如图5所示,响应以工频为主的同步振动,15000r/min转速结点3的轴心轨迹和X方向频谱如12所示.
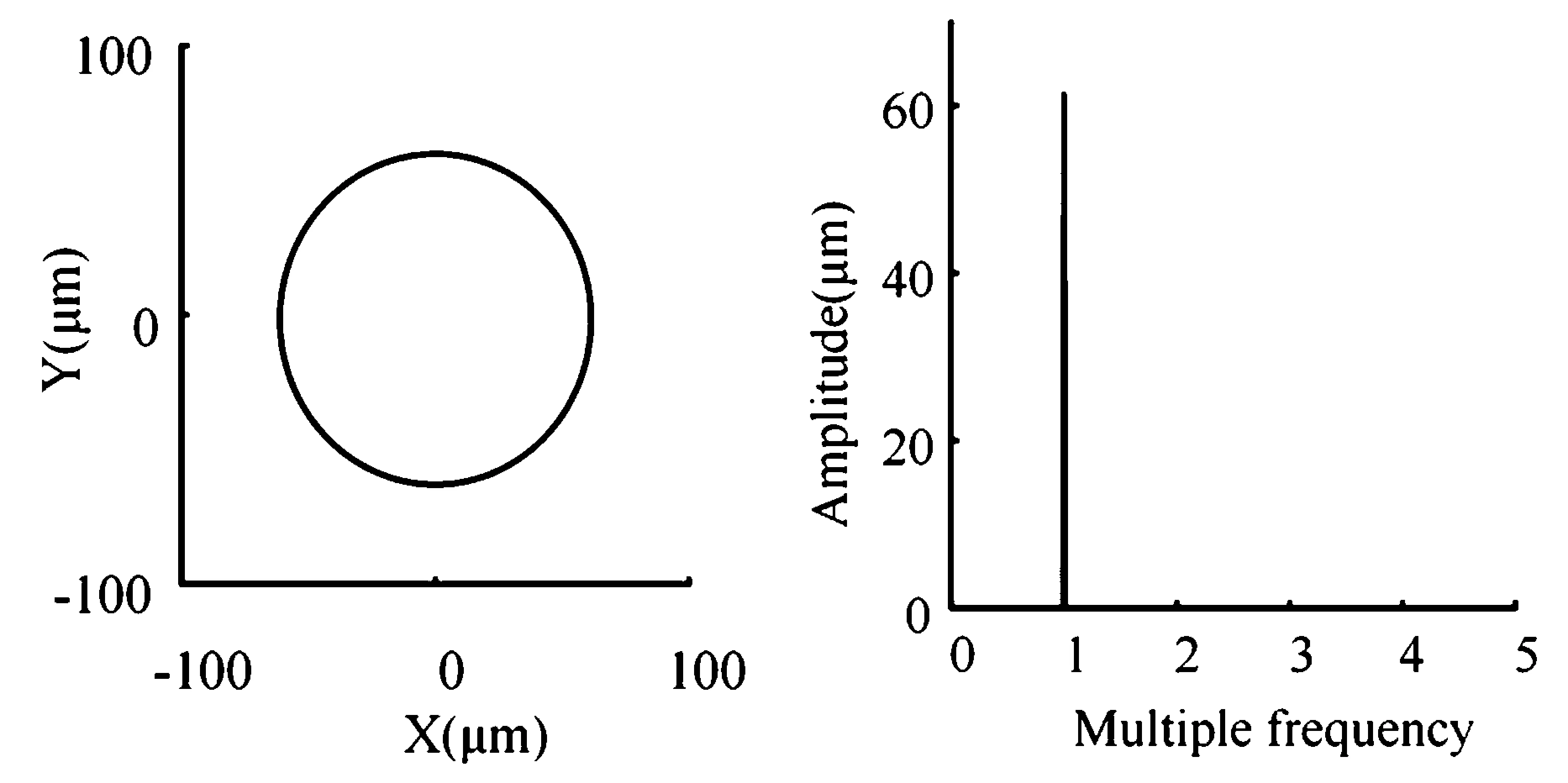
图12 轴心轨迹、频谱(25000r/min)Fig.12 Axle center trajectory diagram and spectrogram(25000r/min)
在转速20000~30000r/min区,转子振动除了工频成分之外出现了低频分量,该低频分量为转子的一阶固有频率.随着转速的升高,低频频率保持不变,出现“锁频”现象,如图13.并且转速升高工频fr谱线的幅值减小,固有频率fc分量的幅值逐渐增大.转速25000r/min时转子轴心轨迹和X向频谱如图14所示,振动响应中包括多个频率分量,而其中工频和一阶固有频率占比较大.
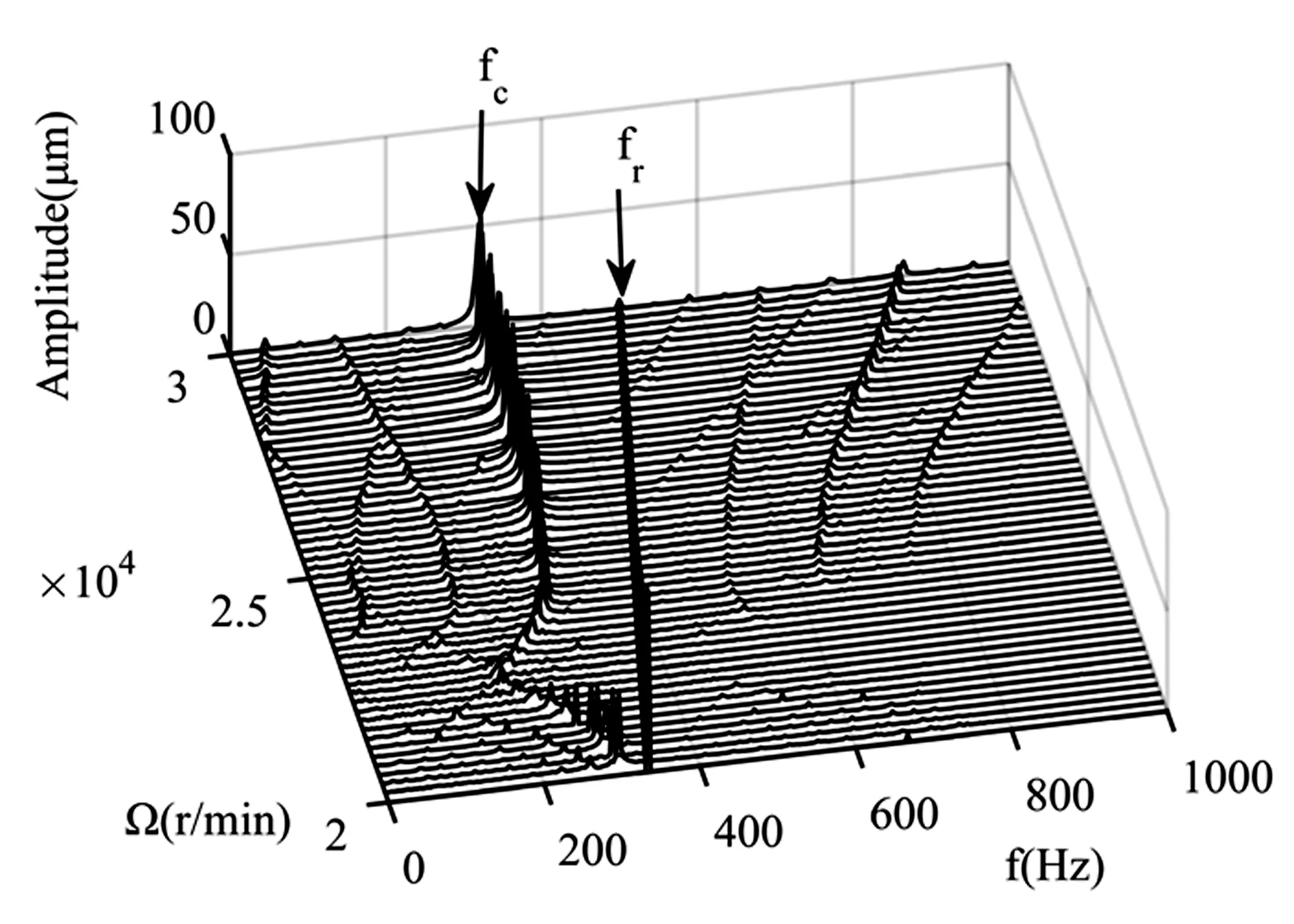
图13 三维谱图Fig.13 3D spectrogram
可见,该转子系统由于滚动轴承的非线性特性在低、中、高转速范围内呈现出丰富多样的非线性响应特征.
2.2 系统参数对VC振动的影响
除转子转速外,转子不平衡量和滚动轴承游隙是转子系统中更易改变的参数,本文分析转速、游隙与不平衡量对低转速区VC振动的影响.由于该模型转子中滚动轴承非线性力作用于结点1处,而在低转速区Y方向振动受到抑制,故采用结点1处X方向振动响应来分析.
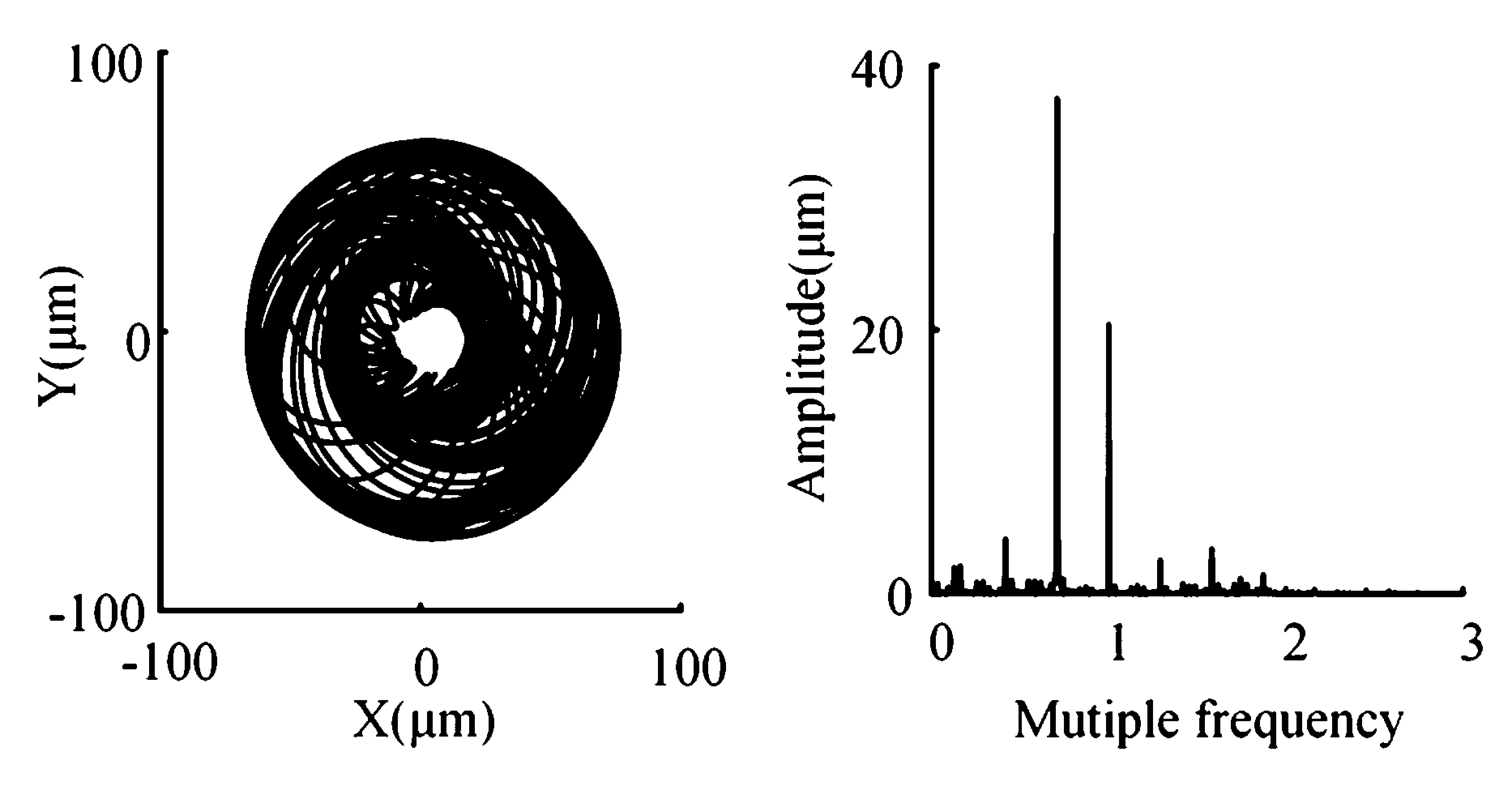
图14 轴心轨迹、频谱(25000r/min)Fig.14 Axle center trajectory diagram and spectrogram(25000r/min)
2.2.1 滚动轴承径向游隙对VC振动影响
设定转子不平衡位于1#轮盘上,偏心距e=0.181mm,轴承游隙变化范围为10~100μm,转速的变化范围为200~3000r/min.结点1处X向振动响应中VC振动频率fvc的幅值随转速和游隙变化的三维图.可见,不同的游隙条件下,随着转速升高VC振动幅值总体上呈现先减小再增大,然后再次减小的趋势规律.
讨论不同转速下VC振动幅值在游隙10~100μm条件下的变化情况,200~850r/min区间内,随着滚动轴承游隙的增大VC振动幅值不断增大;转速位于850~1600r/min区间时,在低游隙范围内VC振动幅值随着游隙增大而增大,当游隙增大至一定大小后,VC振动幅值随着游隙增大基本保持不变;而当转速高于1600r/min,VC振动基本消失,系统VC振动消失转速不受轴承游隙的影响.
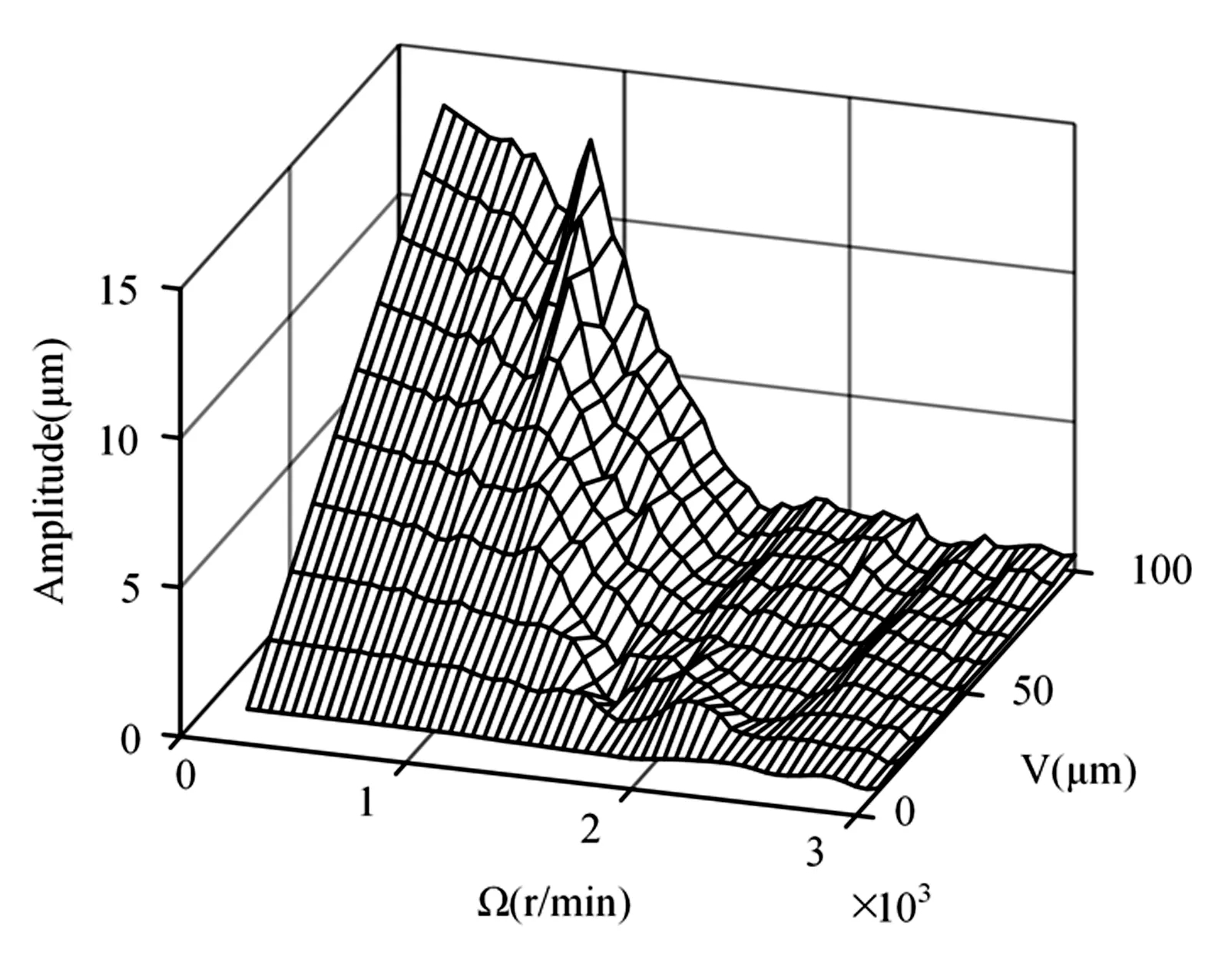
图15 fvc幅值Fig.15 Amplitude offvc
2.2.2 转子不平衡量对VC振动影响
选取滚动轴承游隙V=50μm,同样设定转子不平衡位于结点3处的1#轮盘上,偏心距e的变化范围为0.05~0.2mm,图15(a)为VC振动幅值随转速和不平衡量变化的三维谱图,可见:在不同偏心距下,VC振动幅值随转速的升高总体也呈现先减小再增大,然后再次减小直至消失的趋势特征.观察不同转速下VC振动幅值在偏心距0.05~0.2mm范围下的变化情况,转速在0~1000r/min区间时,转子VC振动幅值随着不平衡量增大却基本不变;转速高于1000r/min时,VC振动幅值随着不平衡量增大而略有降低.系统VC振动基本消失时的转速随不平衡量的增大而降低.
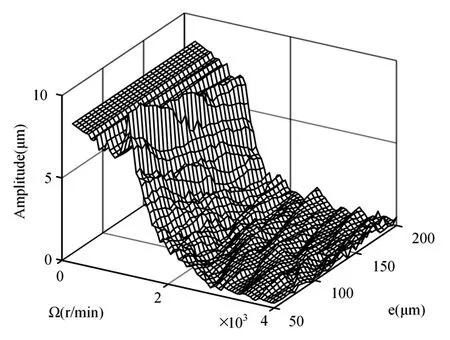
图16 fvc幅值Fig.16 Amplitude offvc
3 结论
1)建立了考虑滚动轴承非线性力的典型航空发动机高压转子-轴承系统的动力学模型,采用Newmark-β自适应步长法计算得到了低转速区转子的VC振动现象,模拟的VC振动时域波形与Mevel实验测得VC振动波形相近,验证了本文所采用的模型与算法在预测转子-滚动轴承系统振动响应中的有效性.
2)在宽广的转速范围内,利用幅频特性、分岔图、频谱图计算分析得到了该转子系统具有低转速区出现VC振动,中转速区出现同步工频振动、高转速区出现低频分量“锁频”的复杂动力学响应特征.
3)对VC振动幅值的影响参数分析表明,随转速的升高,VC振动幅值具有先减小再增大,然后再减小至基本消失这一趋势特征.增大游隙会使VC振动的幅值增大,转子不平衡量对VC振动幅值影响较小.并且,系统VC振动基本消失时的转速随不平衡量增大而降低,但基本不受轴承游隙的影响.
