动力吸振器对转子系统气流激振稳定性影响分析*
2018-03-14许琦姚红良刘子良闻邦椿
许琦 姚红良 刘子良 闻邦椿
(1.沈阳工业大学 机械工程学院, 沈阳 110870) (2.东北大学 机械工程与自动化学院, 沈阳 110819)
引言
气流激振问题是影响离心压缩机稳定运行的重要因素之一.气流激振会导致压缩机转子振动失稳、进而跳车,严重影响工业生产.因此,研究抑制转子气流激振、提高转子稳定性问题非常重要[1-3].
目前针对流体激振问题的处理方法主要有两种:一是扰乱和控制流体的流动,二是附加外力.扰乱和控制流体流动的实质为调整流体力参数[4],进而抑制其引起的振动、提高转子稳定性.典型的扰乱流体流动的方法有采用旋转迷宫密封[5]、孔型阻尼密封[6]和“反旋流”[7]等;郎骥等研究了可倾密封代替固定密封以减小气流激振[8].附加外力主要包括流体力和电磁力[9]等,常见于应用在抑制流体轴承引起的失稳振动[10,11].
吸振作为一种振动抑制方法,常用于结构振动的抑制,如抑制输液管道振动[12]和高速有砟轨道振动[13]等.目前在转子系统中也有所应用,如何立东等研究动力吸振器抑制转子临界振动[14-16];姚红良等提出永磁负刚度吸振器及非线性吸振器抑制转子在共振区附近的振动[17-19];Tehrani等利用动力吸振器抑制转子振动以防止转静子接触[20].此外,离心摆式吸振器用于抑制转子和往复振动设备的扭转振动.Parker等研究了离心摆式吸振器的模型、振动特性及稳定性[21,22];赵艳影等利用时滞动力吸振器抑制扭转振动[23].
动力吸振器抑制转子系统振动具有广阔的应用前景.目前的研究主要集中在对转子受迫振动包括不平衡及扭转振动的抑制,对流体引起转子不稳定振动抑制的研究相对较少.因此,本文采用动力吸振方法抑制压缩机转子气流激振、提高其失稳转速,通过理论分析及数值验证证实吸振器能够有效地提高转子的稳定性.
1 气流激励下转子-吸振系统动力学模型
气流激励下转子-吸振系统动力学模型如图1所示.采用单盘的简单转子模型[24];气流激励f采用Muszynska流体力模型[25],作用在圆盘上;将吸振器通过滚动轴承附加在转子上[17].转子-吸振系统的振动微分方程如下:
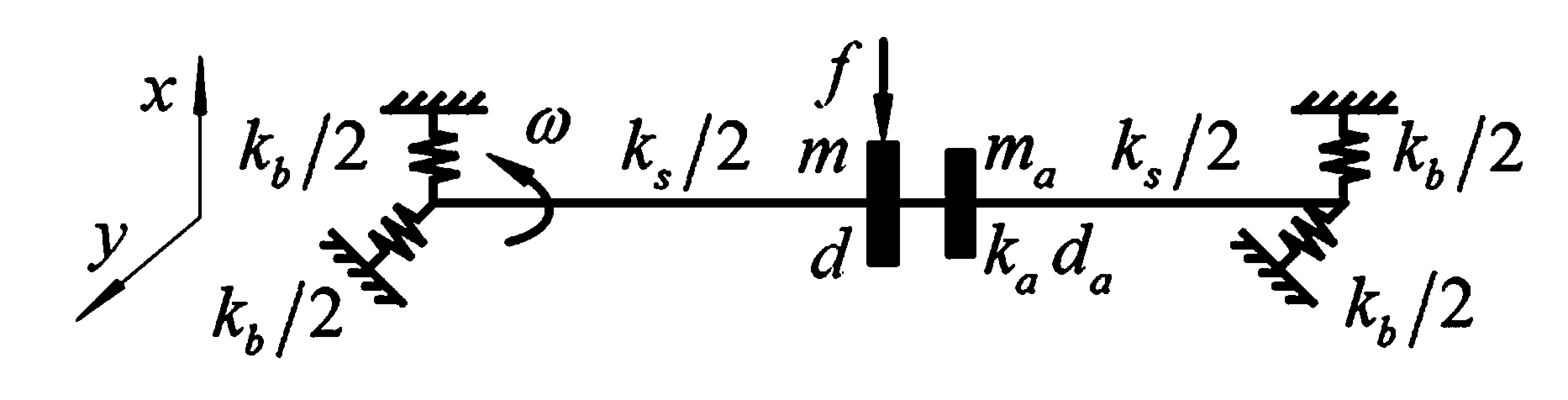
图1 转子-吸振系统模型Fig.1 The model of the rotor-fluid force system with attached the absorber
ka(X-Xa)+fX=meω2rcosωt
ka(Y-Ya)+fY=meω2rsinωt
(1)
其中,
(kf-mfω2λ2)X+ωdfλY
ωdfλX+(kf-mfω2λ2)Y
df=d0(1-U2)-n,kf=k0(1-U2)-n
式中,m、ma、mf、d、da、df和k、ka、kf分别为转子、吸振器和流体的质量、阻尼和刚度;转子刚度k中包括轴刚度ks和支承刚度kb;me和r分别为转子偏心质量和偏心距;ω为转速;λ为流体周向平均流速比;rf为间隙.
将方程(1)无量纲化:
(2)
其中,
fx=εfx″+μdx′+2εfλy′+
(μk-εfλ2)x+μfλy
fy=εfy″-2εfλx′+μfy′-
μfλx+(μk-εfλ2)y

εf=mf/m,df=d0(1-u2)-n,
kf=k0(1-u2)-n,λ=λ0(1-u)b,
2 气流激励下转子-吸振系统稳定性
考虑小振幅情况,忽略流体质量及非线性项,流体力可化简为:
fx=μdx′+μkx+μdλy
fy=μdy′-μdλx+μky
(3)
此时,转子系统方程(2)为线性方程,其非齐次方程解的稳定性等价于齐次方程零解的稳定性,故忽略偏心,根据Lyapunov第一近似理论,求解系统特征值判断其稳定性.其自由振动特征方程为:
(4)
式中,s为系统复特征值.
特征方程(4)解的表达式非常复杂,直接代入数值求解.参数如下表所示.

表1 系统参数Table 1 The parameters of the system
设
σa=ωa/ωr,σ=ω/ωr
(5)
将参数带入特征方程(4)中,取吸振器阻尼比ζa=0.05,得到气流激振下转子-吸振系统失稳转速随吸振器固有频率的变化曲线(稳定性图),如图2所示.从图2(a)中可以看出:(1)区域z1中特征值实部均小于零,此时转子系统的振动稳定、具有衰减特性;(2)蓝色实线部分表示存在一个特征值实部等于零、其他特征值小于零,此时转子系统处于临界失稳状态,其振动为谐波振动;(3)区域z2中存在一个特征值实部大于零,此时转子系统的振幅随时间以指数的形式增加,气流激励中的非线性项开始起作用,振幅增加直到形成极限环.
图2(b)中红色实线表示无吸振器时转子失稳转速[24],从图2(b)中可以看出:在转子阻尼与吸振器阻尼比值不变的情况下(此时转子无吸振器失稳转速不变),当气流激励的刚度交叉项增大时(d0增加),稳定区域z1逐渐减小,在吸振器固有频率接近转子固有频率时,附加吸振器后的失稳转速仍大于无吸振器时转子失稳转速.
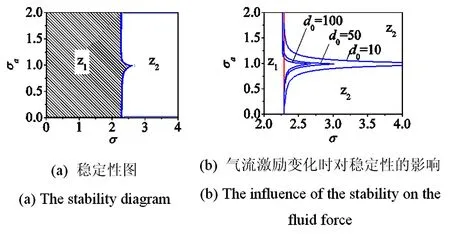
图2 气流激振下转子-吸振系统稳定性 (ζa=0.05)Fig.2 The stability diagram of the rotor-fluid force system with attached the absorber (ζa=0.05)
取吸振器固有频率等于转子固有频率,即σa=1,得到气流激振下转子-吸振系统失稳转速随吸振器阻尼比的变化曲线(稳定性图),如图3所示.图3(a)中所表达的内容与图2(a)类似,即区域z1为稳定区域、蓝色实线为临界稳定边界、区域z2为失稳区域.

图3 气流激振下转子-吸振系统稳定性 (σa=1)Fig.3 The stability diagram of the rotor-fluid force system with attached the absorber (σa=1)
从图3(b)中可以看出,在失稳区域z2中,存在一个区域z4,其特征值中存在两个大于零的实部,即存在二阶失稳频率;从图3(c)中可以看出:当气流激励的刚度交叉项增大时(d0增加),稳定区域z1逐渐减小,在吸振器阻尼比接近0.06时,转子系统附加吸振器后的失稳转速较大;从图3(d)中可以看出:随着d0增加,区域z4的边界越来越接近转子无吸振器失稳转速.
3 数值验证
采用Newmark法直接求解转子系统振动微分方程.图4为ζa=0.05时气流激振下转子-吸振系统振动响应.(1)取(σa=1, σ=2),振动响应如图4(a)所示,此时转子系统的振动稳定,具有衰减特性;(2)取(σa=1.5, σ=2.2754),振动响应如图4(b)所示,此时转子系统处于临界状态,其振动为谐波振动;(3)取(σa=0.5, σ=2.5),振动响应如图4(c~e)所示,转子振幅先增加后平稳,频谱中存在两个离散的频率:气流激励引起的频率及转频,Poincaré截面为一个封闭图形,此时转子系统为拟周期失稳.

图4 当ζa=0.05时气流激振下转子-吸振系统振动响应Fig.4 The time domain responses of the rotor-fluid force system with attached the absorber (ζa=0.05)
图5为σa=1时气流激振下转子-吸振系统振动响应.(1)取(ζa=0.4, σ=2),振动响应如图4(a)所示,此时转子系统的振动稳定,具有衰减特性;(2)取(ζa=0.2, σ=2.3820),振动响应如图4(b)所示,此时转子处于临界稳定状态,其振动为谐波振动;(3)取(ζa=0.5, σ=3),振动响应如图4(c~e)所示,转子振幅先增加后平稳,频谱中存在两个离散的频率:气流激励引起的频率及转频,Poincaré截面为一个封闭图形,此时转子系统为拟周期失稳;(4)取(ζa=0.02, σ=3),振动响应如图4(f~h)所示,转子振幅先增加后平稳,频谱中存在两个离散的频率:气流激励引起的二阶失稳频率及转频,Poincaré截面为一个封闭图形,此时转子系统为拟周期失稳.
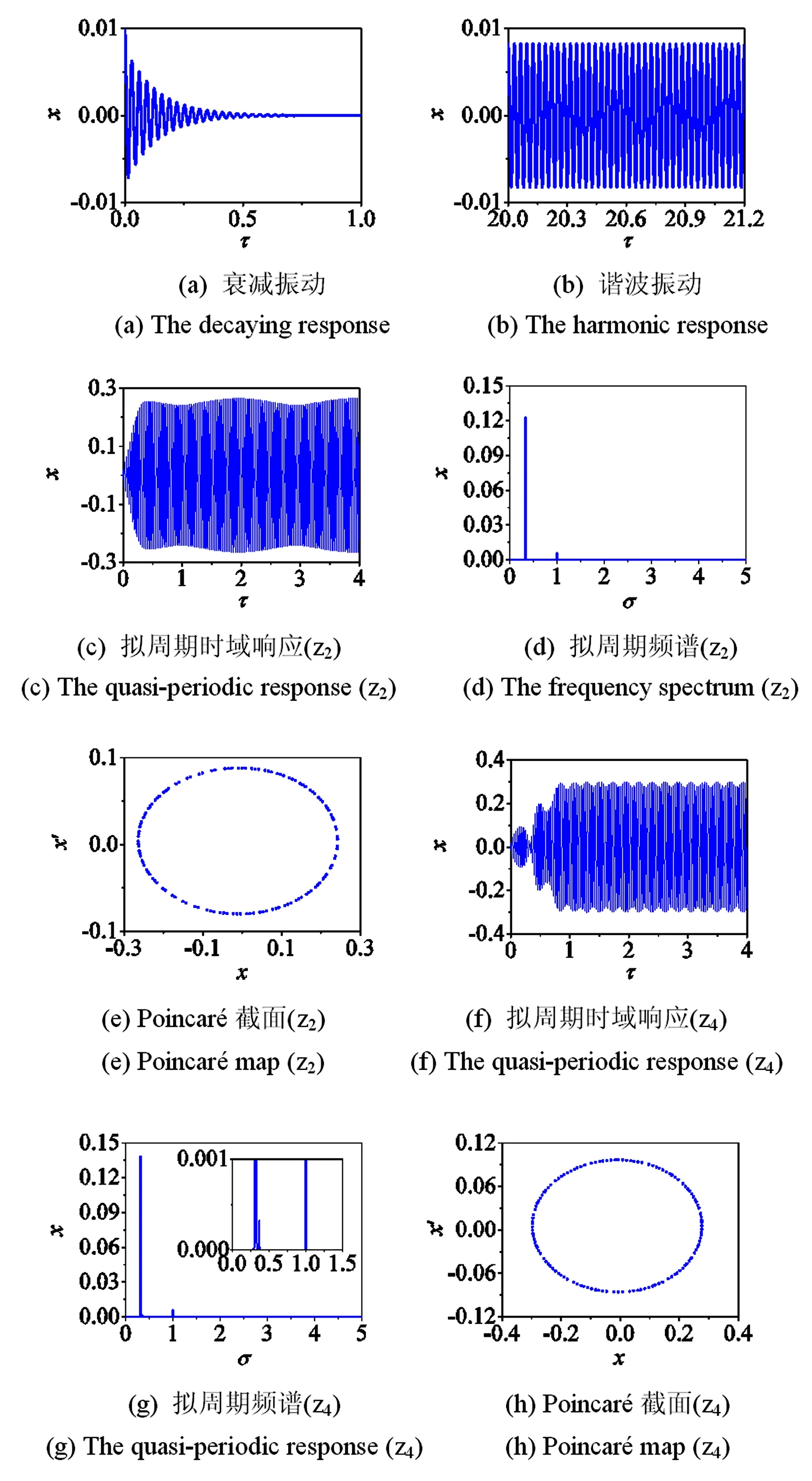
图5 当σa=1时气流激振下转子-吸振系统振动响应Fig.5 The time domain responses of the rotor-fluid force system with attached the absorber(σa=1)
4 结论
将吸振器附加到转子系统中,研究气流激励作用下转子-吸振系统的稳定性,分析吸振器系统参数对转子稳定性的影响,并进行了数值验证.结果表明:
1)附加吸振器能够有效地提高转子系统的稳定性;
2)吸振器固有频率及阻尼比对转子系统稳定性有较大的影响,分析结果表明在吸振器固有频率接近转子固有频率及吸振器阻尼比在0.06附近时转子具有较高的失稳转速;
3)附加吸振器后,在一定的参数条件下,气流激励作用下转子系统存在二阶率失稳现象,原因即附加吸振器后增加了原转子系统自由度,失稳频率接近转子-吸振系统的二阶固有频率.
