抗差自适应UKF算法在地基光学跟踪空间目标中的应用

刘光明, 徐帆江

(中国科学院软件研究所天基综合信息系统重点实验室, 北京 100190)

0 引 言

空间目标跟踪定轨技术是空间目标监视系统应用的基础,在当今航天精确定轨领域,改进测控设备的测控精度并且提高空间目标的轨道确定精度是研究热点[1-2]。抗差自适应滤波算法的处理流程为[3-4]:如果观测值存在异常,就根据抗差估计原则对值进行处理;如果动力学模型发生误差,则对模型的各个分量使用自适应的方法进行调节,或者将模型当作整体,使用统一的自适应因子的方法改变模型对状态参数的影响[5]。非线性滤波是空间目标实时跟踪的有效方法之一[6],在实时跟踪任务中,测量异常值(野值)的存在可能导致目标跟踪误差突增甚至丢失,文献[6]讨论了实时定轨的抗差估计方法,针对无迹卡尔曼滤波(unscented Kalman filter,UKF)算法在未知时变噪声下出现的滤波精度下降或者发散的问题。文献[7]在其基础上提出了SPRHKF算法,此算法对模型的瞬时干扰误差和不确定性具有一定的鲁棒性。上述算法虽然在不同程度上改进了UKF算法的自适应能力,但是仍然存在一些不足[8-9]:算法普遍存在计算复杂并且引入其他限制条件而导致难以工程实现的问题,另外虽然解决了UKF算法的发散问题,但是其收敛性较差,例如对初始状态误差要求尽可能小[10]。对于传统UKF算法在跟踪滤波的过程中由于噪声统计特性时变的影响而出现滤波精度下降乃至发散的问题,本文提出了新的抗差自适应UKF算法,该算法基于极大后验估计,仿真实例结果验证了算法在不同条件下的有效性和可行性。

1 目标观测模型

地面站对空间非合作目标的观测几何如图1所示。由于仅有一个跟踪目标的观测平台,每个时刻对应的观测方程都是非正定的。所以需要使用轨道动力学模型求解目标轨道,使用在观测时间序列中测量的数据进行计算,实际处理时多使用基于轨道动力学的滤波算法[11]。

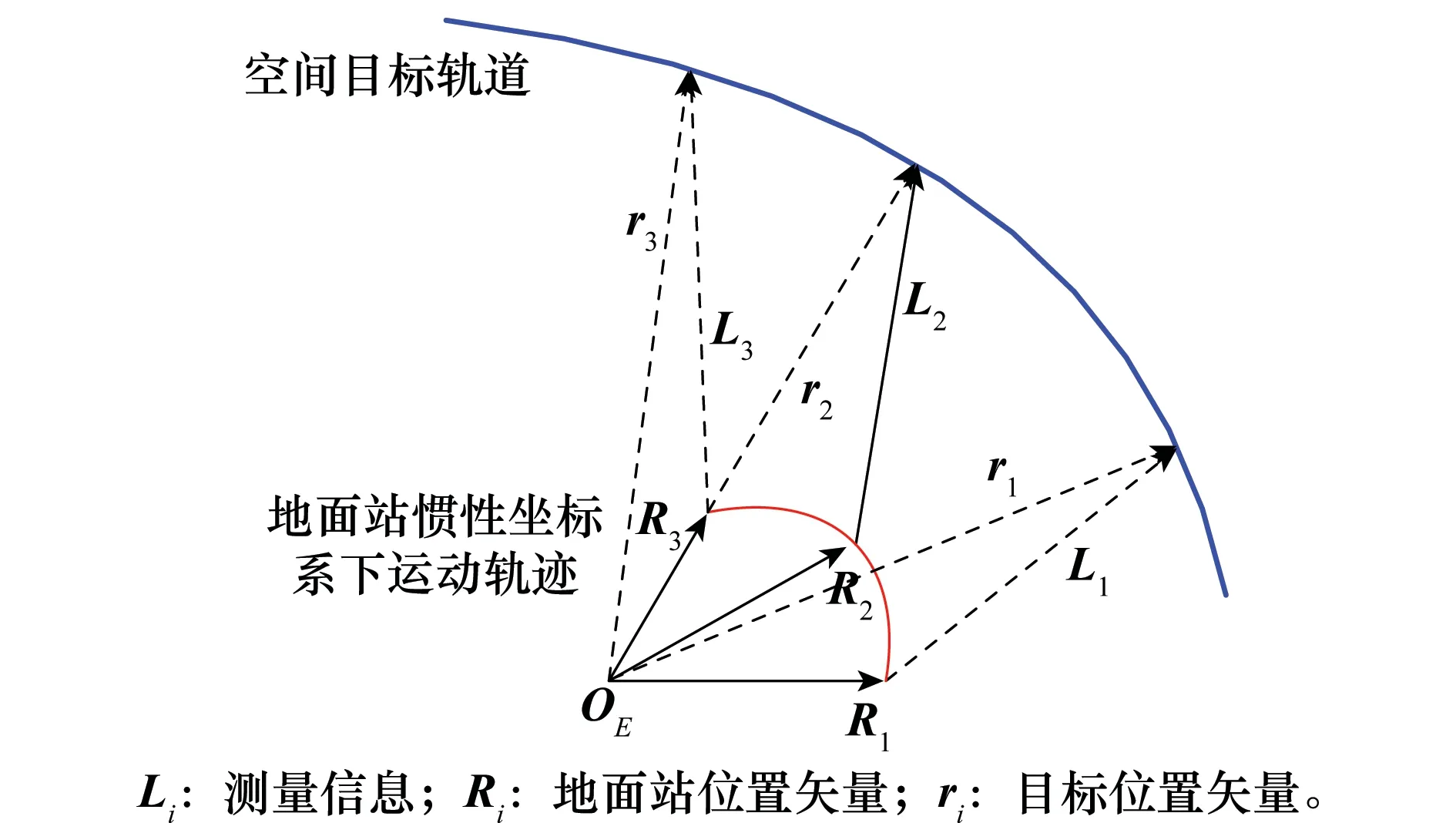
图1 地面站对空间非合作目标的观测几何Fig.1 Observation geometry of ground station to space non cooperative target

地基光学测角跟踪中,观测平台获得空间目标的测角信息(赤经β、赤纬ε),赤经和赤纬可以由J2000地心惯性坐标系下目标位置矢量r=[x,y,z]T和地面站位置矢量R=[X,Y,Z]T确定[12]。

(1)

则观测矢量Y=[β,ε]T可以表示为状态矢量X=[rT,RT]T的非线性函数：

Y=H(X)+v

(2)

式中,v为测量噪声矢量。

2 目标跟踪系统模型

一段观测时间序列下,构造目标状态转移函数xk=f(xk-1),目标的角度测量序列为yk,则可建立地面站对空间非合作目标的光学测角跟踪模型[13]为

(3)

设离散非线性随机系统(3)中的wk和vk是互不相关的非零均值高斯白噪声,且具有时变统计特性[14]，即

(4)

式中,Qk是非负定对称的过程噪声的协方差矩阵;Rk是正定对称的观测噪声的协方差矩阵。

设初始状态x0与wk、vk互不相关,服从高斯正态分布,其均值和协方差矩阵[15]为

(5)

所以要解决的问题就是在量测噪声和系统噪声的统计特性时变或者未知的情况下,基于角度测量值yk设计具有噪声统计估计器的抗差自适应UKF算法,计算目标位置速度矢量。

3 带时变噪声统计特性估计器的抗差自适应UKF算法

定理1根据极大后验估计理论[16],在满足式(4)和式(5)的情况下具有时变噪声统计特性的次优极大后验估计公式为

(6)

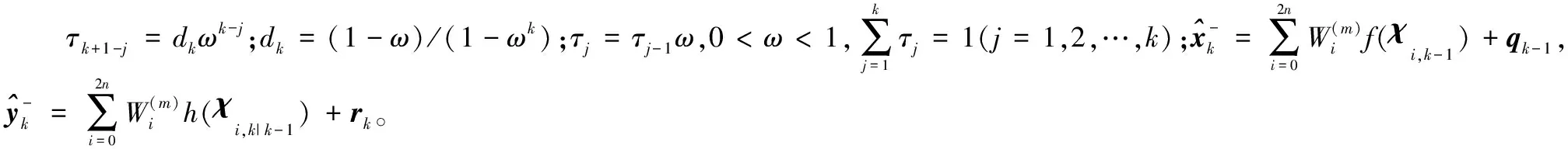
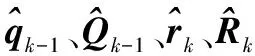
J=p[qk-1,Qk-1,rk,Rk,Xk|Yk]=

p[Yk|qk-1,Qk-1,rk,Rk,Xk]·

p[Xk|qk-1,Qk-1,rk,Rk]p[qk-1,Qk-1,rk,Rk]/p[Yk]

(7)

由假设知时变噪声wk、vk相互独立,为方便推导,不妨暂时设wk、vk具有常值统计特性:E[wk]=q,Cov[(wk-qk)(wj-qj)T]=Qδkj,E[vk]=r,Cov[(vk-rk)(vj-rj)T]=Rδkj,则根据条件概率分布密度的乘法定理[17],可得

A1·|P0|-1/2·|Q|-k/2·

(8)

(9)

从而,有

J=A1·A2·|P0|-1/2·|Q|-k/2·|R|-k/2·

{p[qk-1,Qk-1,rk,Rk]/p[Yk]}·

A·|Q|-k/2|R|-k/2·

(10)

式中

A=A1·A2·{p[qk-1,Qk-1,rk,Rk]/p[Yk]}·

为常数项。

J和lnJ极值相同,式(10)可改写为

(11)

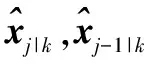
(12)

(13)

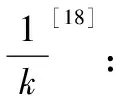
(14)

(15)

(16)

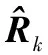
(17)

类似地有

(18)

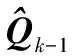
(19)

证毕

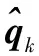
(20)

进而有

(21)

(22)

具体计算步骤如下:

步骤1滤波初始化

步骤2计算Sigma样本点

式中,(P)i表示取矩阵P的第i行;

步骤3时间更新

χi,k|k-1=f(χi,k-1)

步骤4量测更新

yk|k-1=h(χj)

Kk,j=Pxkyk(Pvkvk)-1

步骤5计算抗差自适应因子βk[20]

βk=

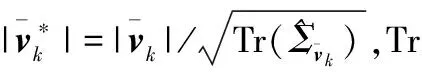
步骤6再次进行量测更新

4 抗差自适应UKF算法流程

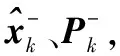
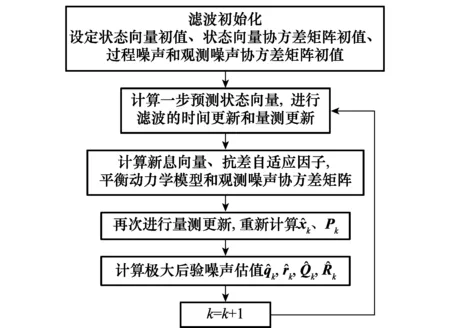
图2 抗差自适应UKF算法流程图Fig.2 Flowchart of robust adaptive UKF algorithm

5 仿真实验与分析

设地基观测站Station的大地坐标为:北纬40.1°、东经116.2°、高程0.8 km,空间目标SatT的轨道根数如表1所示,星历时间为2016年1月1日12:00:00。

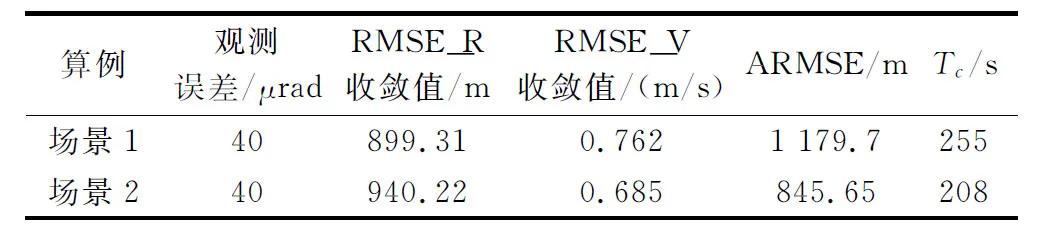
表1 空间目标的轨道根数

利用STK模拟生成了作为标称轨道的空间目标运行轨道。另外,滤波器的轨道预报模型和标称轨道计算模型都只考虑非球形J2、J3、J4项摄动,以对比检验本文提出的抗差自适应UKF算法的性能。设仿真时长为Ta=5 000 s,滤波周期Ts=2 s,N表示滤波点数,蒙特卡罗仿真次数取M=50次。数值实验中,观测数据中加入粗差,噪声统计特性q、Q、r、R未知且Q时变。仿真结果评价指标采用误差均方根(root mean square error,RMSE)、平均误差均方根(average root mean square error,ARMSE)及收敛时间Tc。

设初始状态误差为[5 km 5 km 5 km 1 m 1 m 1 m],观测数据误差取40 μrad。其中,常值系统误差为10 μrad,随机误差为30 μrad,则有r=[10-510-5],R=diag[9×10-109×10-10];加入的过程噪声统计特性为q=[50 50 50 0 0 0],Q=diag[10210210210-610-610-6]。仿真过程中，在t=3 800 s和t=4 000 s时观测数据中加入400 μrad的粗差,在t=3 200 s后,过程噪声统计协方差阵为Q=diag[1.5×1041.5×1041.5×10410-610-610-6]。

设置初始观测噪声均值和协方差矩阵分别为:r0=[0 0],R0=diag[10-1010-10],过程噪声均值和协方差矩阵分别为:q0=[0 0 0 0 0 0],Q0=diag[1 1 1 10-610-610-6]。

本文设计2个场景。场景1:Station对SatT采用普通UKF算法进行跟踪滤波;场景2:Station对SatT采用抗差自适应UKF算法进行跟踪滤波，引入抗差自适应因子,初值设为1,构造自适应因子采用的常量k0=1.3,k1=6.0,遗忘因子ω=0.95。仿真结果如图3～图6和表2所示。

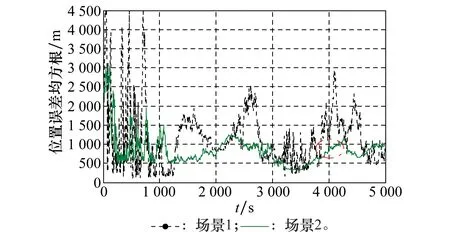
图3 位置误差均方根的比较Fig.3 Comparison of the root mean square of position error

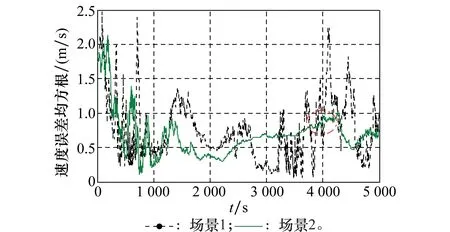
图4 速度误差均方根的比较Fig.4 Comparison of the root mean square of velocity error

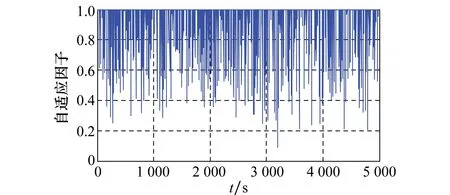
图6 抗差自适应UKF的自适应因子变化曲线(场景2)Fig.6 Adaptive factor change curve of robust adaptive UKF (Case 2)

由以上仿真结果可知:

(1) 在t=3 200 s前，即过程噪声的协方差矩阵还没有改变前,UKF算法的非线性滤波效果正常,但是在收敛时RMSE_R和RMSE_V曲线振荡较大,并且收敛时间也相对较长，Tc=255 s。当过程噪声的协方差矩阵改变后,UKF算法逐渐失效,其滤波精度的振荡降低甚至有发散的趋势。特别是在t=3 800 s和t=4 000 s时观测数据中加入粗差后,振荡幅值快速增大,RMSE_R最高达到2 900 m,RMSE_V最高达到2 m/s。尽管经过一段时间误差曲线的振荡幅值逐渐收窄,但是极易受到扰动影响而出现发散。

(2) 抗差自适应UKF可以克服过程噪声协方差阵时变和观测异常的问题,其RMSE_R和RMSE_V的收敛值最终分别保持在940.22 m和0.685 m/s,并且振荡幅值很小,具有较高的稳定性。

(3) 由图5可知,抗差自适应UKF在t=3 200 s后,观测噪声的均值的模和协方差阵的矩阵范数分别阶跃到了0.7×10-4和5×10-8附近振荡,说明抗差自适应UKF将过程噪声协方差阵时变影响通过时变噪声统计估计器传递到了观测噪声的统计特性估计上,提高了滤波过程中状态向量估计的稳定性。

(4) 由图6可知，抗差自适应UKF的自适应因子在滤波整个阶段都在频繁调整,并且对过程噪声协方差阵的时变性更为敏感。自适应因子在t=3 200 s时降低到0.1,调整幅值相对最大,这也在一定程度上减轻了时变噪声统计估计器的工作负担。自适应因子在观测异常时自身幅值调整并不明显,这与观测粗差不算太“恶劣”有一定关系,或者说抗差自适应UKF的自适应因子主要在于整体上提高滤波对观测异常和状态扰动的抵制能力。

6 结 论

传统UKF算法的滤波精度高于扩展卡尔曼滤波算法,但在滤波前需已知噪声的先验统计特性[21]。由于在地面站对空间非合作目标的光学测角跟踪滤波实际应用中,噪声先验信息一般未知或者不准确,即使已知但却有时变性,会使传统UKF算法的滤波精度下降乃至发散。提出基于极大后验估计的抗差自适应UKF算法,将抗差自适应因子和时变噪声统计特性在线估计相结合,解决了传统UKF在噪声统计未知时变下滤波性能不佳的问题, 且有抵制观测异常和模型扰动的能力。仿真结果表明，该算法可以在未知噪声先验统计的情况下,在线估计未知时变噪声的统计特性,对噪声变化具有一定的自适应能力,使用的抗差自适应因子可以控制跟踪滤波的稳定性。

[1] KONG Q, GUO J, SUN Y, et al. Centimeter-level precise orbit determination for the HY-2A satellite using DORIS and SLR tracking data[J]. Acta Geophysica, 2017,65(1):1-12.

[2] JU B, GU D, HERRING T A, et al. Precise orbit and baseline determination for maneuvering low earth orbiters[J]. GPS Solutions, 2017, 21(1):53-64.

[3] ZHANG L, YIN X, NING Z, et al. Robust filtering for a class of networked nonlinear systems with switching communication channels[J].IEEE Trans.on Cybernetics,2017,47(3):671-682.

[4] ABOLHASANI M, RAHMANI M. Robust Kalman filtering for discrete-time systems with stochastic uncertain time-varying parameters[J]. Electronics Letters, 2017, 53(3):146-148.

[5] MAJUMDER R, SADHU S. Robust extended Kalman filter for ballistic object tracking during re-entry[C]∥Proc.of the IEEE India Conference, 2017:1-6.

[6] GAO N, WANG M Y, ZHAO L. A novel robust Kalman filter on AHRS in the magnetic distortion environment[J]. Advances in Space Research, 2017: 201-209.

[7] SONG Q, HAN J D. An adaptive UKF algorithm for the state and parameter estimation of a mobile robot[J]. Acta Automatica Sinica, 2008, 34(1): 72-79.

[8] JULIER S J, UHLMANN J K. Unscented filtering and nonlinear estimation[J]. Proceedings of the IEEE,2004,92(3):401-422.

[9] KHALID S S, REHMAN N U, ABRAR S. Robust stochastic integration filtering for nonlinear systems under multivariate t-distributed uncertainties[J].Signal Processing,2017,140(4):53-59.

[10] BEIDAGHI S, JALALI A A, SEDIGH A K, et al. RobustH∞, filtering for uncertain discrete-time descriptor systems[J]. International Journal of Control Automation and Systems,2017,15(3):995-1002.

[11] HAM B, CHO M, PONCE J. Robust guided image filtering using nonconvex potentials[J].IEEE Trans.on Pattern Analysis and Machine Intelligence,2017:2070-2077.

[12] JIA B, PHAM K D, BLASCH E, et al. Cooperative space object tracking using space-based optical sensors via consensus-based filters[J]. IEEE Trans.on Aerospace and Electronic Systems, 2016, 52(4):1908-1936.

[13] JIA B, BLASCH E, PHAM K D, et al. Space object tracking and maneuver detection via interacting multiple model cubature Kalman filters[C]∥Proc.of the IEEE Aerospace Conference, 2015:1-8.

[14] CHEN C, LI S, QIN H, et al. Real-time and robust object tracking in video via low-rank coherency analysis in feature space[J]. Pattern Recognition, 2015, 48(9):2885-2905.

[15] WEN X, ZHANG X W, ZHU Y P. Design of fault detection observer based on hyper basis function[J]. Tsinghua Science and Technology, 2015, 20(2):200-204.

[16] WAN P, CHEUNG G, FLORENCIO D, et al. Image bit-depth enhancement via maximum-a-posteriori estimation of AC signal[J]. IEEE Trans.on Image Processing, 2016, 25(6):2896-2909.

[17] YU T, LAI Y H. Generalized maximum a posteriori, spectral amplitude estimation for speech enhancement[J]. Speech Communication, 2016, 76(C):112-126.

[18] QUINTANA D, GARCARODRGUEZ S, CINCOTTI S, et al. Combining RMT-based filtering with time-stamped resampling for robust optimization[J]. International Journal of Computational Intelligence Systems, 2015, 8(5):874-885.

[19] 赵琳, 王小旭, 孙明, 等. 基于极大后验估计和指数加权的自适应UKF滤波算法[J]. 自动化学报, 2010,36(7):57-61.

ZHAO L, WANG X X, SUN M, et al. Adaptive UKF filtering algorithm based on maximum a posterior estimation and exponential weighting[J]. Automatica Sinica,2010,36(7):57-61.

[20] SNIEKERS S, VAART A V D. Adaptive Bayesian credible sets in regression with a Gaussian process prior[J].Statistics,2015,9(2): 1504-1512.

[21] 刘光明. 基于天基测角信息的空间非合作目标跟踪算法及相关技术研究[D]. 长沙:国防科技大学, 2011.

LIU G M. Non-cooperative space target tracking algorithm based on angular measurement information and related technology[D].Changsha: National University of Defense Technology,2011.