基于形变模型的空间阵列位置误差估计方法
2018-03-14霍立寰廖桂生杨志伟
霍立寰, 廖桂生, 杨志伟
(西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071)
0 引 言
从20世纪60年代中期以来,随着空间科学技术的飞速发展,空间阵列[1]在卫星通信、空间探索、地球观测等方面得到广泛应用。空间阵列沿轨道运行时,遭遇的周期性冷热交变和较大的温度梯度将造成空间阵列变形,造成的阵元误差严重影响雷达系统性能,尤其对于多通道阵列处理,明显减弱杂波抑制效果和降低动目标检测能力[2],因此有必要提出有效的适合空间阵列的误差校正算法。
目前,针对空间阵列形变误差的研究主要集中在形变阵列的方向图分析[3-7]、阵元位置的测量与补偿[8-11]及阵列形变对信号处理影响[12-14]3个方面。文献[9]利用卫星上的探针天线观测阵面,通过比较阵面形变前后的测量结果,最后对每个阵元的相位误差进行补偿;文献[10]通过在天线板上放置多个测温传感器,结合地面热真空实验得到的大量数据来估计阵元位置误差并进行电补偿处理;美国空军研究实验室和喷气推进实验室合作开发的L波段大孔径星载雷达,通过天线上搭建的自动校准和计量系统,对阵元的空间位置进行持续测量[11]。
空间阵列的位置误差校正问题本质上为阵列误差的校正问题,在不同的条件和背景下提出多种校正方法[15-21]。其中最典型的是文献[15-16]基于子空间原理,提出的基于联合迭代求解的经典算法,简称WF算法。该算法实现简单且不需要辅助信源,虽然具有较高的校正精度,但是容易产生局部收敛,并且对于线阵的估计存在模糊[22-23],在实际应用中无法达到理想的效果。针对方位依赖的阵元误差,文献[21]等提出阵列校正的辅助阵元法,通过引入少量精确校正的辅助阵元,实现阵列误差进行无模糊联合估计,但是由于星载系统的限制,辅助阵元的实现较困难。
针对空间阵列的位置误差问题,提出基于形变模型的误差估计方法。该方法首先根据初始位置采用多重信号分类(multiple signal classification, MUSIC)算法估计角度,然后通过对代价函数进行泰勒一阶近似,最小化代价函数得到阵元位置初步估计;再利用形变模型,对初步估计的位置采用总体最小二乘法获得形变模型参数,并且根据形变模型对阵元位置进行优化,更新阵元位置继续迭代直到代价函数收敛。本文算法具有快速收敛和高精度的优点,并且在低信噪比情况下仍具有良好的稳健性。
1 信号模型
在空间环境中,星载平面阵列受到各种载荷的作用发生复杂的形变。空间阵列由各子板构成,复杂的形变退化到三维的抛物柱面,能够用抛物柱面进行描述,如图1所示。

图1 面阵抛物柱面形变模型Fig.1 Parabolic cylindrical distortion model of the planar array
考虑由M×N个阵元组成二维阵列,并以第一个阵元(参考阵元)为坐标原点,理想阵面为XY平面建立直角坐标系。阵元(m,n)的实际坐标定义为(xmn,ymn,zmn),理想坐标定义为(xmn0,ymn0,zmn0),满足
(xmn,ymn,zmn)=(xmn0,ymn0,zmn0)+(Δxmn,Δymn,Δzmn)
(1)
Dx、Dy分别为阵列在X轴、Y轴上孔径长度,zmax为抛物柱面的最大形变量,因此抛物柱形变曲面上的坐标(x,y,z)满足
(2)
假设有K个远场窄带信号sk(t)入射到该二维阵列,中心波长为λ,入射角为(θk,φk),其中k=1,2,…,K。方位角θk为入射信号投影到XY平面后与X轴的夹角,俯仰角φk为其与Z轴的夹角。实际阵列的输出向量为
(3)
式中,n(t)是加性噪声向量;a(θk,φk)是(θk,φk)方向的实际阵列导向矢量,表示为
a(θk,φk)=[1,…,e-j2πdmn,K/λ,…,e-j2πdMN,K/λ]T
(4)
式中
dmn,k=xmncosθksinφk+ymnsinθksinφk+zmncosφk
将式(3)表示成矩阵形式为
X(t)=A(θ)S(t)+n(t)
(5)
式中,A(θ)的第k列为a(θk,φk);S(t)的第k个元素为sk(t)。
实际接收数据的协方差矩阵为
(6)
对R进行特征值分解,其最小的MN-K个特征值所对应的特征向量un(n=K+1,K+2,…,MN)组成噪声子空间Un=[uK+1,uK+2,…,uMN]。
实际中阵列协方差矩阵由有限次快拍数据来估计,即
(7)
式中,x(l)表示第l次快拍数据;L为快拍数。
2 位置误差自校正方法
2.1 传统WF方法原理
传统WF算法[16]是同时估计角度和位置误差的联合迭代算法。该方法首先利用子空间正交原理构造代价函数式(8);然后通过位置误差的一阶泰勒级数展开为式(9)形式,将耦合的位置误差与来波角分离,进而根据估计的角度计算得到位置误差;最后将角度和位置进行联合迭代,通过最小化代价函数直至收敛得到误差估计结果。
(8)


(9)
2.2 基于形变模型的位置误差估计
WF求解阵元位置时,没有利用阵面结构约束,对空间阵列形变导致的阵元位置误差估计结果精度较差。考虑到空间阵列形变引起的位置误差具有相关性,因此在每一次迭代后,所提方法对解得的位置根据形变模型进行约束,进而得到修正的阵元位置。阵元位置优化方法如下。
依据抛物柱面形变模型,设
可得
yρ=z
(10)

考虑到阵元位置在每一维都存在位置误差,因此利用总体最小二乘法来实现最优的曲面拟合效果,ρ的总体最小二乘解为
(11)

(12)
估计出阵列形变参数后,结合形变模型对阵元位置进行修正,解决优化问题,即
(13)
基于形变模型的阵元位置误差估计方法步骤如下:


步骤3初始化:设迭代次数l=0,根据各个阵元的理想位置构造空间谱为
(14)

(15)

步骤5对求得的阵元位置进行总体最小二乘拟合形变模型参数,并代入式(13)进行优化,解得修正后的阵元位置估计;
步骤6计算代价函数值Ql并判断收敛条件是否满足,若Ql-Ql-1>ε,则返回步骤4继续迭代,并令l=l+1,否则结束迭代。
算法流程图如图2所示。

图2 算法流程图Fig.2 Flow diagram of proposed algorithm
3 仿真实验
3.1 验证算法有效性实验
通过仿真实验,对比本文方法和传统WF算法对形变阵列的误差估计结果,验证本文方法的有效性。采用二维平面阵,阵元数M=32,N=32,入射信号波长λ=0.3 m,理想阵面在行和列均等间隔放置,间距d=0.5λ,阵列形变最大值zmax=0.25λ。由于实际中存在微小的随机机械误差,因此附加上在±0.01d范围内均匀分布的位置扰动误差。3个远场窄带信号分别θ1=30°、φ1=20°,θ2=60°、φ2=70°和θ3=100°、φ3=45°到达阵列,信噪比为20 dB,采样数为200,迭代次数为30。
根据仿真参数,对阵元位置列向取平均后的估计结果如图3所示,代价函数随迭代次数变化情况如图4所示。

图3 阵元位置估计结果Fig.3 Estimation result of the sensor positions

图4 代价函数随迭代次数变化Fig.4 Cost function versus iteration number
由图3和图4可知,传统WF算法得到的阵元位置明显有很大的偏差;基于形变模型的方法能够得到精确的估计结果。结合图4中两种方法的代价函数随迭代次数的变化关系可知,传统WF算法虽然能估计出较准确的导向矢量,但是由于没有考虑形变阵列的结构特点,不能得到实际位置结果估计。本文方法根据形变模型对阵元位置进行修正,能够得到准确的阵元位置估计值。
为便于性能比较,定义平均阵元位置误差为位置估计结果的性能指标,用符号poserror表示为
(16)
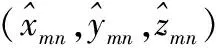
两种方法的平均阵元位置误差随迭代次数的变化关系如图5所示,两种方法的三维空间谱估计曲线如图6所示。

图5 阵元位置误差随迭代次数变化Fig.5 Sensor position errors versus iteration number

图6 三维空间谱比较Fig.6 Comparison of the three-dimensional spatial spectra
由图5和图6可知,初始的平均阵元位置误差约为33%,利用WF算法校正时平均阵元位置误差在30次迭代后约为25,利用本文方法校正时在12次迭代后即可收敛至0.43%(波长0.3 m时,对应0.65 mm);WF算法角度估计结果为
θ1=32.0°,φ1=20.4°
θ2=60.1°,φ2=70.4°
θ3=99.9°,φ3=45.8°
基于形变模型方法的角度估计结果为
θ1=30°,φ1=20.1°
θ2=60°,φ2=70°
θ3=100°,φ3=45°
仿真结果表明:对于形变阵列,WF算法对阵元位置和波达角不能得到正确的位置和角度估计结果;本文算法在实现快速收敛的同时,能够得到正确的角度估计值和高精度阵元位置估计结果。
3.2 信噪比影响实验
传统WF算法对形变天线的误差估计偏差较大,仿真对比辅助阵元法[21]与本文算法在低信噪比情况下的估计性能。实验中采用列向取平均后的阵列,最大形变量zmax=0.1λ,蒙特卡罗实验次数100,其他仿真参数与上个实验相同,只是改变信源的信噪比。平均阵元位置估计误差和角度估计均方根误差随信噪比的变化关系分别如图7和图8所示。

图7 阵元位置估计误差曲线Fig.7 Sensor position errors versus SNR

图8 角度估计均方根误差曲线Fig.8 RMSE of direction angles versus SNR
由图7和图8可知,在低信噪比的情况下,辅助阵元法性能下降严重;而基于模型的方法在信噪比低于5 dB时,平均阵元位置估计误差的估计结果在5%以内,同时能够得到高精度的角度估计,表明在低信噪比情况下,所提算法对于位置误差和角度估计具有良好的稳健性。
4 结 论
在实际工作环境中,空间阵列受热载荷等因素的影响产生形变,导致阵元位置误差严重影响雷达系统性能。提出基于形变模型的阵元位置误差估计方法,在迭代过程中根据模型参数逐步修正估计结果。仿真结果表明该方法能够快速收敛,并且在低信噪比情况下能够实现优于二十分之一波长的位置估计精度,满足高分辨空间谱估计要求。
[1] IMBRIALE W A. Space antenna handbook[M]. New York: Wiley, 2012.
[2] MELVIN W L. A STAP overview[J]. IEEE Aerospace and Electronic Systems Magazine, 2004, 19(1): 19-35.
[3] WANG H S C. Performance of phased-array antennas with mechanical errors[J]. IEEE Trans.on Aerospace and Electronic Systems, 1992, 28(2): 535-545.
[4] ZAITSEV E, HOFFMAN J. Phased array flatness effects on antenna system performance[C]∥Proc.of the International Symposium on Phased Array Systems and Technology, 2010: 121-125.
[5] SONG L, DUAN B, ZHENG F, et al. Performance of planar slotted waveguide arrays with surface distortion[J]. IEEE Trans.on Antennas and Propagation, 2011, 59(9): 3218-3223.
[6] 陈杰, 周荫清. 星载SAR相控阵天线热变形误差分析[J]. 北京航空航天大学学报, 2004, 30(9): 839-843.
CHEN J, ZHOU Y Q. Ambiguity performance analysis of spaceborne SAR with thermal mechanism errors in phased array antenna[J]. Journal of Beijing University of Aeronautics and Astronautics, 2004, 30(9): 839-843.
[7] 王从思, 康明魁, 王伟. 基于阵面变形误差的有源相控阵天线电性能分析[J]. 电子学报, 2014, 42(12): 2520-2526.
WANG C S, KANG M K, WANG W. On coupled structural-electromagnetic model of active phased array antennas with array plane structu ral distortion errors[J]. Acta Electronica Sinica, 2014, 42(12): 2520-2526.
[8] PETERMAN D, JAMES K, GLAVAC V. Distortion measurement and compensation in a synthetic aperture radar phased-array antenna[C]∥Proc.of the International Symposium on Antenna Technology and Applied Electromagnetics and the American Electromagnetics Conference, 2010:1-5.
[9] TAKAHASHI T, NAKAMOTO N, OHTSUKA M, et al. On-board calibration methods for mechanical distortions of satellite phased array antennas[J]. IEEE Trans.on Antennas and Propagation, 2012, 60(60): 1362-1372.
[10] PITZ W, MILLER D. The TerraSAR-X satellite[J]. IEEE Trans.on Geoscience and Remote Sensing,2010,48(2):615-622.
[11] MCWATTERS D, FREEDMAN A, MICHEL T, et al. Antenna auto-calibration and metrology approach for the AFRL/JPL space based radar[C]∥Proc.of the Radar Conference,2004: 21-26.
[12] PIERRO R S, PARKER S E, SCHNEIBLE R, et al. SBR waveform and processing parameters as a function of array distortion[C]∥Proc.of the Aerospace Conference, 2006: 1-15.
[13] OSSOWSKA A, KIM J H, WIESBECK W. Influence of mechanical antenna distortions on the performance of the HRWS SAR system[C]∥Proc.of the International Geoscience and Remote Sensing Symposium,2007: 2152-2155.
[14] ZULCH P, HANCOCK R, MCKAY J. Array deformation performance impacts on a LEO L-band GMTI SBR[C]∥Proc.of the Aerospace Conference,2005: 2171-2179.
[15] WEISS A J, FRIEDLANDER B. Eigenstructure methods for direction finding with sensor gain and phase uncertainties[J]. Circuits Systems and Signal Processing, 1990, 9(3):271-300.
[16] WEISS A J, FRIEDLANDER B. Array shape calibration using eigenstructure methods[J]. Signal Processing, 1991, 22(3): 251-258.
[17] LIU A, LIAO G, ZENG C, et al. An eigenstructure method for estimating DOA and sensor gain-phase errors[J]. IEEE Trans.on Signal Processing, 2011, 59(12): 5944-5956.
[18] LIU Z M, ZHOU Y Y. A unified framework and sparse bayesian perspective for direction-of-arrival estimation in the presence of array imperfections[J]. IEEE Trans.on Signal Processing, 2013, 61(15): 3786-3798.
[19] 王鼎, 吴瑛. 阵元位置误差自校正的累量域辅助阵元法[J]. 系统工程与电子技术, 2010, 32(7): 1357-1364.
WANG D, WU Y. Cumulants-based instrumental sensors method for self-calibration of sensor position errors[J]. Systems Engineering and Electronics, 2010, 32(7): 1357-1364.
[20] 杨志伟, 廖桂生. 基于最小二乘的阵元位置误差校正及性能分析[J]. 系统工程与电子技术, 2007, 29(2): 167-169.
YANG Z W, LIAO G S. Linear array position calibration based on least squares fitting and performance analysis[J]. Systems Engineering and Electronics, 2007, 29(2): 167-169.
[21] 王布宏, 王永良, 陈辉, 等. 方位依赖阵元幅相误差校正的辅助阵元法[J]. 中国科学:技术科学, 2004, 34(8): 906-918.
WANG B H, WANG Y L, CHEN H, et al. Array calibration of angularly dependent gain and phase uncertainties with carry-on instrumental sensors[J].Science in China (Series E), 2004,34(8):906-918.
[22] HUNG E K L. A critical study of a self-calibrating direction-finding method for arrays[J]. IEEE Trans.on Signal Processing, 1994, 42(2): 471-474.
[23] PIERRE J, KAVEH M. Experimental performance of calibration and direction-finding algorithms[C]∥Proc.of the Acoustics,Speech and Signal Processing, 1991:1365-1368.
