非均匀噪声背景下的欠定DOA估计方法
2018-03-14吴晨曦王可人
吴晨曦, 张 旻, 王可人
(国防科技大学电子对抗学院, 安徽 合肥 230037)
0 引 言
波达方向(direction of arrival, DOA)估计是阵列信号处理研究的重要内容,在雷达、无线通信以及电子对抗等领域有着广泛的应用。常规的空间谱估计方法[1-2]均是在背景噪声为高斯白噪声假设下进行研究的。然而在实际应用中,由于天线阵列未得到校准、接收信道的硬件差异以及非期望干扰等因素的存在,统计特性未知的相关色噪声会常常出现。当实际噪声模型不满足高斯白噪声时,传统的高分率方法的性能恶化,导致估计偏差增大、角度分辨率下降等。一般情况下,相关色噪声的协方差矩阵结构未知,但在某些特定情况下,可近似将相关色噪声进一步简化,如稀疏阵列,即假定各阵元间的噪声是不相关的空间白噪声,噪声只对阵列协方差矩阵主对角线上的元素有贡献,噪声协方差矩阵为一对角阵,但各阵元的噪声功率不相等,且各阵元噪声不相关,称为非均匀噪声[3-4]。
针对非均匀白噪声背景下的DOA估计问题近年来也受到广泛的关注[3-13],其主要思路是在某些限制条件下(如需要知道部分噪声信息、阵元数要大于信号数的3倍等)对噪声协方差矩阵进行估计并进行白化处理后,基于子空间算法获得信号的DOA信息。文献[12]针对相干信号,提出了基于空间平滑的DOA估计方法,首先通过迭代运算得到噪声协方差矩阵,消除噪声对阵列协方差矩阵的影响,然后利用空间平滑技术恢复协方差矩阵的秩,最后利用子空间方法实现DOA估计。文献[13]首先通过求和平均运算消除噪声对接收数据的影响,然后提出基于加权L1范数稀疏重构方法实现DOA估计。该方法的优点在于无需估计噪声协方差矩阵和预先知道入射信号数。然而这些方法往往牺牲了巨大的阵列孔径,使得信号环境必须要满足超定条件(即信号个数要少于阵元数),随着现代电磁环境的日益复杂,辐射源多、分布密度广,这一条件并不一定得到满足,欠定(信号数多于阵元数)DOA估计问题越来越常见。因此,针对非均匀噪声下欠定DOA估计问题的研究具有重要的现实意义。
最近,为了提高阵列利用率,嵌套阵列[14]及互质阵列[15]作为新型的稀疏阵列技术被提出,为解决欠定DOA估计问题提供了崭新的思路,其具有易于构造、阵列扩展性好、物理阵元和虚拟阵元具有解析表达式等优点受到广泛关注和研究[16-23]。文献[22]结合嵌套阵列提出基于协方差矩阵稀疏重构的DOA估计方法,该方法首先对协方差矩阵进行预白化处理以消除非均匀噪声的影响,然后将其转化为基于L1范数的稀疏重构问题进行求解,其缺点在于所有未知的入射信号DOA必须准确位于事先划分好的离散字典网格上,而实际情况下该条件并不一定满足。当入射信号的DOA未准确落在字典网格上即存在网格失配问题时,算法的估计性能会急剧下降。另一方面,虽然更密集的网格有助于减小重构误差提高估计精度,但过度密集的字典网格会使得字典的原子相关性显著增加,不能保证字典满足约束等容条件(restricted isometry property, RIP)[24]。
针对上述问题,本文以互质阵列为基础研究了基于全变分范数最小化的DOA估计方法,用于解决非均匀噪声背景下的欠定DOA估计问题。相对现有方法,该方法并不需要进行预白化处理,通过在代价函数中利用全变分范数和L1范数惩罚项分别对角度的稀疏性和噪声项进行约束,有效避免了传统稀疏重构DOA估计方法中由于角度离散化所导致的模型不匹配对估计性能的影响。
1 互质阵列模型
互质阵列结构如图1所示,其由两个不同阵元间距的均匀线阵组成。其中,子阵1的阵元数为N,间距为Md;子阵2的阵元数为2M,间距为Nd。以子阵1的第1个阵元为参考阵元,则总阵元数为2M+N-1,阵元位置集合为
U={nMd,n=0,1,…,N-1}∪
{mNd,m=1,2,…,2M-1}

图1 互质阵列结构示意图Fig.1 Structure of coprime array
假设K个远场窄带平面波信号分别以[θ1,θ2,…,θK]入射到该互质阵列上,t时刻阵列接收数据可表示为
X(t)=A(θ)S(t)+N(t)
(1)
式中,X(t)=[x1(t),x2(t),…,x2M+N-1(t)]T为阵列输出数据向量;N(t)=[n1(t),n2(t),…,n2M+N-1(t)]T为噪声向量;信号向量为S(t)=[s1(t),s2(t),…,sK(t)]T;A(θ)=[a(θ1),a(θ2),…,a(θK)]为(2M+N-1)×K维的阵列流型矩阵,其中a(θi)=[1,e-j2πMdsinθi/λ,…,e-j2π(2M-1)Ndsinθi/λ]T为入射角θi的导向矢量,λ为入射信号波长。
假设各入射信号之间互不相关,则协方差矩阵可表示为
R=E[X(t)XH(t)]=ARsAH+Q
(2)
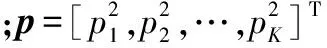
2 非均匀噪声下的欠定DOA估计
2.1 基于差联合阵列的数据预处理
首先给出差联合阵列的概念[25],定义集合D为
D={xi-xj},xi,xj∈U
(3)
式中,U表示阵元的位置集合;xi,xj表示不同阵元的位置。D表示所有阵元位置差所构成的集合,由于集合D中会存在相同的元素,定义集合D中不同的元素所构成的集合为差联合阵列,记为Du。 集合Du中元素du在集合D中出现的次数定义为权重系数w(du),差联合阵列Du中是正数的元素数目为阵列可提供的自由度,其直接决定了最多可估计信号数。
由于差联合阵列与阵列可得到的波程差是一一对应的。因此,可根据差联合中虚拟阵元的分布情况来构造出扩展的虚拟均匀线阵输出数据。对于如图1所示的互质阵列,当背景噪声为非均匀噪声时,阵列输出协方差矩阵RCPA具体可表示为
(4)
式中,O1=πMsinθk;Ω1=π(2MN-M-N)sinθk;Ψ1=π(2MN-M-N)sinθk;R(du)=R(xi-xj)表示波程差,每个波程差du所对应的元素个数为w(du)。
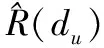
(5)
式中,Ri(du)表示波程差du所对应的所有元素中的第i个元素。
由差联合阵列的定义可知,互质阵列的连续差联合阵列为
{-MNd,-(MN-1)d,…,-d,0,
d,…,(MN-1)d,MNd}
(6)
因此,可利用存在的波程差信息构造与连续差联合阵列相对应的均匀线阵输出向量Z表示为
(7)
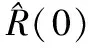
(8)
Z=ΦS+w
(9)
式中,w表示(2MN+1)×1维稀疏向量,其除了第(MN+1)元素外其余元素均为0;Φ为(2MN+1)×K维虚拟阵列流型矩阵,其导向矢量为
(10)
通过上述的预处理操作,阵列自由度得到了增加。利用2M+N-1个阵元能得到MN个阵列自由度,因此最多可同时对MN个信号进行DOA估计。
2.2 基于全变分范数最小化的DOA估计方法
对于式(9),可将其看作单快拍DOA估计问题,目前主流的方法是基于稀疏重构的思想进行求解。然而传统稀疏重构方法都是直接采用在l2空间的范数来度量稀疏参数,需要进行离散化处理来构造完备字典,这就不可避免会存在模型不匹配问题。要从根本上解决模型不匹配问题,最好的方法是采用连续建模法,即在对稀疏域建模时直接采用连续处理的方法而不对稀疏域进行离散化。本文引入全变分范数[26-27]用于DOA估计, 将范数定义在连续空间内从根本上解决模型不匹配问题,提高了估计精度和分辨性能。
首先给出全变分范数‖‖TV的定义,对于一个复测量数据s, 其全变分范数‖s‖TV可定义为
(11)
式中,sup表示取上确界;Bj表示集合[0,1]中不交连可测量的子集。
进一步对式(9)两边同乘以e-j2πnd/λ,同时令τk=d(1-sin(θk))/λ∈[0,1],可得
e-j2πnd/λw(n)=
(12)
式中,n=-MN,-MN+1,…,MN-1,MN。式(12)的矩阵形式可表示为
r=Fs+n
(13)
式中,Fm,n=e-j2πm τn;n为一个稀疏的噪声向量;r=[r(-MN),…,r(MN)]T;s=s(τ),0≤τ≤1,s(τ)在连续域上可表示为
(14)

为了实现对s(τ)的精确估计,构建一个代价函数,分别利用全变分范数和L1范数惩罚项对角度和噪声项进行约束,即
(15)
式中,η是权衡TV范数和L1范数项的正则化参数。
对于式(15)的优化问题,其原始变量是无穷维的,直接求解是十分困难的。这里,考虑利用其对偶性将其转化为易解的半正定规划问题,最后通过其对偶解得到原始变量的解。其对应的对偶形式为
s.t. ‖FHc‖∞≤1, ‖c‖∞≤η
(16)
式中,对偶变量c是有限维的,但约束条件是无限维的仍不能直接求解。幸运的是第一个约束条件可利用有限维线性矩阵不等式进行替代。因此,进一步可转换成半正定规划问题进行求解,即
(17)

通过上述的求解过程可知,本文方法通过利用全变分范数巧妙解决了传统稀疏重构DOA估计算法中模型不匹配和约束等容条件之间的矛盾问题,无需在两者之间采取折衷的办法,从而提高了估计精度。
3 仿真实验与分析
本节中将通过仿真实验对本文方法的估计性能进行验证,并与文献[14]的SS-MUSIC方法以及文献[22]的L1-CSPR方法进行比较。选用互质阵列作为接收阵列,阵元数为10,其中,M=3,N=5。背景噪声为非均匀噪声,信噪比(signal-to-noise ratio, SNR)定义为
(18)
实验中以均方根误差(root mean square error, RMSE)作为算法性能评价标准,DOA估计的RMSE定义为
(19)

3.1 可行性分析
为验证本文方法对欠定条件下DOA估计的有效性,假设15个等功率信号入射到互质阵列上,波达方向分别为[-62.57°,-49.68°,-39.24°,-30.63°,-22.45°,-14.79°,-7.61°,-0.26°,6.93°,13.97°, -21.67°,29.81°,38.37°,48.19°,60.51°],实验中所使用的快拍数L=500,信噪比SNR=10 dB,3种方法的估计结果如图2所示。
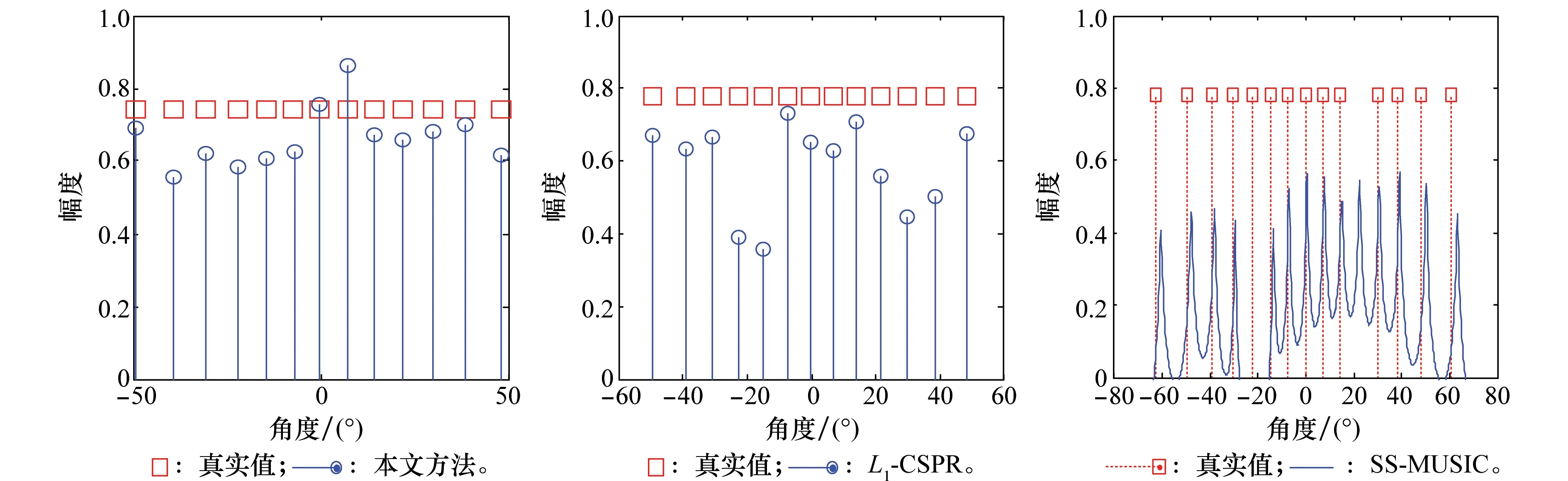
图2 3种方法的估计结果比较Fig.2 Comparison of the results of three methods
由图2的实验结果可知,在不超过阵列自由度的条件下,本文方法与L1-CSPR方法依然具有良好的估计效果,而SS-MUSIC方法的估计效果不佳,甚至会出现个别信号DOA估计错误的情况,这是因为非均匀噪声的存在影响了信号子空间与噪声子空间的正确分离,从而导致估计效果不佳。
3.2 估计精度分析
本实验条件与实验1相同,分析信噪比、快拍数对3种方法估计精度的影响。对于L1-CSPR方法,Δ为完备字典的间隔,分别取1°、0.5°、0.2°,对于SS-MUSIC方法,其角度搜索间隔为0.1。每个SNR、快拍数下进行500次蒙特卡罗实验。图3为快拍数为L=500,信噪比变化范围为-8~8 dB时,步长为2时, 3种方法的RMSE随SNR变化曲线;图4为SNR=0 dB,快拍数变化范围为100~600时,步长为100时,3种方法的均方根误差随快拍数变化曲线。

图3 RMSE随SNR变化曲线Fig.3 RMSE versus different SNR
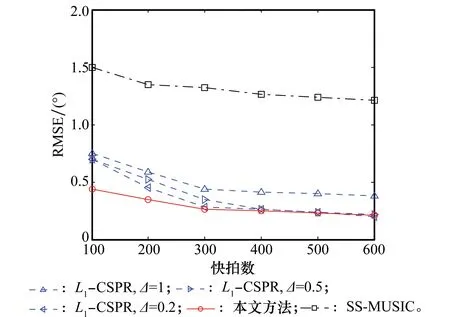
图4 RMSE随快拍数变化曲线Fig.4 RMSE versus different snapshot number
由图3和图4的实验结果可知,L1-CSPR方法的估计精度与完备字典的间隔有着直接的关系,当完备字典的间隔较大时,入射信号的DOA与完备字典之间不匹配,导致估计性能明显下降,随着完备字典间隔的减少,估计精度随之增加。而本文方法在整个角度域对DOA进行估计,无需构造完备字典,有效避免了模型不匹配对估计精度的影响。在相同的实验条件下,本文方法的估计精度要高于L1-CSPR和SS-MUSIC方法,尤其在低信噪比、少快拍数情况下更明显。
3.3 分辨概率分析
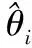
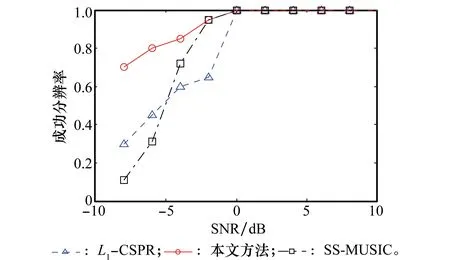
图5 成功分辨概率随SNR变化曲线Fig.5 Successful resolution probability versus SNR
由图5的实验结果可知,在一定的SNR范围内,3种方法成功分辨概率均随着SNR的增加而增大。当SNR>0 dB时,3种方法的分辨成功概率都达到100%。在低SNR条件下,本文方法的成功分辨概率要高于L1-CSPR方法和SS-MUSIC方法。
3.4 运算时间比较
本实验条件与实验1相同,将本文方法与L1-CSPR方法、SS-MUSIC方法的运算时间进行比较。L1-CSPR方法的完备字典间隔为0.1°,SS-MUSIC方法的角度搜索间隔为0.1°。仿真环境:Matlab 8.1平台,英特尔 i7处理器,8 GB内存。具体实验结果如图6所示。
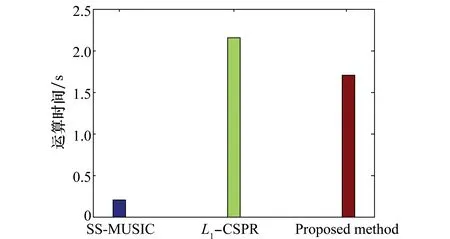
图6 运算时间比较Fig.6 Comparison of calculation time
由图6的实验结果可知,本文方法的运算时间处于L1-CSPR方法与SS-MUSIC方法之间,然而考虑到其在估计精度以及分辨力等方面的良好性能,这种运算性能的损失是可以接受的。
4 结 论
本文以互质阵列为基础研究了基于全变分范数最小化的DOA方法,用于解决非均匀噪声背景下的欠定DOA估计问题。理论分析与仿真实验表明,该方法具有良好的阵列扩展特性,利用2M+N-1个阵元最多可同时对MN个信号进行DOA估计。相对于现有方法,该方法无需进行预白化处理,同时在连续角度域对DOA进行估计,有效避免了传统稀疏重构算法中由于角度域离散化所导致的模型失配问题对估计性能的影响,提高了估计精度和分辨性能。
[1] SCHMIDT R O. Multiple emitter location and signal parameters estimation[J]. IEEE Trans.on Antennas and Propagation, 1986, 34(3):267-280.
[2] ROY R, KAILATH T. RSPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Trans.on Antennas and Propagation, 1989, 37(3):984-995.
[3] PESAVENTO M, GERSHMAN A M. Maximum likelihood direction of arrival estimation in the presence of unknown nonuniform noise[J]. IEEE Trans.on Signal Processing, 2001, 49(7):1310-1324.
[4] QI C Y, CHEN Z J, WANG Y L, et al. DOA estimation for coherent sources in unknown nonuniform noise fields[J]. IEEE Trans.on Aerospace and Electronic Systems, 2007, 43(3):1195-1204.
[5] CHIAO E C, LORENZELLI F, KUNG Y. Stochastic maximum likelihood DOA estimation in the presence of unknown nonuniform noise[J].IEEE Trans.on Signal Processing, 2008, 56(7):3038-3044.
[6] 刘国红,孙晓颖,王波.非均匀噪声下频率及二维到达角的联合估计[J].电子学报,2011, 39(10): 2427-2430.
LIU G H, SUN X Y, WANG B. Joint estimation for frequency and 2-D DOA in nonuniform noise[J]. Acta Electronica Sinica, 2011, 39(10):2427-2430.
[7] 潘婕,周建江,汪飞.非均匀噪声稀疏均匀圆阵的二维DOA估计[J].航空学报,2011, 32(3): 448-456.
PAN J, ZHOU J J, WANG F. 2-D DOA estimation for sparse uniform circular array in presence of unknown noise[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(3):448-456.
[8] SEGHOUANE A K. A Kullback-Leibler methodology for unconditional ML DOA estimation in unknown nonuniform noise[J]. IEEE Trans.on Aerospace and Electronic Systems, 2011, 47(4): 3012-3021.
[9] GONCHAROVA A A, WEBER R J, HUANG Y. Sparse array DOA estimation in the presence of unknown non-uniform noise[C]∥Proc.of the IEEE Aerospace Conference, 2011:1-8.
[10] YANG P, LIU Z, JIANG W L. Improved sparse Bayesian learning method for direction-of-arrival estimation in non-uniform noise[J]. Journal of Electromagnetic Waves and Applications, 2014, 28(5): 563-573.
[11] LIAO B, HUANG L, CHAN S C. New approaches to direction of arrival estimation with sensor arrays in unknown nonuniform noise[J].IEEE Sensor Journal,2016,16(24):8982-8989.
[12] JUN W, BIN L, CHONG T G. Spatial smoothing based methods for direction of arrival estimation of coherent signals in nonuniform noise[J]. Digital Signal Processing, 2017, 67: 116-122.
[13] TIAN Y, SUN X. DOA estimation in the presence of unknown nonuniform noise without knowing the number of sources[J]. International Journal of Electronics Letters,2016,4(1):108-116.
[14] PAL P, VAIDYANATHAN P P. Nested arrays: a novel approach to array processing with enhanced degrees of freedom[J]. IEEE Trans.on Signal Processing, 2010, 58(8): 4167-4181.
[15] VAIDYANATHAN P P, PAL P. Sparse sensing with co-prime samplers and array[J]. IEEE Trans.on Signal Processing, 2011, 59(2):573-586.
[16] LIU C L, VAIDYANATHAN P P. Remarks on the spatial smoothing step in coarray MUSIC[J]. IEEE Signal Processing Letters, 2015, 22(9): 1438-1442.
[17] WENG Z, DJURIC P M. A search-free DOA estimation algorithm for coprime arrays[J]. Digital Signal Processing, 2014, 24(1): 27-33.
[18] ZHANG Y D, QIN S. AMIN M G. DOA estimation exploiting coprime arrays with sparse sensor spacing[C]∥Proc.of the IEEE International Conference on Acoustics, Speech and Signal Processing, 2014: 2267-2271.
[19] QIN S, ZHANG Y D, AMIN M G. Generalized coprime array configurations for direction-of-arrival estimation[J]. IEEE Trans.on Signal Processing, 2015, 63(6): 1377-1390.
[20] HE Z Q, SHI Z P, HUANG L, et al. Underdetermined DOA estimation for wideband signals using robust sparse covariance fitting[J]. IEEE Signal Processing Letters, 2015, 22(4): 435-439.
[21] TAN Z, NEHORAI A. Sparse direction of arrival estimation using co-prime arrays with off-grid targets[J]. IEEE Signal Processing Letters, 2014, 21(1): 26-29.
[22] HE Z Q, SHI Z P, HUANG L. Covariance sparsity-aware DOA estimation for nonuniform noise[J]. Digital Signal Processing, 2014, 28: 75-81.
[23] PAL P, VAIDYANTHAN P P. Pushing the limits of sparse support recovery using correlation information[J]. IEEE Trans.on Signal Processing, 2015, 63(3): 711-726.
[24] CHI Y, SCHARF L L, PEZESHKI A. Sensitivity to basis mismatch in compressed sensing[J]. IEEE Trans.on Signal Processing, 2011, 59(5): 2182-2195.
[25] HOCTOR R T, KASSAM S A. The unifying role of the coarray in aperture synthesis for coherent and incoherent and imaging[J]. Proceedings of the IEEE, 1990, 12(10):735-752.
[28] GRANT M, BOYD S. CVX: Matlab software for disciplined convex programming, version 2.0 beta.[EB/OL].[2016-11-03]. http:∥cvxr.com/cvx.
