基于重复控制的遥感器两轴随动同步控制系统
2018-03-14郝中洋何海燕于飞李超李婧
郝中洋 何海燕 于飞 李超 李婧
基于重复控制的遥感器两轴随动同步控制系统
郝中洋1,2何海燕1于飞1李超1李婧1
(1 北京空间机电研究所,北京 100094)(2 先进光学遥感技术北京市重点实验室,北京 100094)
扫描系统可以使光学遥感器获得更大的成像幅宽。为实现大角度扫描,光学系统采取扫描主镜和半角随动镜的两轴形式。文章对光学遥感器扫描系统两轴随动的同步控制问题进行了研究,针对两轴随动装置周期性较强的特点,提出在主从同步系统的常规PID控制系统基础上增加重复控制环节,重新设计了一个改进的同步控制器。利用重复控制对周期性外激励信号的跟踪、抑制性好的特点,增强系统对同步误差的抑制作用。仿真结果表明,利用重复控制理论设计的同步控制器在保证原有系统跟踪精度和动态性能的前提下,有效的减小了扫描成像时间段内的同步角度误差。扫描成像阶段内同步误差减小了78%。
同步控制 重复控制 两轴随动 光学遥感器
0 引言
扫描系统可以使光学遥感器获得更大的成像幅宽。但由于扫描系统旋转的范围相对较小,导致入射角与镜面间的夹角较大,使得光线发生偏振,难以实现大角度扫描。针对此问题,光路设计中除原有的主转动装置外,需再加入一个次级转动反射镜,跟随主转动装置的运动,使系统获得无像旋、偏振小、大幅宽的优势,但需要解决主、次转动系统的同步性问题[1]。
同步控制在机床加工、机械传动和光刻机等多个领域已经有较为深入的研究,目前比较流行的方法有非耦合式同步控制和耦合式同步控制[2]。非耦合控制对于同步误差而言,是一种开环控制,同步误差较大,此种方法多用于同步位置精度要求较低的传动电机的同步等领域。若同步系统中的子系统的被控对象模型差异较大,或扰动较大时,采用非耦合式同步控制会造成较大的同步误差[3]。对于同步误差要求较高的系统,需要把同步误差作为反馈量形成闭环,反馈到子系统的控制器中。同步误差会影响子系统的控制,即几个需要同步的子系统间控制相互耦合,控制算法也相对复杂。就反馈的方式而言,同步误差反馈到部分子系统中称之为主从同步控制,同步误差反馈到全部子系统中称之为协调同步控制[4]。文献[5-6]提出了基于广义预测控制[7]的两轴同步控制算法,包含了两轴之间的交叉耦合作用,克服了单个电动机受到扰动时两轴不能精确同步的问题。
重复控制是一种学习控制方法,用于高精度跟踪一个周期已知的参考输入。因为它控制精度高、易于实现和控制性能的非参数依赖性等优点,是一种解决周期性外激励信号控制问题的有效方法[8-9]。
本文对光学遥感器扫描系统两轴随动的同步控制问题进行了研究,针对两轴随动装置周期性较强的特点,采用重复控制方法,结合主从控制,提出了一种用于实现扫描主镜—半角随动镜的两轴同步控制系统,取得了良好的控制效果。
1 问题的描述
1.1 扫描装置简述
本文采用的扫描方式为连续360°的旋转扫描模式[10]。主要装置为扫描主镜和半角随动镜,如图1所示。扫描主镜采用从–180°到180°做单向连续变速扫描运动,频率为0.5Hz,半角反射镜为双面反射镜,从–180°到180°做单向连续变速扫描运动,以0.5倍速度对扫描主镜的转动角度进行扫描。扫描主镜、半角随动镜均采用同步力矩电机驱动,两轴在机械上相互独立。
由于上述装置的工作模式为360°连续旋转扫描,每圈的运动特点相同。控制系统的输入呈现周期性,并且电机转轴的轴系摩擦、力矩电机磁场分布等干扰与转动周期相同,即频率为0.5Hz。故上述装置的运动误差、同步误差都呈现周期性。
1.2 电机模型建立


式中 t为时间;R为电机线圈电阻;Ld和Lq分别为直轴、交轴线圈电感;记线圈电感;为交轴线圈电流;为由转自永磁体产生的定子绕组的磁链;为电机极对数;为转子机械角速度;为电机转矩;为电机的电流力矩系数;为电机的反电势系数。对于面装式永磁同步电机,,。简化后的模型与直流电机数学模型类似,如图2所示。

1.3 同步控制系统的建立
对于单轴而言,其控制系统回路为图3所示。

图3 单电机转轴的控制系统框图
本文研究的光学遥感扫描系统若采用非耦合式同步控制,则当其中一轴受到扰动时,其它轴不会对其作出响应,非扰动轴的控制特性不会受到干扰,但对于光学系统而言,其光轴已经改变,故本文的两轴随动系统需设计耦合式同步控制系统,其框图如图4所示。
定义的同步误差为
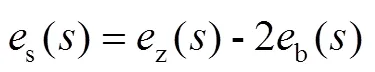
2 同步控制器的设计
2.1 基于重复控制的同步控制器设计
两轴随动系统采用连续360°的旋转扫描模式。针对两轴随动装置运动的周期性较强的特点,同步控制器模型为比例、积分、微分(proportion,integral and differential,PID)控制器加重复控制器[13]的方式。同步控制器的结构如图5所示。
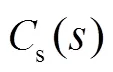

为了更直观的说明同步控制器rc()中1()和()的形式,本文借助离散系统复平面的方式说明。
图5中,虚线框内系统rc(),离散化后的闭环系统框图表示为图6。
图6中系统误差与输入信号间的传递函数为
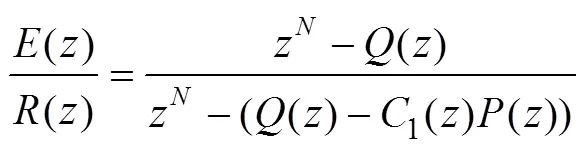
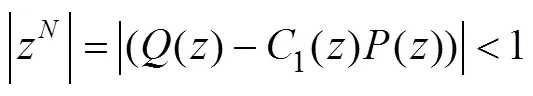

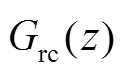
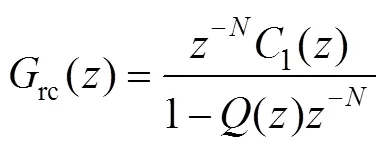
2.2 同步控制器稳定性分析
根据上述分析,为改进同步控制系统的特性,可以将重复控制器并联至同步控制器的PID调节器上。由于系统带有非线性环节,为了分析系统的稳定性,本文采用连续系统重构谱[7]的概念进行稳定性分析。
图4中所示系统中,扫描主镜系统回路传递函数为

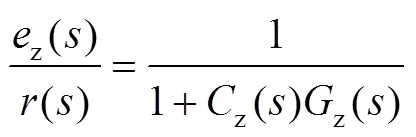
此回路不受同步误差影响,与单轴设计方法没有区别。控制器设计方法可采用PID设计或频域校正法,此部分不做赘述。
半角随动镜回路中,半角随动镜的驱动电压()为半角随动镜控制器输出电压b()与同步控制器输出电压s()的和。即

推导得系统输入到同步误差的传递函数为

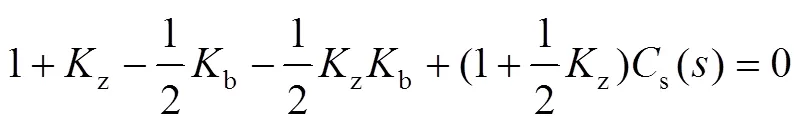


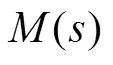
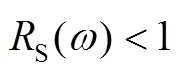
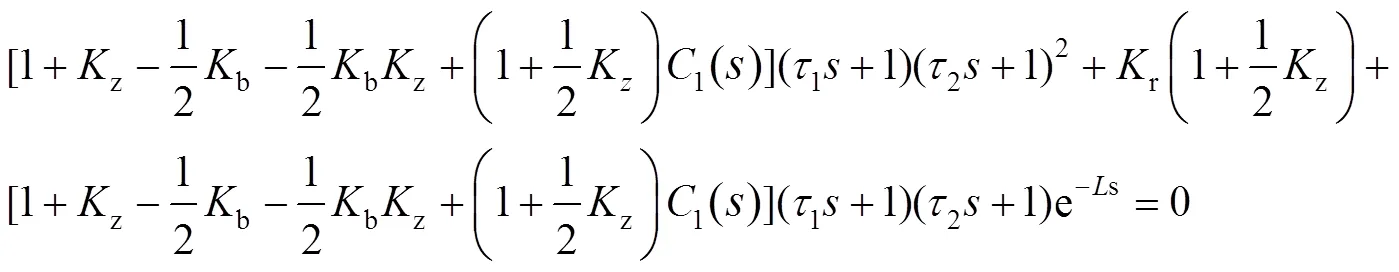
式中1和2分别为器()和2()的时间常数。
同步控制系统的稳定性条件为:

3 仿真分析
为了验证本文提出的控制策略的有效性,本文采用仿真软件MATLAB/Simulink对系统进行了仿真。主镜和半角随动镜的扫描方式为连续360°的旋转扫描模式。扫描角加速度、角速度、角度曲线如图7所示。
根据公式(2),扫描主镜回路电机模型为

半角随动镜回路的电机模型为

重复控制器加入前,同步控制系统中的主镜误差曲线见图8,随动误差曲线见图9,无重复控制器时的同步误差曲线见图10。
根据上文控制器设计,重复控制器加入后系统仍然可以保持稳定。加入重复控制器的同步控制系统仿真结果见图11。
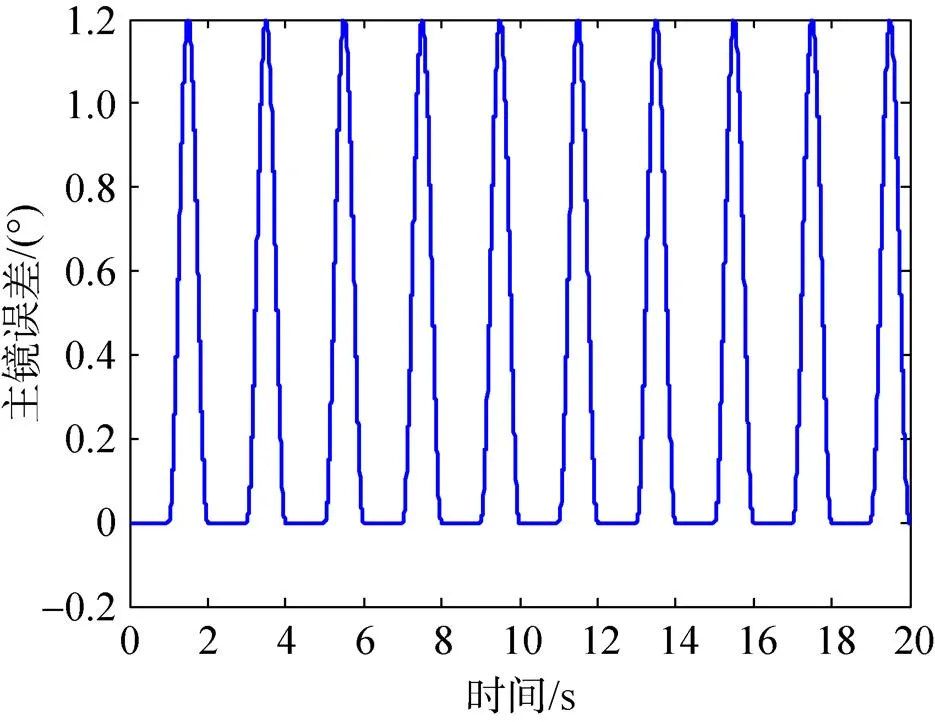
图8 主镜误差曲线

图9 随动误差曲线
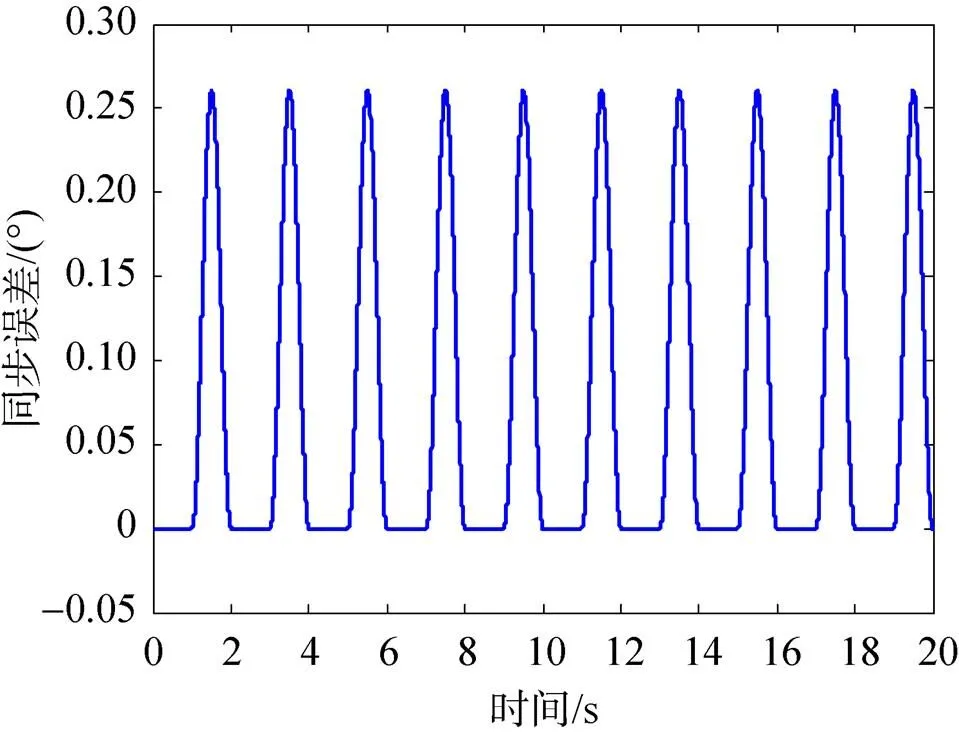
图10 无重复控制器时的同步误差曲线
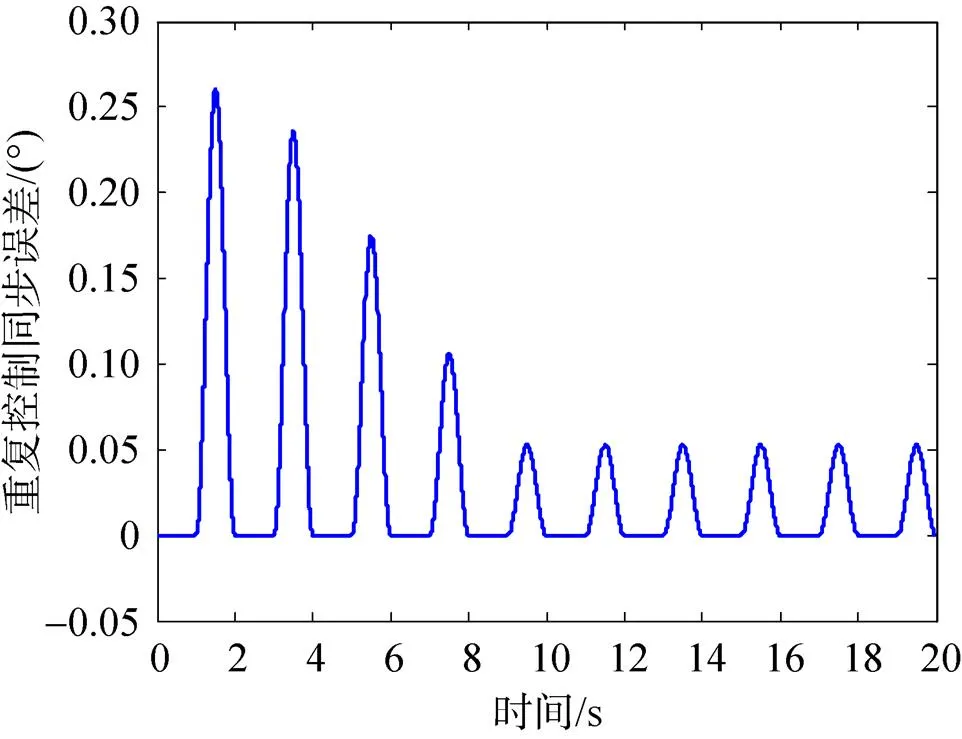
图11 加入重复控制器时的同步误差曲线
由于重复控制是一种学习算法,故1个周期无法表现出它的优势。由图11所示,系统的同步误差从第1个周期后开始衰减。随着输入周期的推移,重复控制器的优点逐步体现出来。第5个扫描周期时,同步误差的峰值由0.264°减小至0.058°,减小了78%。
4 结束语
为解决某遥感器两轴随动系统扫描成像过程中扫描主镜和半角随动镜的运动同步性问题,利用重复控制对周期性外激励信号的跟踪、抑制性好的特点,提出在主从同步系统的常规PID控制系统基础上增加了重复控制环节,给出了系统的输入至同步误差的传递函数。依据重构谱的概念给出了同步系统重复控制器稳定性条件。依据稳定性条件,设计了重复控制器的参数。仿真结果表明,改进的同步控制系统稳定,保证了系统同步的精度,扫描成像阶段内同步误差减小了78%,达到了重复控制器的设计目的,提高了两轴随动系统的同步性能。
[1] 迟东南, 李晓曼. 基于广义预测的双转动扫描系统同步控制[J]. 航天返回与遥感, 2014, 35(5): 61-71. CHI Dongnan, LI Xiaoman. Synchronization Control for Dual-revolution Scanning System Based on Generalized Predictive Algorithm[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(5): 61-71. (in Chinese)
[2] SHAN Jinjun, LIU H H T. Synchronized Tracking Control of Multiple Flying Wings[C]. American Control Conference, Minneapolis, USA, 2006.
[3] WOLFE R E, LIN G, NISHIHAMA M. NPP VIIRS Early On-orbit Geometric Performance[C]. SPIE Optical and Photonics Conference, San Diego, USA, 2012.
[4] XIAO Y, ZHU K Y. Optimal Synchronization Control of High-precision Motion Systems[J]. IEEE Transactions on Industrial Electronics, 2006, 53(4): 1160-1169.
[5] 刘笃喜, 程益恒, 赵小军, 等. 双电机驱动卷绕式系统转速同步控制研究[J]. 机械制造, 2012, 50(8): 32-35. LIU Duxi, CHENG Yiheng, ZHAO Xiaojun, et al. Dual-motors-driven Spiral Wound System Rotate Speed Synchronization Control[J]. Machinery, 2012, 50(8): 32-35. (in Chinese)
[6] KOREN Y. Cross-coupled Biaxial Computer Control for Manufacturing Systems[J]. Journal of Dynamic Systems Measurement and Control, 1980, 102(4): 265-272.
[7] 盛华, 方强. 基于广义预测的双电机同步控制[J]. 机电工程, 2010, 27(3): 107-110. SHENG Hua, FANG Qiang. Biaxial Synchronization Based on Generalized Predictive Control[J]. Journal of Mechanical and Electrical Engineering, 2010, 27(3): 107-110. (in Chinese)
[8] 李翠艳, 张东纯, 庄显义. 重复控制综述[J]. 电机与控制学报, 2005, 9(1): 37-44. LI Cuiyan, ZHANG Dongchun, ZHUANG Xianyi. Repetitive Control - a Survey[J]. Electric Machines and Control, 2005, 9(1): 37-44. (in Chinese)
[9] 杨松, 曾鸣, 苏宝库. 重复控制算法在转台伺服系统中的应用[J]. 电机与控制学报, 2007, 11(5): 508-511. YANG Song, ZENG Ming, SU Baoku. Repetitive Control Algorithm in Turntable Servo System[J]. Electric Machines and Control, 2007, 11(5): 508-511. (in Chinese)
[10] 王恺, 刘兆军. 摆动扫描的迭代学习控制系统研究[J]. 航天返回与遥感, 2008, 29(1): 34-38. WANG Kai, LIU Zhaojun. Iterative Learning Control System of Scan for Oscillating Mirror[J]. Spacecraft Recovery & Remote Sensing, 2008, 29(1): 34-38. (in Chinese)
[11] 李培芳, 孙士乾. 三相电路瞬时电流、功率的分解与Park空间分析[J]. 浙江大学学报(工学版), 2001, 35(1): 14-16. LI Peifang, SUN Shiqian. Decomposition of Instantaneous Current and Instantaneous Power of Three-phase Circuits and Park Space-domain Analysis[J]. Journal of Zhejiang University (Engineering Science), 2001, 35(1): 14-16. (in Chinese)
[12] 陈嫦娥, 毛承雄, 王丹, 等. 多相交流系统的Park变换[J]. 高电压技术, 2008, 34(11): 2475-2482. CHEN Change, MAO Chengxiong, WANG Dan, et al. Park Transformation of Multiphase AC Systems[J]. High Voltage Engineering, 2008, 34(11): 2475-2482. (in Chinese)
[13] 马亚丽, 靳宝全, 程珩. 重复控制补偿的PID电液伺服位置控制[J]. 流体传动与控制, 2010(2): 31-33. MA Yali, JIN Baoquan, CHENG Heng. PID Electro-hydraulic Servo Positon Control with Repetitive Control Compensation[J]. Fluid Power Transmission and Control, 2010(2): 31-33. (in Chinese)
[14] LANDAU I D, CONSTANTINESCU A, REY D. Adaptive Narrow Band Disturbance Rejection Applied to an Active Suspension - an Internal Model Principle Approach[J]. Automatica, 2005. 41(4): 563-574.
[15] TAN W, MARQUEZ H J, CHEN T. IMC Design for Unstable Processes with Time Delays[J]. Journal of Process Control, 2003, 13(3): 203-213.
[16] 张东纯. 重复控制及其应用研究[D]. 哈尔滨: 哈尔滨工业大学, 2004. ZHANG Dongchun. Reserch and Application on Repetitive Control[D]. Harbin: Harbin Institute of Technology, 2004.
[17] 张倩. 基于重复控制的永磁同步电机伺服系统研究[D]. 哈尔滨: 哈尔滨工业大学, 2014. ZHANG Qian. Sturyon the Servo System of PMSM Based on Repetitive Control[D]. Harbin: Harbin Institute of Technology, 2014. (in Chinese)
[18] SRINIVASAN K, SHAW F R. Analysis and Design of Repetitive Control Systems using the Regeneration Spectrum[C]. American Control Conference, San Diego, USA, 1990.
[19] 胡寿松. 自动控制原理[M]. 北京: 科学出版社, 2001. HU Shousong. Principle of Automatic Control[M]. Beijing: Science Press, 2001. (in Chinese)
(编辑:庞冰)
Two-axis Servo Synchronous Control System for Optical Remote Sensor Based on Repetitive Control
HAO Zhongyang1,2HE Haiyan1YU Fei1LI Chao1LI Jing1
(1 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China)(2 Beijing Key Laboratory of Advanced Optical Remote Sensing Technology, Beijing 100094, China)
Scanning system can make the optical remote sensor have a larger imaging width. In order to scan in a wide-angle range, the two-axis scanning pattern, including a master scanning mirror and a slave half-angle follower, is often selected in the optical design. In this paper, two-axis servo synchronous control was studied for optical remote sensor scanning system. Taking advantage of the strong periodicity characteristic in two-axis servo device, the conventional PID control scheme was updated by adding a repetitive control link in the master-slave synchronization system, and at the same time an improved synchronous controller was also redesigned. As the repetitive control has better track /suppress characteristic to periodic external pumping signal, the system synchronous error was greatly inhibited. From the simulation results, one can find that the design of the synchronous controller based on control theory, is effective to decrease the synchronous angular error during the scan imaging phase, in addition to maintaining the required tracking accuracy and dynamic performance. The synchronization error was reduced by 78% during the scan imaging phase.
synchronous control; repetitive control; two-axis servo; optical remote sensor
TP293
A
1009-8518(2018)01-0069-09
10.3969/j.issn.1009-8518.2018.01.009
郝中洋,男,1986年生,2012年获哈尔滨工业大学控制科学与工程系硕士学位,工程师。研究方向为电机驱动与控制。E-mail: hithzhy@gmail.com。
2017-07-27
国家重大科技专项工程
