配电网节能降损优化研究综述

2018-03-13贾勇晨葛丽娟

山西电力 2018年1期

贾勇晨，葛丽娟

（内蒙古农业大学,内蒙古呼和浩特 010000）

0 引言

配电网处于电力系统的末端,是为用户输送与分配电能的重要组成部分,对配电网节能降损技术的研究具有重要的现实意义。

对配电网的结构与负荷进行分析,寻找最优的运行方式,为配电网的优化运行提供理论基础。配电网运行方式的优化,就是改变配电网络中各支路分段开关与支路之间的联络开关的状态,对配电网的结构进行重构。近年来,对于配电网优化规划的算法与模型的研究都有了很大的发展,有了多种方式的配电网规划方法。

1 配电网节能降损的数学模型

1.1 目标函数

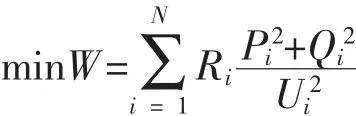
上式中W为线路损耗,i为支路编号,Pi为对应支路的有功功率,Qi为对应支路的无功功率,Ri为对应支路的的电阻值,Ui为对应支路前段节点电压。

1.2 约束条件

对配电网进行重构时,不仅需要满足潮流方程的约束,还需要满足线路容量、电压、电流的约束和网络结构辐射状运行约束。

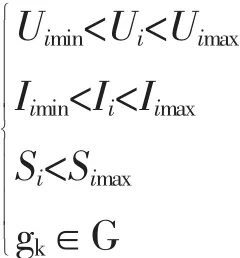
式中，Ui、Uimin、Uimax分别为节点的电压、电压下限、电压上限；Ii、Iimin、Iimax分别为节点的电流、电流下限、电流上限；Si与Simax为流过线路的功率与容许最大值；gk为迭代之后的网络结构。G为配电网规划后得到的辐射状网络结构集合[1]。

2 配电网运行方式优化

配电网络通常呈放射状运行，因此其重构问题实际上是在弧的权值随流量非线性变化的网络上寻找最小费用树的问题，这一大规模、混和整型、非线性组合优化问题，属于非确定性多项式问题[2]。现阶段求解这类问题主要采用的方法：利用数学理论的算法、根据启发式的算法、人工智能算法。新兴的电力电子器件改变了配电网的运行方式,同样达到了对配电网节能降损的作用。

2.1 数学方法求解配电网重构

对配电网进行重构时,使用数学方法求解,就是根据现有的数学理论对配电网进行重构。文献[3]在求解配电网重构模型时,提出利用动态规划算法,将重构问题分解成需要进行多阶段决策的问题。文献 [4]利用0-1整数规划的方法将网损最小作为目标函数,对网络进行规划。文献 [5]将求解重构问题转化为求解一个非线性整数优化问题。文献 [6]利用分时段优化对动态重构中重构区间进行划分,构造含开关操作费用及阶梯式电价的综合目标函数；文献 [7]将锥优化的思想融入到配电网重构当中,通过目标函数线性化和约束条件的锥转化,对基本模型进行等价变换,生成配电网锥优化模型；文献 [8]提出了一种配电网差异化节能规划思路,建立了基于前推回代潮流计算法和灰色关联度预测法的节能潜力模型。

运用数学方法的优势是可以在有限的时间内求解出局部的最优解,现如今随着配电网逐渐增大,利用数学方法计算重构问题,计算时间有时会长到无法满足工程的要求,故数学方法求解配电网重构问题只适用于小规模的配电系统当中,无法满足当前大规模的配电网络。

2.2 启发式算法求解配电网重构

现代启发式算法在求解组合最优问题时表现出了卓越性能,使它在过去20a里受到了人们的广泛关注。启发式算法主要分为支路交换法与最优流算法。文献 [9]针对传统支路交换法每交换一次开关就要进行一回潮流计算的不足,对其进行改进,使算法可以作出符合实际要求的设定,增大了人工可操控度,但改进后的算法只对弱环网结构的配电网有效。文献 [10]提出将最优流模式法改进，对配电网络进行重构,将配电网络重构的问题转换为潮流优化的问题,并且在求解最优流模式时,使用了一种较为快速的单环网潮流算法,其缺点每次闭合开关后都需要进行一次潮流计算,检查电流是否过大；文献 [11]把动态重构问题分解为重构次数与时间间隔的组合,对各时段进行静态网络重构,不需进行潮流分析,缩短了网络重构的时间。

运用启发式算法对配电网进行重构时,需要与配电网重构的特性结合,计算速度较数学方法有了一定的提高,但由于配电网重构自身的特点,系统初始状态会比较容易对结果产生影响,结果不能确定为最优解。

2.3 人工智能算法求解配电网重构

人工智能算法包括：模拟退火法、粒子群算法、禁忌搜索法、蚁群优化算法、混沌优化算法、遗传算法、和声搜索法以及其他人工智能算法。但是单一的人工智能算法常常具有收敛速度较慢,易于陷入局部最优解,鲁棒性不强的特点,现代研究配电网重构问题时通常运用改进的人工智能算法或者将两种算法相结合后再用以求解配电网重构问题。

文献 [12]在对配电网模型进行求解时,引入退火动态罚因子,解决传统遗传算法在收敛速度、爬坡能力、鲁棒性方面的不足,使算法的运行时间缩短,收敛于全局最优解的次数增多。文献 [13]应用回支关联矩阵,使配电网始终为辐射状网络,避免了遗传学算法在进行配电网重构时产生不可行解,再根据最优流算法,生成最优开关断开组合,使寻优效率提升。文献 [14]提出了一种兼顾经济性和电能质量的网络重构方法,再用归一化方法将两者融合,形成配电网性能指标,划分重构时段,缩小了遗传算法的寻优空间,提升了算法的效率。文献 [15]将混沌理论思想加入粒子群算法中,同教学优化算法结合,保证了种群的多样性和防止解的过早收敛,提高了算法的寻优效率。文献 [16]提出了根据Mayeda生成树的新的编码方式,并且提供了相应的解码策略,利用粒子群算法对模型进行求解,根据Mayeda生成树编码的特点,使得解一直处于可行的范围内,提升了算法的效率。文献[17]对配电网进行重构时,为克服人工鱼群算法在收敛速度方面较慢的缺点,将具有局部快速收敛性、易实现性的粒子群算法与其结合,使算法的收敛性、收敛速度得到提升。文献 [18]根据图解蚂蚁系统,对配电网进行重构,这一过程包含两个部分,第一部分完成网络的拓扑结构分析,第二部分通过模拟蚁群在构造图中的行走过程完成搜索寻找最优解。该算法极大地缩小了可行解的范围,使算法的寻优效率得到提高。文献 [19]提出了一种整数型的量子粒子群算法,结合了将量子进化算法与粒子群算法的特点,以负荷曲线的单调性和幅值变化大小为依据,划分时间段,对配电网模型进行重构。文献 [20]分析了配电网结构,将目标配电网用一种基本环矩阵表示；并且提出了一种可以避免不可行解产生的编码方式,再利用改进后的和声搜索算法求解网络重构模型,具有更好的收敛性与寻优快速性。文献 [21-22]分析了配电网动态重构过程中开关的操作次数很难被控制的特点,利用最优模糊C均值聚类法,并将其改进,分别与和声搜索算法、化学反应算法结合,将这一过程分解为多个静态问题,对每一个时间点的网络进行重构,使算法的速度得到很大的提升。文献 [23]提出了一种新型的鸡群优化算法,利用鸡群优化算法的高效全局和局部搜索能力,提高了寻优效率，同粒子群算法进行比较，结果表明鸡群优化算法的寻优速度更快。文献 [24]提出了一种新型的二进制纵横交叉算法,其中横向交叉机制增强了全局搜索能力,纵向交叉机制保持了种群的多样性,避免陷入局部最优解,纵横相结合使算法能够快速寻找到全局最优解。

目前在对配电网进行重构时,利用人工智能算法,可以较快地提升寻找全局最优解的速度,但收敛速度却下降了,同时在求解较为复杂的结构时,通常使得计算量过大,再利用该方法对配电网进行重构时会遇到许多困难。

2.4 新型电力电子器件

智能软开关SNOP (soft normally open point)是安装在联络开关处的新型电力电子装置,是一种能够比较精确地传输相连接的两条线路的有功功率与无功功率的交换。文献 [25]建立了一种使用SNOP后的配电网运行优化模型,详细比较了安装SNOP后的配电网、进行网络重构的配电网,对比结果显示：该方式同时对静态、动态网络潮流都有优化效果,说明了安装SNOP后的配电网具有很高的效率与潜力。

3 配电变压器经济运行

配电网络中的变压器一般装设于线杆或者配电所当中,容量普遍不高,直接向负载供电,是配电系统所有设备中消耗电能最多的,虽然其效率通常很高,但配电网规模较大,变压器的数量就很可观了。因为工作时间长,选择的型号、运行的方式有问题,这样就无法避免地造成了空载损耗。这时就需要让变压器运行在经济运行区间,使损耗最低。

文献 [26]根据变压器的多种运行方式下的损耗曲线,得出了变压器的初始运行区间。通过分析各个运行区间的线路损耗,利用模糊决策法,得到最适合配电变压器的经济运行区间。

负荷的变化会影响变压器的运行,依据负荷的改变对变压器进行配置,使变压器运行在经济区间,通过技术改造来改善变压器经济运行。

4 配电网无功补偿

配电网络线路中包括：有功功率、无功功率。任何配电网络中都存在电阻,也无法避免线路中无功功率的交换,所以当无功电流通过电阻时,网络就会产生电能的损耗。网络中因无功功率的交换,而损耗的电能为

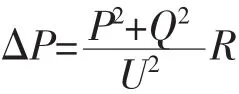
其中，ΔP为电能损耗量,R为电阻,P、Q分别为流经电阻的有功功率与无功功率。

所以配电网电能的损耗,会因为无功功率在网络中的交换而增加,为了降低无功功率流动带来的电能损耗,可以在配电网络中,无功负荷较为集中的区域投入无功补偿,就近提供无功功率。

文献 [27]提出了无功功率的优化模型,通过变压器的有载调压、电容器的就近无功补偿,对配电网络结构进行重构,还将优先次序的原则加入了无功功率优化的过程。

5 结论

配电网节能降损技术仍处于研究阶段,本文从对配电网的运行方式、配电变压器的经济运行、配电网的无功补偿,3个方面综述了配电网节能降损的研究现状及存在的问题,有如下结论。

a）对配电网运行方式的优化是目前配电网节能降损的主要研究方向,具有多种优化方法,研究主要考虑优化算法的收敛性,收敛速度,鲁棒性的强度,各种算法的组合虽然对计算的速度与收敛性都有提高,但是求解的方法仍然需要提高。

b）配电变压器经济运行对降低配电网损耗尤为重要,现阶段对于降低配电变压器损耗的研究应将经济性、运行稳定性、负荷情况综合考虑。

c）目前对配电网进行无功补偿的方法,大都是根据电网无功功率配置的原则,或者是电网设计的规程进行无功功率的补偿,这种方法宏观指导性过强,很难对不同特性的配电网无功功率实现更加优化的配置,应当综合考虑配电网感性与容性的无功,进行无功功率的配置。

虽然当前对配电网节能降损优化的研究比较深入,对配电网运行方式优化的求解方法也有较大的发展,但是在配电网实用性方面依然没有较大的进步,新兴的电力电子器件对于配电网优化方面具有巨大的潜力,但是其技术实现与成本效益仍需进一步研究。

[1] 马草原，孙展展．基于双重混合粒子群算法的配电网重构[J].电工技术学报，2016，31（11）：120-128.

[2] 余贻鑫，段刚.基于最短路算法和遗传算法的配电网络重构[J].中国电机工程学报，2000，20（9）：44-49.

[3] 刘柏私，谢开贵，周家启．配电网重构的动态规划算法 [J]．中国电机工程学报，2005，25(9)：29-34．

[4] A new 0-1 integer programming method of feeder reconfiguration for loss minimization in distribution systems[J].Electric Power Systems Research，1995，33(2)：125-131.

[5] Fan Jiyuan, Zhang Lan, John D M.Distribution network reconfiguration：single loop optimization[J].IEEE Trans on Power Systems，1996，11(3)：1643-1648．

[6] 党存禄，李正发.基于经济性的配电网动态重构优化策略研究 [J].自动化与仪器仪表，2016（4） :112-114.

[7] 于莹莹．基于锥优化的智能配电网优化问题建模方法研究[D].天津：天津大学，2014.

[8] 姜飞，涂春鸣.配电网差异化节能规划方法及其应用 [J].电网技术，2015，39（10）：2712-2718.

[9] 刘秋源，宫诗玖.基于支路交换法的配网重构方法分析 [J].电气开关，2014（5） :55-58.

[10] 邓佑满，张伯明．配电网络重构的改进最优流模式算法 [J]．电网技术，1995，19(7)：47-50．

[11] 董家读，马献乐．基于负荷变化的配电网重构研究 [J]．陕西电力，2013,41 (4):11-14.

[12] 张宁，马孝义．采用退火遗传算法的配电网优化方法 [J]．重庆大学学报，2014，37(2)：76-82．

[13] 黄弦超，杨雨．基于电流分点编码的遗传算法在配电网重构中的应用 [J]．电力系统自动化，2013，37(19)：74-79．

[14] 田昊，吕林．计及电网运行特性的配电网动态重构 [J]．电力系统保护与控制，2015，43(1)：9-15．

[15] 时慧喆，刘志鹏．基于混合优化算法的配电网动态重构研究[J] ．电气技术，2016(6)：41-46．

[16] 林济铿，刘阳升．基于 Mayeda生成树实用算法与粒子群算法的配电网络重构 [J]．中国电机工程学报，2014，34(34)：6151-6158．

[17] 高博，韩冬．基于人工鱼群和粒子群混合算法的配电网重构[J]．东北电力大学学报，2012，32（6）：10-13.