一种耦合支持向量机遗传算法的燃烧优化方法研究

李锦萍，靳智平，王艳玲

（山西大学动力工程系，山西太原 030013）

0 引言

循环流化床技术作为一种新型煤燃烧技术，其燃烧过程的复杂性，运行参数之间呈现出强耦合、非线性、时变、多变量特点，需要对整个变工况燃烧过程进行整体的协调和优化控制。文献[1-4]采用最小二乘支持向量机，改进的遗传算法和神经网络通过对模型参数进行寻优，建立的燃烧特性模型，对单一的目标进行优化时效果比较明显，对于多个强耦合的目标进行优化时呈现出不太理想的效果；文献 [5-7]基于遗传算法对最小二乘支持向量机的参数寻优，实现了热效率和污染物排放的双重优化，而受数据质量问题的制约，不能更加准确地反映模型；文献 [8]运用改进的最小资源神经网络建模方法，处理数据样本，建立NOx排放量和热效率的综合模型，采用改进的遗传算法对已经建立的模型进行了优化，在建模方面虽然能够反映数据和目标的映射规律，提取了数据之间的联系，但对初值的依赖性很大，而且收敛速度比较慢[9]，指导意义不理想。

本文以某300 MW循环流化床锅炉机组为研究对象，模型参数影响因素如图1所示，反映出变工况燃烧过程中各模型参数之间相互影响和制约[10-12]，是一个强耦合、非线性、时变、多变量的控制对象。循环流化床锅炉变工况燃烧优化模型参数输入之间、输出之间、输入与输出之间存在强耦合关系，有必要对整个变工况燃烧过程进行安全性、经济性和污染物排放量的多重优化，才能达到良好的控制效果，优化研究方法如图2所示。

图1 模型参数影响因素分析

图2 优化研究方法

1 模型构建

1.1 数据收集及预处理

根据某300 MW循环流化床机组实际运行情况，在不投油负荷工况下，随机采集了含64种变量参数的45组数据，每一变工况负荷保持30 min以上运行时间，见表1某300 MW循环流化床机组燃烧相关数据（a—实时运行数据）。

采用粗糙集RS理论[13]，根据实时运行数据的特点，计算各模型参数之间的相关度，通过可辨识矩阵，去除无用属性，取出所有仅包核属性的元素，作为约简结果。约简结果包含负荷、主蒸汽温度、主蒸汽压力、主蒸汽流量、汽包水位、给煤量、SO2排放量、烟气量、炉膛差压、排烟温度、氧量、床温、床压、总风量、返料总风量、一次风率、二次风率、NOx排放量、底渣排放量、燃烧效率、钙硫摩尔比和脱硫效率等22种参数，其中将给煤量、总风量、返料总风量作为模型输出，其余作为模型输入。

对约简完的数据进行归一化处理。处理后数据见表1某300 MW循环流化床机组变工况燃烧相关数据（b—归一化数据）。

1.2 建立样本数据

用支持向量回归机建立模型参数影响因素的输入与输出之间关系，将多输入、多输出的非线性样本转变为特征空间的线性样本，从45组数据中随机抽取30组作为模型训练样本，其余15组作为模型验证样本。

2 模型训练

用支持向量回归机编程[14-15]，选择径向基核函数RBF，将归一化数据代入模型进行模型训练。用遗传优化算法[16]优化惩罚函数c和核函数光滑因子g，并将优化结果带入支持向量机程序进行训练，模型训练进化过程如图3所示，终止进化代数为200，最优参数惩罚函数c为4.768 2，核函数光滑因子g为1.413 4，种群数量为20。

表1 某300 MW循环流化床机组变工况燃烧相关数据

图3 模型训练进化过程

3 模型检测、分析与对比

3.1 利用检测样本验证

将15组检测样本数据输入模型，原始数据与回归预测数据比较后误差分布如图4所示，给煤量的绝对误差量为-5×101～5×101t/h，相对误差量为-5×10-1～5×10-1；总风量的绝对误差量为-5×103～5×103Nm3/h，相对误差量为-5×10-3～5×10-3；返料总风量的绝对误差量为-2×102～2×102Nm3/h，相对误差量为-2×10-2～2×102。

3.2 利用训练样本再次检测

将30组训练样本输入模型，原始数据与回归预测数据比较后误差分布如图5训练样本给煤量、总风量、返料总风量误差分布所示，给煤量的绝对误差量为-2×100～2×100t/h，相对误差量为-2×10-2～2×10-2；总风量的绝对误差量为-5×10－3～5×103Nm3/h，相对误差量为-5×10-3～5×10-3；返料总风量的绝对误差量为-2×102～2×102Nm3/h，相对误差量为-1×10-2～1×10-2。

3.3 分析与对比

15组检测样本数据和30组训练样本检测模型的结果显示，给煤量、总风量、返料总风量三者的相对误差量与绝对误差量之比分别为1%和1%、0.000 1%和 0.000 1%、0.01%和 0.005%。相对于原始数据，模型输出的误差非常小，能够实现变工况多重燃烧的优化。

4 结论与建议

全面地分析和研究模型参数之间的影响因素，深度挖掘不同变工况下的实时运行数据，耦合支持向量机和遗传算法构建优化模型，进行的模型训练和验证过程，表明该优化方法减少了对原始数据的依赖性，能够实现多个强耦合目标的优化，达到了预期多重燃烧优化的目的。

在循环流化床锅炉机组投产一段时间后，应综合考虑设备、环境、煤质、操作等不确定性因素，利用已有的历史数据，分析不同负荷工况下的影响因素及其之间的耦合关系，寻找、挖掘工况数据，确定优化目标，进行多目标优化，将优化结果作为依据，减少燃烧优化过程中客观因素和主观因素的影响，实现机组安全、经济和环保运行三赢的目标。

图4 检测样本给煤量、总风量、返料总风量误差分布

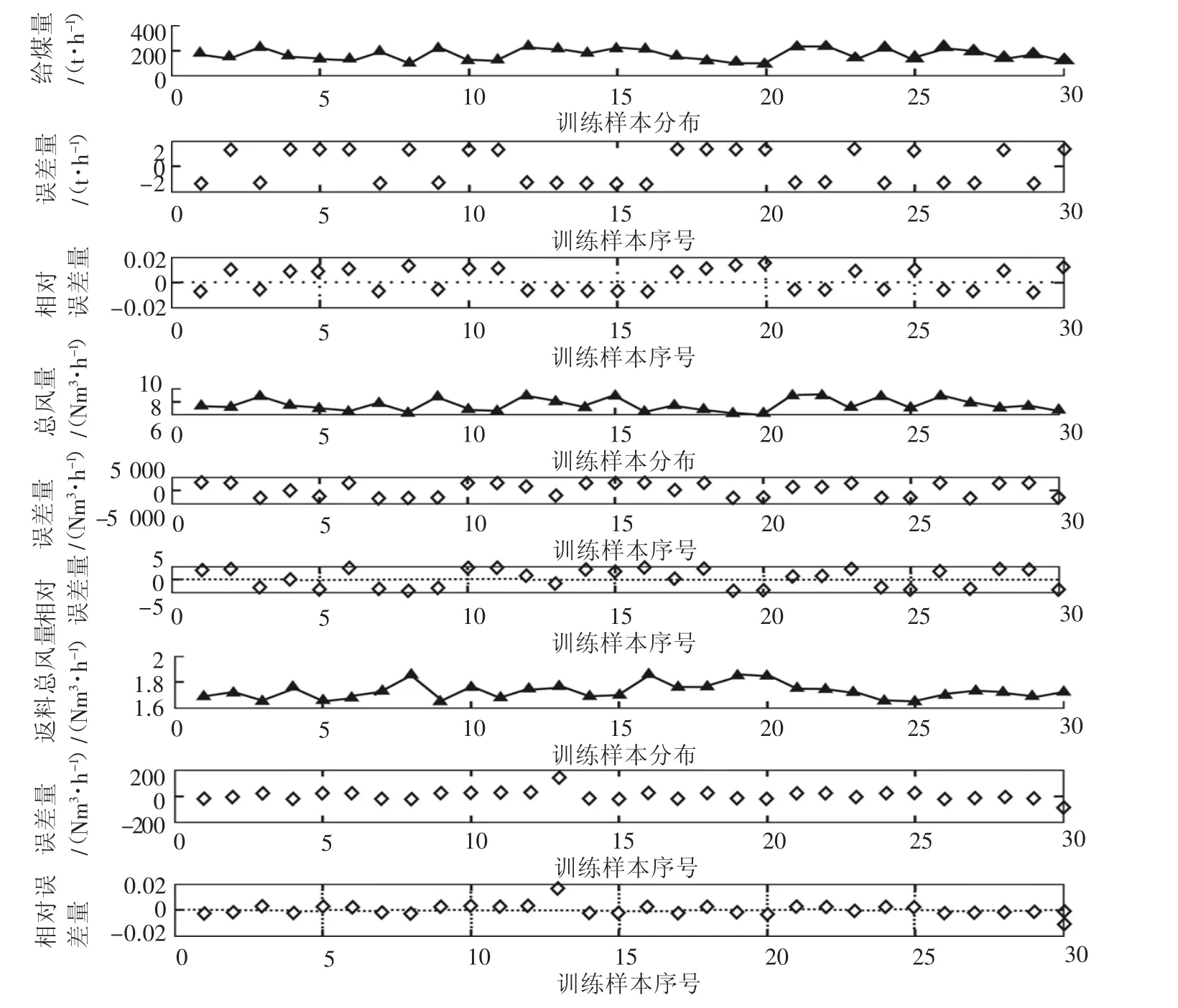
图5 训练样本给煤量、总风量、返料总风量误差分布

[1]周昊,朱洪波.基于人工神经网络的大型电厂锅炉飞灰含碳量建模 [J].中国电机工程学报，2002,22(6):96-100.

[2]王子杰，李健，孙万云.基于神经网络和遗传算法的锅炉燃烧优化方法 [J].华北电力大学学报，2008，35(1):14-17.

[3]顾燕萍，赵文杰，吴占松.采用最优MVs决策模型的电站锅炉燃烧优化 [J].中国电机工程学报，2012，32(2):39-44.

[4]许昌，吕剑虹.基于生成机理的燃煤电站锅炉NOx排放量神经网络模型 [J].中国电机工程学报， 2005,24(10):233-237.

[5]周霞，沈炯，沈剑贤,等.一种新的免疫多目标优化算法及其在锅炉燃烧优化中的应用 [J].东南大学学报:英文版，2010，26(004):563-568.

[6]李建强，刘吉臻，张栾英,等.基于数据挖掘的电站运行优化应用研究 [J].中国电机工程学报，2006，26(20):118-123.

[7]魏辉，陆方，罗永浩,等.燃煤锅炉高效低 NOx运行策略的研究 [J].动力工程，2008,28(3):361-366.

[8]许昌，吕剑虹.电站燃煤锅炉NOx排放神经网络模型 [J].锅炉技术，2005(2):13-17.

[9]焦李成.神经网络系统理论 [M].西安:西安电子科技大学出版社，1990:242-251.

[10]王灵梅，邢德山，蔡新春,等.电厂锅炉 [M].北京：中国电力出版社，2003:298-302.

[11]路春梅，程世庆，王用征.循环流化床锅炉设备与运行 [M].北京：中国电力出版社，2013:62-64.

[12]卢啸风.大型循环流化床锅炉设备与运行 [M].北京：中国电力出版社，2006:203-205.

[13]韩祯祥，张琦，文福拴.粗糙集理论及其应用综述 [J].控制理论与应用，1999，16（2）：16-21.

[14]刘永超.基于人工蜂群算法的循环流化床锅炉燃烧过程优化研究 [D].河北：燕山大学，2014：5-25.

[15]Cristianini N,Shawe-Taylor J，李国正，等 (译).支持向量机导论 [M].北京:电子业出版社，2004.

[16] 刘勇.非数值并行算法 (第二册)遗传算法 [M].北京:科学出版社，2003:1-6.