变角度水面矢量推进器性能分析

吕建刚 张仲志 宋 彬 赵正龙 刘金华

(陆军工程大学车辆与电气工程系， 石家庄 050003)

0 引言

水陆两栖平台能够扩展人类的活动方式，并提高水上与陆地农业生产的转换效率。在现行大方形系数陆面汽车结构的基础上进行改进，能够维持陆上性能、节省结构设计成本。然而，已量产的VW166型、Amphicar Model 770型等大方形系数两栖平台在水中排水航行[1]，受到的兴波阻力与速度的6次方成正比，航速受限难以超过15 km/h[2]；Aquada、Watercar等两栖平台的速度有所提升，但是结构已向船艇发展，方形系数大大减小而偏离了车辆结构[3]。

近年来，普通水面平台不断发展，为大方形系数两栖平台的改进提供了参照。其中，尾部阻流板设计通过增加托举力而减小船体湿面积，进而降低了双体船的阻力[4]；水翼能够增加托举力并抬升船艇前端，进而改变流场获得转矩，实现纵倾，平台阻力下降了20%以上[5-6]；滑行面设计的高速艇滑水航行，由水动力提供托举力和转矩，将艇体托出水面并维持一定的纵倾角，大大提高了航速[7]。因此，增加托举力和转矩驱动，是水面平台减阻提速的有效办法[6-8]。但是将上述研究用于基于汽车结构的两栖平台，则改动较大而严重影响陆上性能，且增加了一套独立的喷水或螺旋桨推进系统，结构复杂化。

南美丛林中的蛇怪蜥蜴踩踏水面，能够获取前进推进力、平衡体重的托举力和维持奔跑姿态的转矩，为推进器设计提供了灵感[9-10]。以蛇怪蜥蜴为仿生对象，徐林森等[11-16]以平板型脚掌、椭圆形轨迹和5 Hz以上高频率踏水模拟设计，获取了推进力、托举力和转矩三维驱动，初步实现了水面平台0.5 m/s的低速运动，正在开展结构稳定性研究；而传统的明轮推进器同样基于平板型叶片结构，以叶片平面径向布置为主，通过叶片圆形轨迹的旋转运动，8～10个叶片、1 r/s左右的低转速设置，提供垂直于轮轴的推进力，但是推进效率还有待提高[17]。结合以上高频灵活、三维驱动输出的平板设计和稳定旋转运动两个特性，课题组前期已提出了仿生叶轮推进器，并开展了初步的叶片结构设计和分析[18-19]。

本文进一步针对蛇怪蜥蜴踏水过程中脚掌的转动变化，提出一种变角度的水面矢量推进器；通过平板与轮辐的夹角变化实现驱动力矢量输出，结合转速控制提高驱动调节能力。为获取推进器的三维驱动输出性能，建立流体动力学模型，研究运动参数和结构参数对托举力、推进力和转矩的影响；进行推进器敞水试验，结合高速流场分析验证数值计算模型的正确性。

1 结构仿生设计

基于蛇怪蜥蜴的踏水运动，前期整体结构固连的仿生叶轮推进器初步增加了托举力和转矩输出。然而，在蛇怪蜥蜴踏水时，脚掌平面相对小腿的角度在时刻变化，以此调整托举力、推进力和转矩的输出，满足托起体重、推动身体和维持前倾奔跑姿态的需求变化[9]，其运动姿态如图1a所示。

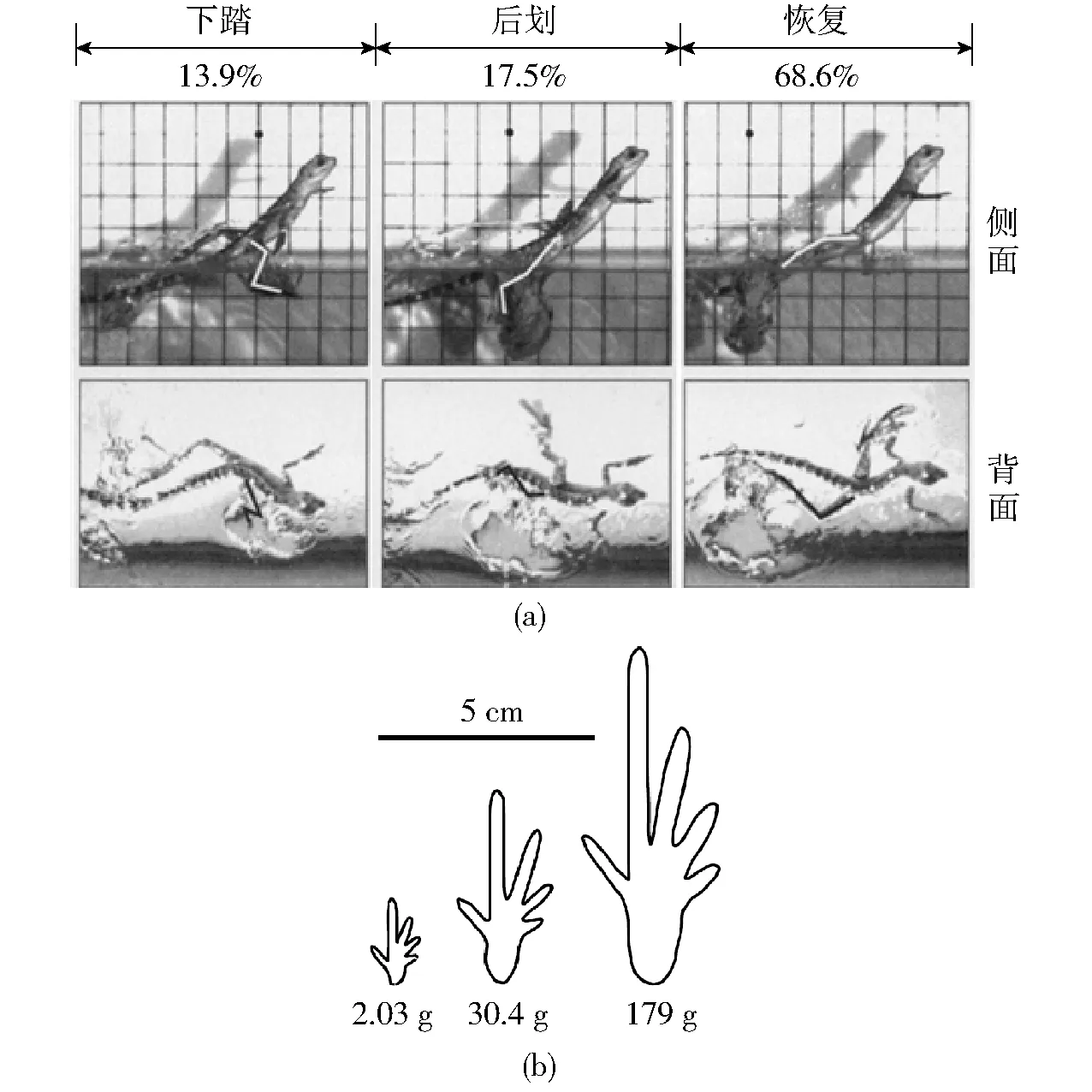
图1 蛇怪蜥蜴踏水运动姿态变化和脚掌结构图Fig.1 Kinematic phases of a stride and foot structure of basilisk lizard

不同质量的蛇怪蜥蜴脚掌平面(含脚趾)均近似长方形，如图1b所示。基于脚掌与水流的相互作用，通过姿态角的变化，蛇怪蜥蜴实现了踏水驱动力的矢量输出，其中后腿关节处肢体角度一个运动周期内的变化如图2所示。

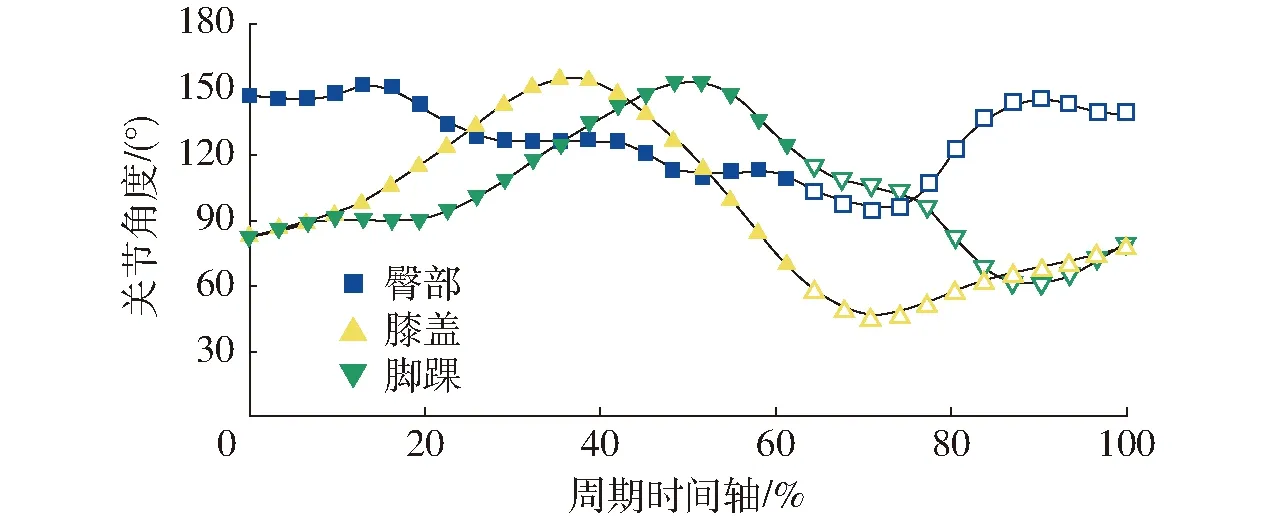
图2 腿部关节角度Fig.2 Angular excursions of limb joints

模仿蛇怪蜥蜴脚踝处脚掌绕小腿的转动行为，以旋转运动代替往复踏水，本文提出了一种变角度水面矢量推进器。推进器由叶片、伸缩杆、轮辐和轮毂组成，如图3所示。其中，近似脚掌的长方形叶片与轮辐末端铰接，伸缩杆连接轮辐和叶片，通过长短伸缩调整叶片与轮辐的夹角θ，如同脚掌与小腿夹角θ1的改变，控制叶片的拍水角度。

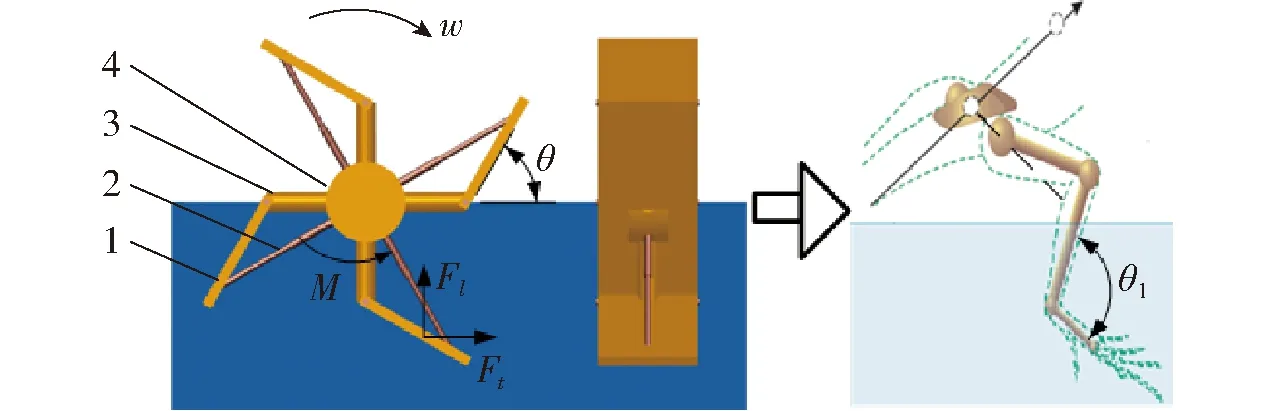
图3 变角度水面矢量推进器Fig.3 Water-surface vector propeller of variable angle1.叶片(长度0.06 m，宽度0.05 m) 2.伸缩杆 3.轮辐(含轮毂，长度0.05 m) 4.轮毂

结合叶片夹角和转速参数调节，实现仿生推进器托举力Fl、推进力Ft和转矩M的高效输出，对应方向如图3所示。因推进器传动难以实现高频转动过程中夹角θ的实时快速变化，所以本文更侧重角度调整稳定后的持续转动性能。

为验证推进器的三维驱动输出特性，开展了2对推进器的反向转动试验，尺度近似比例增大的原理样机采用0.3 m×0.2 m叶片，转速均为1.5 r/s。由图4静止和转动状态对比可看出，样机被托起了0.2 m，验证了托举力的存在；中部0.03 m×0.03 m截面的2.5 mm厚不锈钢管向内侧下方折弯，验证了转矩的存在；因2对推进器的推进力相互抵消，没有水平位移。

图4 矢量推进器反向转动试验Fig.4 Reverse rotation tests of vector propeller

伴随着气穴生成与溃散的流场变化，通过脚掌转动和踏水频率的调控，蛇怪蜥蜴踏水高效地获得了三维驱动力，实现了敌害躲避。而要进一步研究矢量推进器的驱动输出性能，也应结合流场变化，对应不同的参量，开展流体动力学分析。

2 数值计算模型

首先，通过理论分析获取影响推进器三维驱动输出的参数变量；然后，建立流体动力学模型，开展详细的数值计算。

2.1 理论分析

叶片平板旋转拍击水面的固液相互作用可看作水流冲击固定叶片的平板绕流。位于图5所示位置时，在叶片微元ds上，产生正向力dD、法向力dT和绕转轴的转矩dM[20]

dD=0.5CDρU2ds

(1)

dT=0.5CTρU2ds

(2)

dM=MdT+MdD

(3)

式中CD、CT——正向力和法向力系数

ρ——流体密度U——来流速度

ds——微元面积

MdT、MdD——正向力和法向力对轮轴的转矩

图5 叶片受力分析Fig.5 Force analysis model of blade

经坐标变化，微元ds受到的作用进一步表示为推进力dFax、托举力dFay和转矩dM

dFax=-dTsinα+dDcosα

(4)

dFay=dTcosα+dDsinα

(5)

dM=dFaxksinβ+dFaykcosβ=

dTcos(α+β)+dDsin(α+β)

(6)

式中α——正向力与水平轴的夹角

β——微元与轮轴连线的转角

k——微元到转轴的力臂

推进器的三维驱动输出可由4个叶片上的微元积分求和获得。由式(4)～(6)可得：三维驱动输出是U、β的函数，而U、β又分别与推进器转速、叶片轮辐夹角直接相关，同时结构参数也是重要的影响因素。

2.2 流体动力学模型

建立流体动力学模型，分析运动参数(转速w和叶片夹角θ)和结构参数(轮辐长度l、轮毂宽度b和轮毂直径d)对三维驱动输出的影响，如图6所示。

图6 结构参数示意图Fig.6 Schematic of structure parameters

基于k-εRNG湍流模型，应用PISO算法和流体体积法跟踪叶片水面转动的流固耦合作用。在不可压非定常流动假设的基础上，任一单元的流体体积分数方程、密度方程、粘度方程、连续方程、动量方程为

αw+αa=1

(7)

ρ=αwρw+αaρa

(8)

μ=αwμw+αaμa

(9)

(10)

(11)

式中αw、αa——水和空气在单元中所占体积比

ρw、μw、ρa、μa——水、空气密度和粘度

ui、uj——速度分量均值(i、j=1,2,3)

p——压力均值

μ——流体粘性系数

Si——广义源项

推进器轮轴位于液面，流体计算域尺寸为3 m×1 m×1 m。采用向边界等比放大的方式优化网格，推进器表面网格尺寸为0.005 m，如图7所示。计算域上侧为空气，下侧为水。

3 性能分析

基于流体动力学模型，数值计算了运动参数和结构参数对三维驱动输出的影响。基础参数：叶片夹角60°；转速1 r/s；轮辐长度0.05 m(含轮毂)；轮毂宽度0.02 m；轮毂直径0.04 m；叶片尺寸0.06 m×0.05 m×0.005 m。

3.1 叶片夹角

设定叶片夹角在-90°～90°之间变化(图6中夹角θ水面上取正值、水面下取负值)，其中6个不同角度的三维驱动输出曲线如图8所示。从图8可看出，驱动输出呈周期性变化，频率为4 Hz，这是因为4个叶片依次入水产生了周期性的流固耦合作用；驱动幅值随着角度的变化先增大后减小，推进力、托举力和转矩分别在0°、-20°和0°取得最大幅值。

最大幅值出现在0°附近是因为此时叶片与旋转方向呈约90°，叶片与水流相互作用剧烈，随着角度增大或减小，都对流固耦合作用形成了缓冲。相互作用强度可由图9流场压力反映，左下侧叶片处流场压力0°时大部分超过1 200 Pa，而-50°和50°时经过缓冲大部分在1 000 Pa左右。

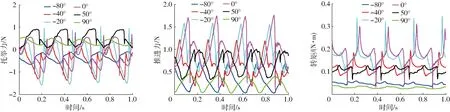
图8 不同角度驱动输出曲线Fig.8 Force characteristic curves at different angles

图9 流场压力Fig.9 Fluid pressure at different angles

以1 s时间内驱动力和转矩的平均值作为特征值进行推进器驱动输出性能分析。三维驱动随角度的变化如图10所示，随角度增大托举力先减小后增大为正值再减小；推进力和转矩先增大后减小，在0°夹角时取得最大值。

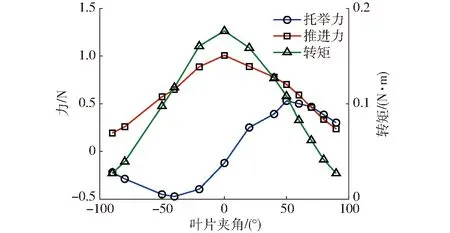
图10 驱动性能随叶片夹角变化曲线Fig.10 Curves of driving properties changing with blade angle

由图10同时可看出，θ<0°时，托举力为负值，推进器下压平台，会增大浸湿面积而增大阻力；0°<θ<40°时，托举力由负值逐渐向正值增加，但数值较小；θ>60°时，推进力和转矩迅速下降，数值较小。综合托举力、推进力和转矩输出变化，得：40°≤θ≤60°时，三维驱动输出均衡，没有过小项，所以常态航行时夹角应设置在此区间。

进一步得到了驱动力的矢量输出角，即托举力和推进力合力的夹角，如图11所示。由图11可看出，随叶片角度从0°至90°增大，驱动力输出角从-6.85°连续增加至51.95°，实现了驱动力输出的矢量变化，可根据航态匹配驱动力需求。

图13 流场压力随轮辐长度变化图Fig.13 Changing diagrams of fluid pressure with different spoke lengths

图11 驱动力输出角随叶片夹角变化曲线Fig.11 Curve of driving force angle changing with blade angle

3.2 轮辐

轮辐长度l(含轮毂部分)从0.02 m依次增加0.01 m至0.10 m，得到了9组三维驱动输出特征值(li，Fi)，i=0,1,…,8，如图12所示。由图12可看出，三维驱动随着轮辐长度的增加而增加。这是因为，同转速下，叶片上任一点的速度随着轮辐长度增加而提高，因而与水流的相互作用加强，如图13中压力场所示。由图13可看出，轮辐长度从0.02 m增加到0.10 m，前侧入水叶片压力由750 Pa提升至1 250 Pa，后侧叶片压力由部分750 Pa提升至全部1 000 Pa。

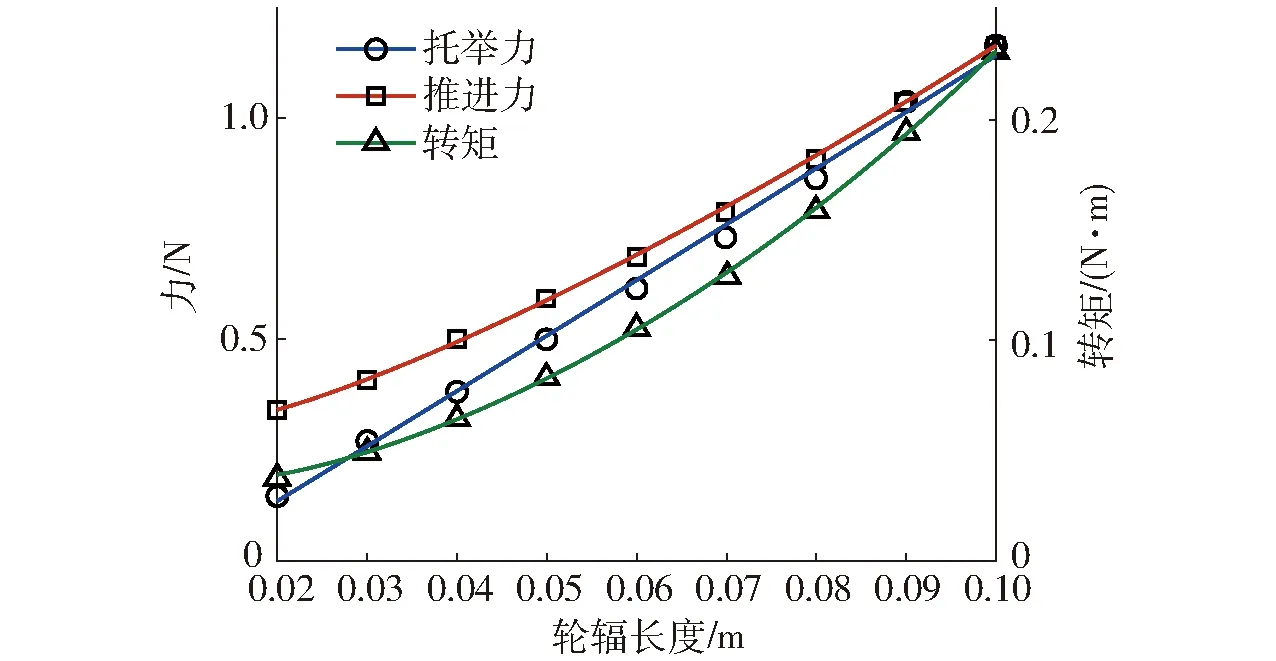
图12 驱动性能随轮辐长度变化曲线Fig.12 Curves of driving properties changing with spoke length

(12)

3.3 转速

转速的提高增加了固液作用的频率，其中3、5、7 r/s的力学特性曲线如图14所示。可以看出，3 r/s和7 r/s时驱动周期性输出的频率均为转速的4倍，但是5 r/s转速时输出的频率为转速的2倍。

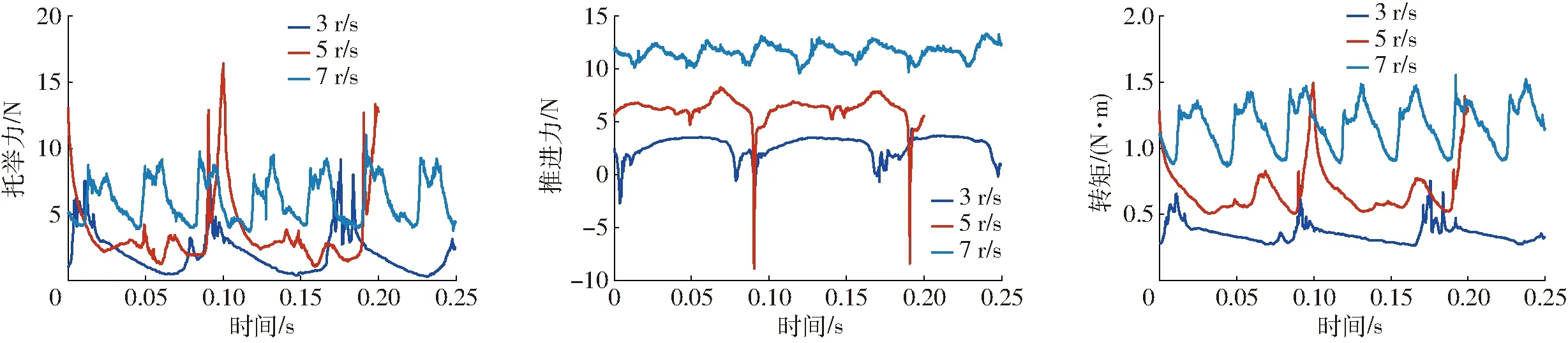
图14 不同转速下的力学特性曲线Fig.14 Force characteristic curves at different rotation velocities

频率变化是因为在低转速下，流场在下一叶片拍击之前即可恢复，随着转速提高至5 r/s左右，固液作用频率加快，而下一叶片到来时流场来不及恢复，2个叶片作用过程是一个流场恢复周期；如图15a、15b中前侧入水叶片相互作用的流体较多，而图15c、15d中下一叶片入水相互作用的流体较少。当转速进一步加快，叶片与水流相互作用的位置向下移动，静压力增加加快了流场的恢复速度，输出的频率又变回为转速的4倍。

转速由1 r/s向7 r/s增加，三维驱动输出性能如图16所示。由图16可看出，托举力、推进力和转矩分别由1 r/s时的0.50 N、0.59 N、0.083 N·m，增加至7 r/s时的6.09 N、11.61 N、1.17 N·m；三维驱动输出随着转速的增加而快速增加，驱动输出存在较大的调节范围。

图15 5 r/s转速下两相流分布图Fig.15 Water volume color contours of propeller when w=5 r/s

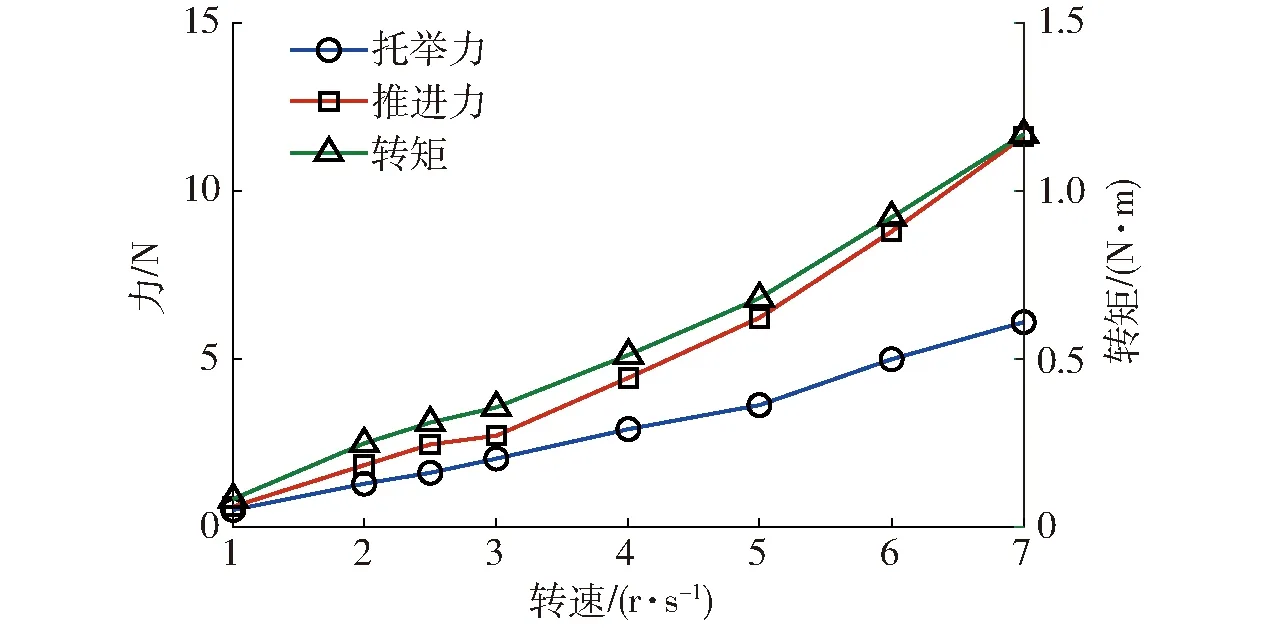
图16 驱动性能随转速变化曲线Fig.16 Curves of driving properties changing with rotation velocity

3.4 轮毂

宽度和直径是圆柱形轮毂的2个结构参数。当宽度由0.01 m向0.05 m增加时，托举力减小、而推进力和转矩在0.60 N和0.083 N·m左右浮动，如图17所示。以0.02 m宽和0.04 m直径参数为基准，推进力和转矩的数值浮动均小于6%，影响不大。

图17 驱动性能随轮毂宽度变化曲线Fig.17 Curves of driving properties changing with width of hub

当直径由0.02 m增加至0.08 m时，托举力随着直径的增加而减小，如图18所示。推进力和转矩小幅浮动，分别较直径为0.04 m时的数值最大变化了7.8%和5.4%。

图18 驱动性能随轮毂直径变化曲线Fig.18 Curves of properties changing with diameter of hub

4 推进器试验

为了验证数值计算的正确性，搭建了推进器试验系统。试验系统由推进器、水平导轨与传感器、竖直导轨与传感器和传动系统组成，如图19所示，结构参数同数值计算模型。

图19 矢量推进器试验系统Fig.19 Test system of vector propeller1.导轨 2.推进器 3.水平力传感器 4.滑块 5.传动系统 6.竖直力传感器

测得2.5 r/s转速下的托举力和推进力曲线，与数值计算结果对比，如图20所示。由图20可看出，试验曲线与数值计算结果作用力变化频率均为10 Hz，是转速的4倍。托举力和推进力试验平均值分别为2.13 N和1.95 N；数值计算托举力为2.41 N，较试验值高13.2%；数值计算推进力为1.60 N，较试验值低17.9%，误差在合理的范围内。

图20 力学特性对比曲线Fig.20 Contrasts of force characteristic

数值计算与试验曲线中，托举力的波峰和推进力的波谷位置一致。但是试验曲线托举力峰值小、凸起时间长，推进力峰值大但凸起时间短，作用力曲线未完全对应是因为：在试验中采用电动机驱动，不能保证恒角速度转动，在一个作用周期内角速度有所起伏。

进一步测试了不同转速条件下的托举力和推进力变化，如图21所示，可得：驱动力输出随着转速的增加而增加，数值计算值与试验值符合较好。

图21 驱动力随转速的变化曲线Fig.21 Curves of driving forces changing with rotation velocity

最后，由高速摄像机获取了转速为5 r/s时的推进器流场，如图22所示。流场中黑色部分为轮辐和叶片，叶片刚刚经过的区域产生了负体积的气穴，如图中三角形所在区域；叶片与流体的相互作用，一次大体积水流相互作用后紧接着一次小体积水流相互作用，2个叶片拍水过程是一个流场恢复周期，相互作用的流体体积如图22中环形所示，与图15所示数值计算流场结果一致。

图22 推进器试验流场Fig.22 Fluid fields of propeller test

5 结束语

以蛇怪蜥蜴为仿生对象，设计了变角度仿生矢量推进器，通过角度和转速调节，为水面平台提供三维驱动矢量输出，获得了减阻提速的新思路。进一步建立流体动力学模型，扩展了平板与水流相互作用的数值计算研究，得到了驱动力随叶片角度调节矢量输出的角度变化范围；推导了托举力、推进力和转矩与轮辐长度的函数关系；明确了转速和轮毂结构参数对三维驱动输出的影响规律。最后通过试验验证了数值计算模型的正确性。

1 薛军. 水陆两栖车发展史[J]. 上海汽车,2001(7):46.

XUE Jun. Development history of amphibious vehicle[J].Shanghai Auto,2001(7):46. (in Chinese)

2 杨楚泉. 水陆两栖车辆原理与设计[M]. 北京:国防工业出版社,2003.

3 辛志坡,王伟. 高速水陆两栖车辆技术发展[J]. 专用汽车,2007(6):18-21.

XIN Zhipo, WANG Wei. Technology development of high-speed amphibious vehicle[J]. Special Purpose Vehicle, 2007(6):18-21. (in Chinese)

4 邓锐, 黄德波, 周广利, 等. 带有阻流板的双体船水动力性能数值研究[J]. 华中科技大学学报:自然科学版,2011,39(4):97-100.

DENG Rui, HUANG Debo, ZHOU Guangli, et al. Numerical research on hydrodynamics performances of catamarans with interceptors[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition,2011,39(4):97-100. (in Chinese)

5 唐建飞, 杨帅. 高速艇水翼减阻方案及翼滑艇阻力估算方法[J]. 船舶力学,2015,19(1-2):69-77.

TANG Jianfei, YANG Shuai. Drag reduction regime by hydrofoil and resistance estimation method for gliding-hydrofoil craft[J]. Journal of Ship Mechanics, 2015,19(1-2):69-77. (in Chinese)

6 钟本基, 倪其军, 刘玉川. 动力增升降阻技术在快速船上的应用[J]. 中国造船,2008,49(1):11-18.

ZHONG Benji, NI Qijun, LIU Yuchuan. Technology on dynamic enhancing lift & dropping resistance and its using in high speed craft[J]. Shipbuilding of China, 2008,49(1):11-18. (in Chinese)

7 孙华伟. 滑行面形状对滑行艇阻力与航态影响数值分析[D]. 哈尔滨:哈尔滨工程大学,2012.

SUN Huawei. Numerical analysis of planning-hull surface shape on resistance and sail attitude[D]. Harbin:Harbin Engineering University,2012. (in Chinese)

8 剧冬梅, 项昌乐, 周鹏飞, 等. 纵倾角对轻型轮式两栖车辆的阻力特性影响研究[J]. 兵工学报,2015,36(1):19-26.

JU Dongmei, XIANG Changle, ZHOU Pengfei, et al. Analysis of the effect of trim angle on the resistance characteristics for wheeled amphibious vehicle[J]. Acta Armamentatii,2015,36(1):19-26. (in Chinese)

9 HSIEH S T, LAUDER G V. Running on water: three-dimensional force generation by basilisk lizards[J]. PNAS,2004, 101(48):16784-16788.

10 GLASHEEN J, MCMAHON T. Size-dependence of water-running ability in basilisk lizard[J]. The Journal of Experimental Biology,1996, 99(12):2611-2618.

11 徐林森, 魏鲜明, 曹凯. 仿生双足水上行走机器人优化设计及控制方法[J]. 机械工程学报,2014,50(15):12-18.

XU Linsen, WEI Xianming, CAO Kai. Optimization design and control method of biped robot running on water[J]. Journal of Mechanical Engineering, 2014,50(15):12-18. (in Chinese)

12 XU Linsen, MEI Tao, WEI Xianming, et al. A bio-inspired biped water running robot incorporating the Watt-I planar linkage mechanism[J]. Journal of Bionic Engineering,2013,10(4):415-422.

13 PARK H, FLOYD S, SITTI M. Roll and pitch motion analysis of a biologically inspired quadruped water runner robot[J]. The International Journal of Robotics Research,2010,29(10):1281-1297.

14 FLOYD S, ADILAK S, RAMIREZ S, et al. Performance of different foot designs for a water running robot[C]∥IEEE International Conference on Robotics and Automation, 2008:19-23.

15 KIM H, JEONG K, SEO T. Analysis and experiment on the steering control of a water-running robot using hydrodynamic forces[J]. Journal of Bionic Engineering,2017,14(1):35-46.

16 KIM H, SITTI M, SEO T. Tail-assisted mobility and stability enhancement in yaw and pitch motions of a water-running robot[J]. IEEE/ASME Transactions on Mechatronics,2017,22(3):1-11.

17 黄涣青. 内河小型清洁船明轮推进研究[D]. 镇江:江苏科技大学,2013.

HUANG Huanqing. Study on paddle wheel propulsion of the water clean boat[D]. Zhenjiang:Jiangsu University of Science and Technology,2013. (in Chinese)

18 白向华,吕建刚,郭劭琰,等.基于蛇怪蜥蜴踏水机理的仿生叶轮负载性能分析[J].华中科技大学学报:自然科学版,2015,43(2):76-80.

BAI Xianghua, LÜ Jian’gang, GUO Shaoyan, et al. Performance analysis of bionic impeller under different loads based on mechanism of basilisk lizard treading water[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2015, 43(2):76-80. (in Chinese)

19 张仲志, 吕建刚, 宋彬, 等. 水面矢量推进器仿生设计与试验[J/OL] 农业机械学报,2016,47(10):405-412.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20161053&flag=1.DOI：10.6041/j.issn.1000-1298.2016.10.053.

ZHANG Zhongzhi, LÜ Jian’gang, SONG Bin, et al. Bionic design and experiment of water-surface vector propeller[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2016,47(10):405-412. (in Chinese)

20 CHRISTINA G, MEYER N, MARTIN B. Simulation of an underwater hexapod robot[J]. Ocean Engineering, 2009,36(1):39-47.