气动柔性关节仿生六足机器人步态规划与运动性能研究

赵云伟 耿德旭 刘晓敏 刘荣辉 刘 齐

(1.北华大学工程训练中心， 吉林 132021； 2.北华大学机械工程学院， 吉林 132021)

0 引言

与轮式和履带式机器人相比，足式机器人采用足部与地面点接触的方式运动，具有更好的灵活性和机动性，适于在农田等复杂地面行走[1-3]，可用于农作物的采摘、托运和检测等。常见的足式机器人多采用四足、六足和多足形式，以电动机和液压驱动为主[4-6]。FRED等[7]研制了一种类似昆虫的仿生六足机器人，该机器人仿照美洲螳螂外形，采用类似螳螂的腿部结构。印度国家技术研究所针对六足地面移动机器人中建立了静力学和动力学模型，进行了行走稳定性和能量消耗、转向步态规划及实时控制策略研究[8-11]。韩国成均馆大学研制了带有视觉传感系统、可在复杂环境下行走的四足机器人[12]。荣誉等[13-14]将并联机构用于腿部结构，设计了一种用于山地、林地和丘陵等环境的农业六足机器人，并对该机构进行了静力学和运动学分析，建立了位置逆解模型与速度映射方程。文献[15]阐述了一种中心对称的六足机器人，并依据螺旋理论和指数乘积方程建立了动力学模型，进行了运动性能分析。哈尔滨工业大学研制了大尺度重载液压驱动六足机器人，研究了腿长比例对步行速度和关节速度的影响，并提出一种减小足地接触冲击的足端轨迹规划[16-17]。

上述国内外学者研制的足式机器人的腿部结构多采用分段刚性结构或并联结构，缺乏类似生物肌肉的柔顺性和灵活性[18]。而气动人工肌肉在柔顺性方面具有生物肌肉特性，适于作为仿生机器人的关节和执行机构[19]。目前气动人工肌肉驱动的足式机器人研究和应用较少，尚无采用柔性关节直接驱动的六足机器人。为扩展人工肌肉在地面移动机器人中的应用，本文采用自主研发的气动多向弯曲柔性关节设计一种六足地面移动机器人，关节直接应用于机器人腿部，驱动机器人运动。为实现机器人的自由移动，需要合理地规划其步态。针对该机器人的腿部柔性关节的形变特性，采用“三角步态”原理规划行进和转弯步态，并建立其运动学模型，采用3D运动捕捉系统测试机器人的运动性能。

1 六足机器人结构与关节建模

1.1 结构与运动原理

文中研制的气动六足机器人主要由本体和腿部组成，其结构如图1所示。该机器人本体仿照爬行类昆虫(蜘蛛)外形，腿部对称分布于身体两侧。机器人的腿部由气动多向弯曲柔性关节(大腿)、小腿和足部组成，其中柔性关节在气压下产生变形，可模拟昆虫腿部伸展和弯曲动作。该机器人采用外置控制系统，具有18个自由度和12个机动度，负载能力为0.5 kg。通过气压控制系统协调腿部运动，实现前进、平移和转弯等功能。

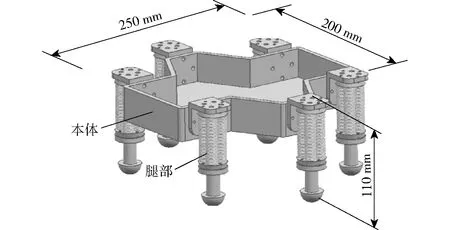
图1 六足机器人结构Fig.1 Structure of bionic hexapod robot

1.2 柔性关节模型

1.2.1结构与功能

多向弯曲柔性关节属于气动复合弹性体，主要由4根伸长型人工肌肉并联组成(图2)。人工肌肉内部为弹性橡胶气囊，外部设有圆柱螺旋弹簧可束缚胶囊径向变形。通入压缩气体后，人工肌肉内壁受压膨胀，压力气体在驱动器端盖部产生作用力驱动关节变形。通过控制关节内不同肌肉的内腔压力，柔性关节可向空间多方向弯曲和轴向伸长。

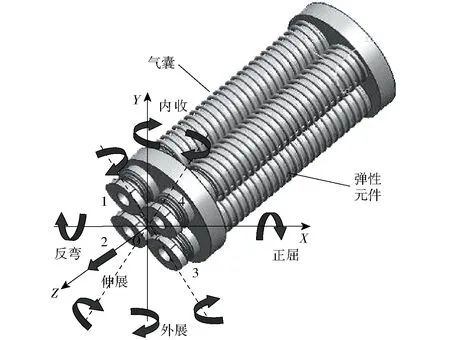
图2 多向弯曲柔性关节结构Fig.2 Structure of multidirectional bending joints

人工肌肉通入气压pi=p，i=1、2、3、4为人工肌肉编号(图2)。根据关节的变形，机器人腿部的动作模式4种：p1=p，p2=p3=p4=0时的斜侧向弯曲摆动；p1=p2=p,p3=p4=0或p1=p4=p,p2=p3=0时的外展或正屈运动；p1=p2=p3=p,p4=0时的斜侧向弯曲摆动；p1=p2=p4=p3=p时的轴向伸展运动。

机器人腿部气压控制系统由4个电磁换向阀控制和1个电气比例阀组成，其控制原理如图3所示。通过PLC控制电气比例阀调整关节内肌肉的充气压力，控制关节形变量；通过控制各个电磁换向阀的通断控制关节内肌肉的充气状态，完成设定工作模式下的动作。

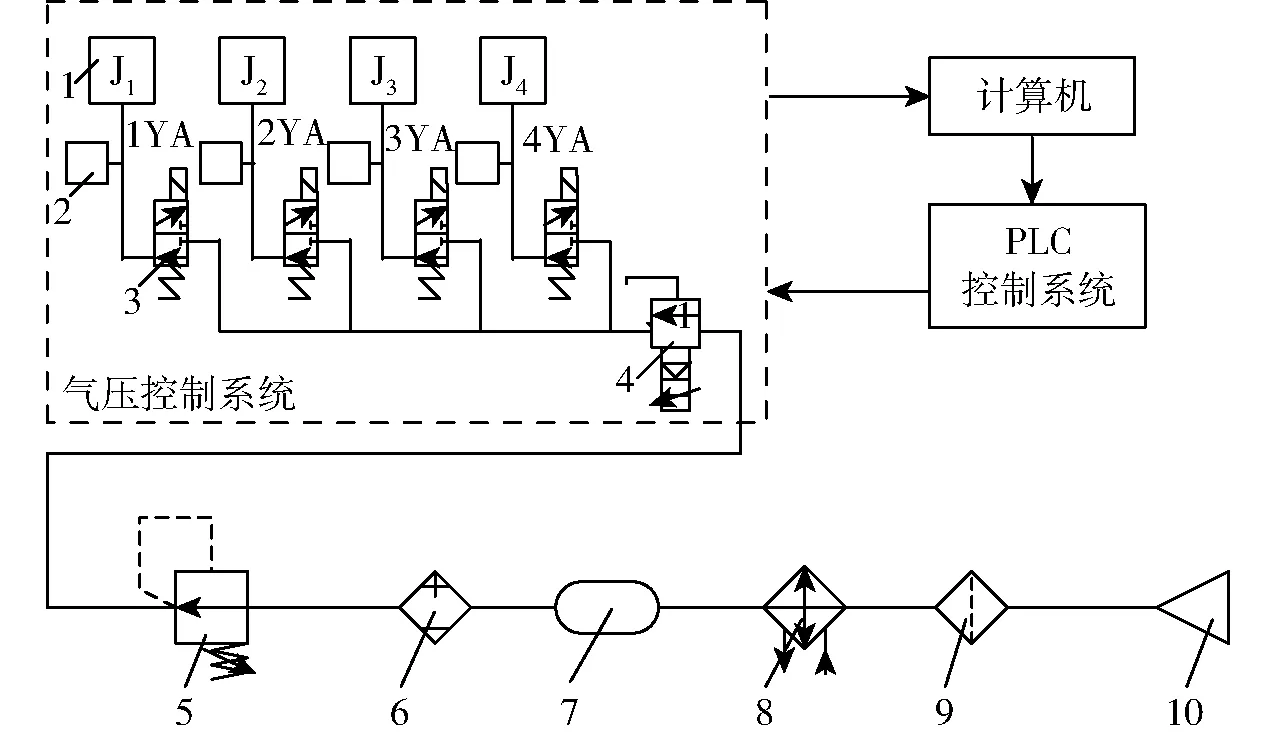
图3 机器人腿部控制原理图Fig.3 Control principle diagram of robot leg1.人工肌肉 2.气压传感器 3.电磁阀 4.比例阀 5.精密减压阀 6.空气干燥器 7.储气罐 8.冷却器 9.过滤器 10.气压源

在关节内肌肉不同通气组合方式下，机器人腿部的动作模式，如图4所示。在柔性关节的驱动下，机器人的腿部可实现迈腿、蹬腿、平移和抬腿等动作。

图4 机器人腿部动作模式Fig.4 Movement modes of robot leg

1.2.2受力和形变分析

施加气压后，柔性关节在端部轴向力和弯曲力矩的作用下产生伸长或弯曲变形。在变形过程中，弹簧和橡胶气囊产生相应的轴向应变和阻抗力矩(图5)。

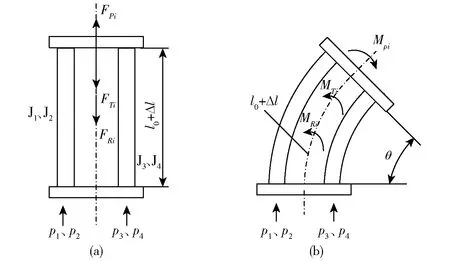
图5 关节受力分析Fig.5 Force analysis of joint

关节在压力气体的作用下沿中性层弯曲，肌肉阻碍关节弯曲变形时，除绕本体弯曲时产生的阻抗力矩外，还有绕关节弯曲中心弯曲的耦合力矩。柔性关节内人工肌肉中心对称分布于半径为r的圆周上，肌肉与中性层距离rj，j=1、2、3、4表示关节工作模式，如图6所示。关节前3种动作模式为弯曲变形。当采用J1通气工作时，弯曲中性层为Ⅱ。此时，肌肉J1伸长，其余肌肉压缩；当采用J1和J2通气工作时，弯曲中性层为Ⅰ。此时，肌肉J1和J2伸长，肌肉J3和J4压缩；当采用J2、J3和J4工作时，弯曲中性层为Ⅱ。此时肌肉J1、J2和J3伸长，肌肉J4压缩。弯曲工作状态下，人工肌肉中心到驱动器弯曲变形中性层的距离分别为r1=r3=r，r2=rsinα。

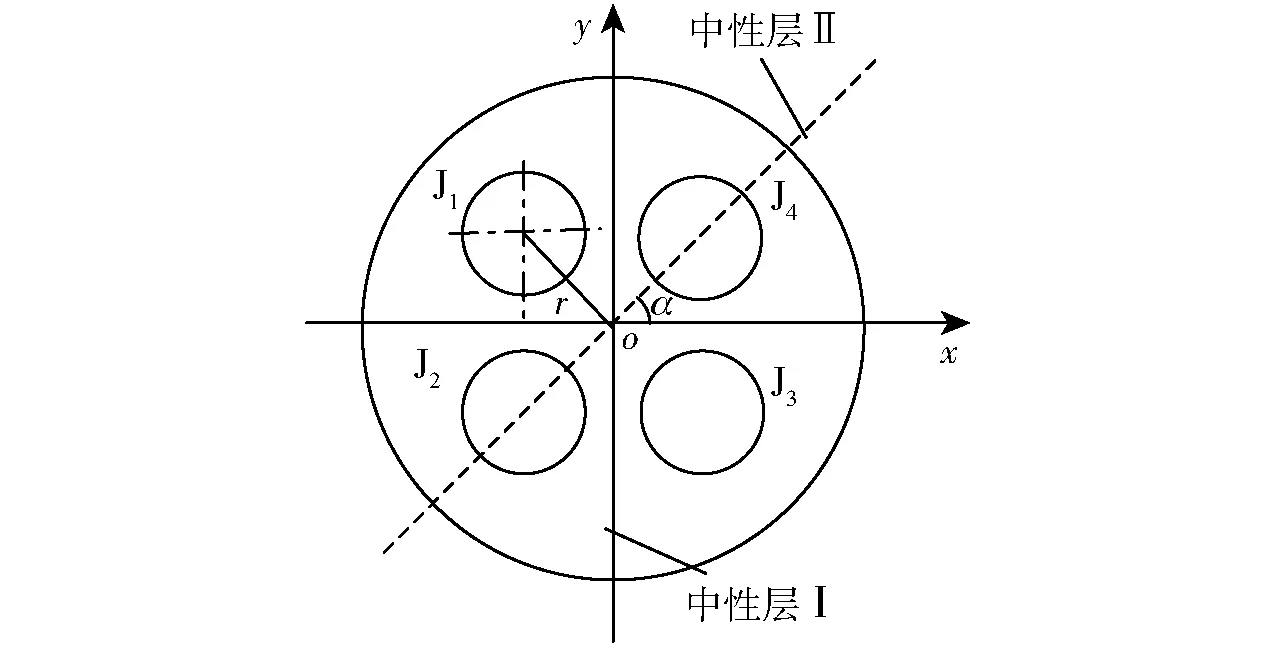
图6 肌肉和弹性骨架与中性层距离Fig.6 Distance between elastic skeleton and neutral layer

假设关节内人工肌肉轴向变形量协调同步，忽略之间耦合力影响，且变形力符合线性叠加,则在机器人腿部4种动作模式下，关节轴向伸长量[20]为

(j=1，2，3，4)

(1)

式中l0——人工肌肉有效原始长度

D1——橡胶管原始外径

D2——橡胶管原始内径

E2——橡胶管弹性模量

k1——弹簧刚度

F0——弹簧预紧力

Kj——4种动作模式下的协调系数，K1=1、K2=2、K3=3和K4=4

根据变形协调条件，假设肌肉弯曲力矩符合线性叠加，并考虑肌肉轴向产生的耦合力矩，可得关节的弯曲角度[20]为

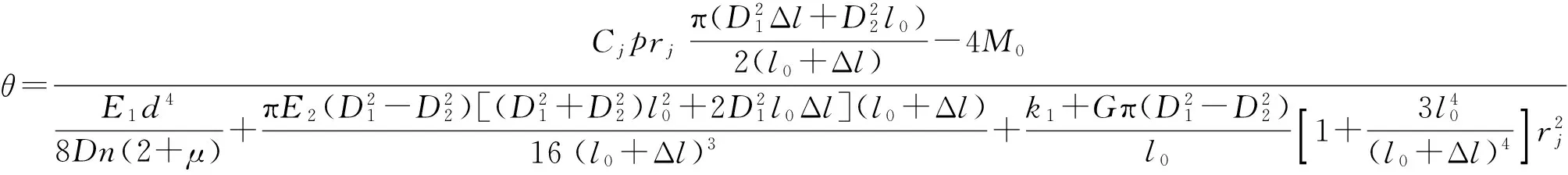
(2)

式中D——弹簧中径n——有效圈数

d——弹簧钢丝直径

E1——弹簧弹性模量

μ——泊松比

G——橡胶管剪切弹性模量

rj——人工肌肉中心到驱动器弯曲变形中性层的距离

M0——肌肉预应力产生的初始力矩

Cj——关节不同工作模式下的协调系数，C1=C3=1,C2=2

2 机器人步态规划

基于“三角步态” 原理对机器人的行进步态进行规划。机器人6条腿对称分布位于正六边形的6个顶点上。将机器人的腿部分为支撑相和摆动相。当一组行进时，另一组形成稳定的三角形支撑，两组腿部交替运动实现机器人的前行、平移和转弯。

2.1 前行步态规划

机器人前行步态共分为7步，迈腿顺序为246-135-246，如图7所示。图7中空心点表示腿部脱离地面，实心点表示腿部与地面接触。为防止迈腿时腿部与地面的干涉，机器人行进时需要一组腿部支撑地面，此时支撑相腿部关节4根肌肉同时充气伸长抬升本体(图7a)；摆动相腿部关节充气正屈，实现迈腿动作(图7b)；支撑相同时反弯，实现蹬腿动作，此时机器人前行1个步距s(图7c)；当摆动相完成迈腿后充气伸长支撑本体，此时机器人完成2个步距s移动(图7d)；支撑相与摆动相交替运动，重复上述动作，可完成一个循环4个步距前行运动。由于机器人腿部对称分布，机器人平移步态规划与前行步态类似，通过改变关节的充气方式，即可实现机器人横向移动。

图7 机器人前行步态示意图Fig.7 Gait sketch of stride forward

2.2 转向步态原理

机器人的转向步态共分为4步，迈腿顺序为246-246，如图8所示。首先支撑相腿部关节4根肌肉同时充气伸长抬升本体(图8a)；摆动相腿部关节三肌肉充气外展，顺时针或逆时针摆动(图8b)；支撑相腿部关节同时放气，此时摆动相与地面接触(图8c)；当摆动相腿部充气伸长支撑本体后，此时机器人完成一个角度的转动(图8d)；两组腿部交替运动，重复上述动作，可完成转弯运动。

图8 机器人转向步态示意图Fig.8 Gait of making a turn

3 机器人运动学建模

根据建立的机器人坐标系，采用齐次坐标变换矩阵由关节形变规律可获得足部的位置矢量。结合机器人运动步态建立其运动学建模，进而得到机器人本体位置关系，以此分析机器人的整体速度、转动角度和几何中心偏置。

六足机器人坐标系如图9所示。以机器人本体几何中心为原点建立机器人随动坐标系O(X,Y,Z)，机器人前进方向为Y向，机器人本体平面法向为Z向。在腿部安装位置建立腿部基坐标系Oi(Xi,Yi,Zi)(i=1,2,…,6，为腿的序号)，坐标轴方向与本体坐标系相同，分布在正六边形6个顶点上。取腿部6个特征点建立坐标系Oij(Xij,Yij,Zij)(j=1,2,…，6)，P(Xp,Yp,Zp)为系统固有坐标系。

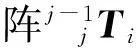
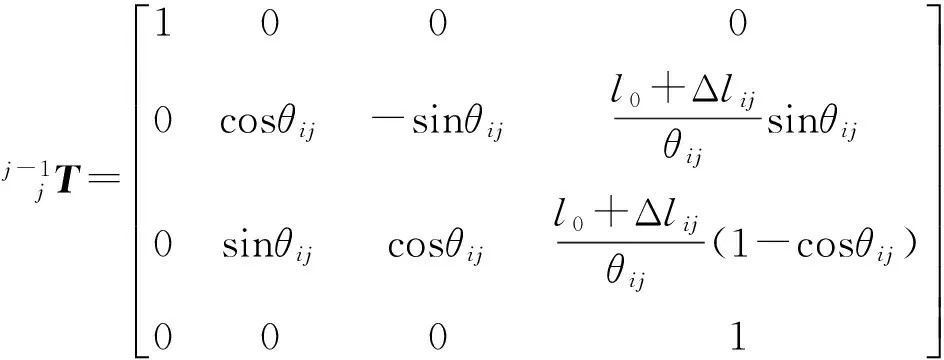
(3)

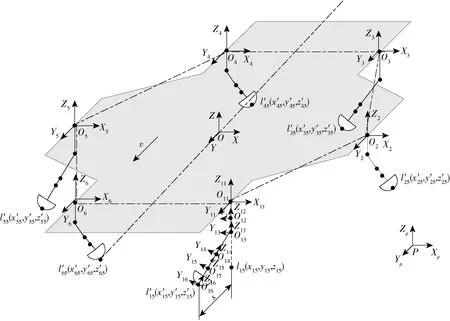
图9 机器人坐标系设置Fig.9 Coordinate system of robot

腿部任意特征点jPij在腿部基坐标系中的位置，经坐标变换可得

(4)

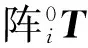
(5)

式中li——腿部位置距离几何中心的距离

γi——各腿部在本体坐标系中的分布角度

经坐标变换可得机器人腿部各关键点在随动坐标系下的位置。

(6)

设定机器人初始运动时系统固有坐标系与随动坐标系重合，则1号腿足部矢量p=[pxpypz]T为

(7)

支撑相推进本体前进的距离为机器人腿部前行步距s，为l16与l′16在y方向的距离，即

(8)

机器人按规划步态进行运动，其前行速度取决于支撑腿部推进本体前行的速度。假设机器人在运动过程中稳定，本体几何中心位置在y向距离|y′0-y0|，根据“7步法”前行步态规划，可知在一个循环周期内机器人移动位移为4s。则，在一个循环周期内机器人整体移动速度为

(9)

式中f——机器人的步频

S——机器人一个循环周期内的前行位移

T——机器人一个循环周期内的前行时间

机器人腿部分布在正六边形的6个顶点上，假设机器人转动平顺。依照“4步法”转弯步态，机器人腿部与水平呈α的方向迈步，在一个循环周期后，机器人转过一定角度且几何中心位置产生偏置(图10)。

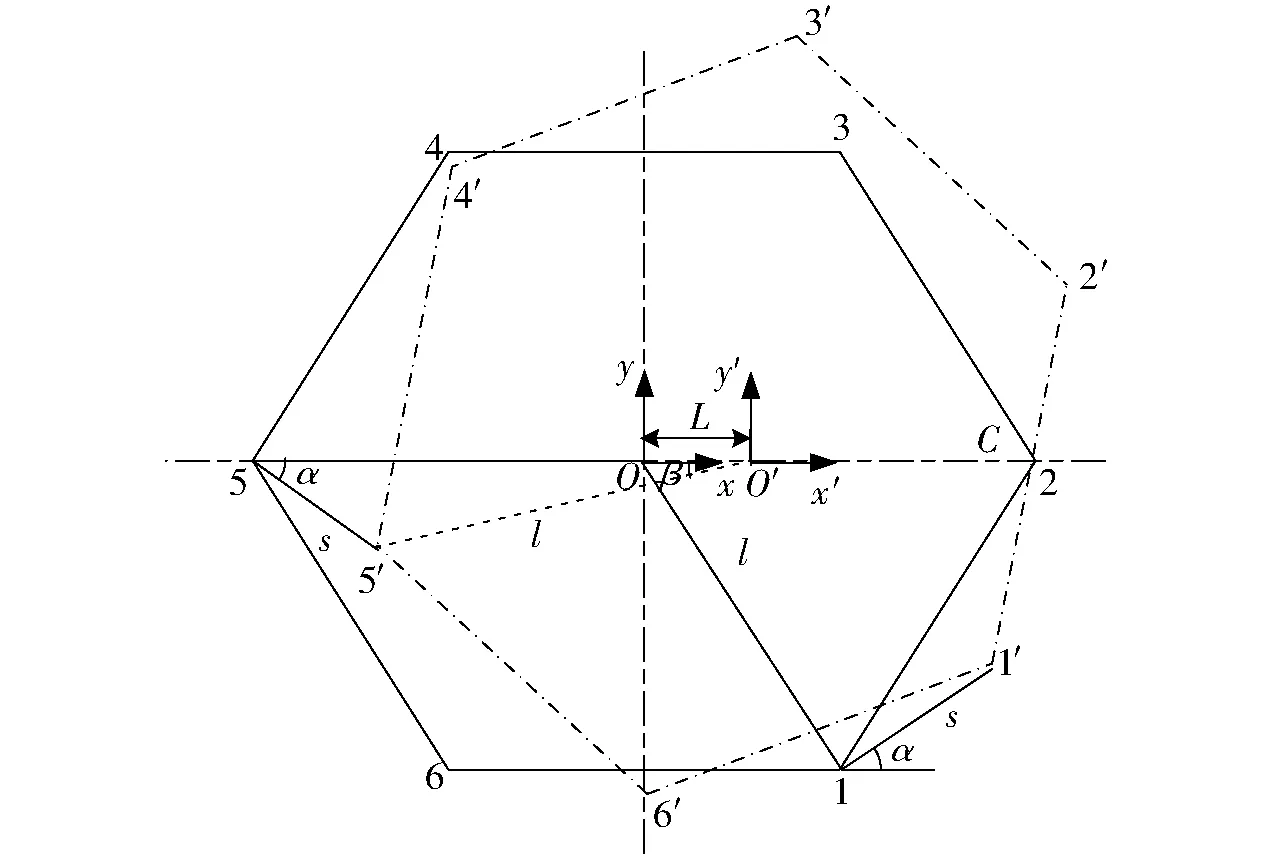
图10 机器人转角几何关系Fig.10 Geometric relation of rotation angle of robot

机器人转向后，足部的位置即为机器人移动后的本体位置，如图10所示。由转动后足部所在正六边形顶点位置与几何中心的位置关系，可知

(10)

由式(10)求解可得，首次转动后几何中心位置为

(11)

由图10所示几何关系，可知一个周期内机器人转角为

(12)

当机器人连续回转时，其移动后的位置关系如图11所示。

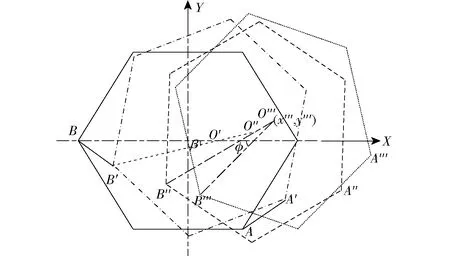
图11 机器人连续转弯Fig.11 Positions of robot after continuous turn

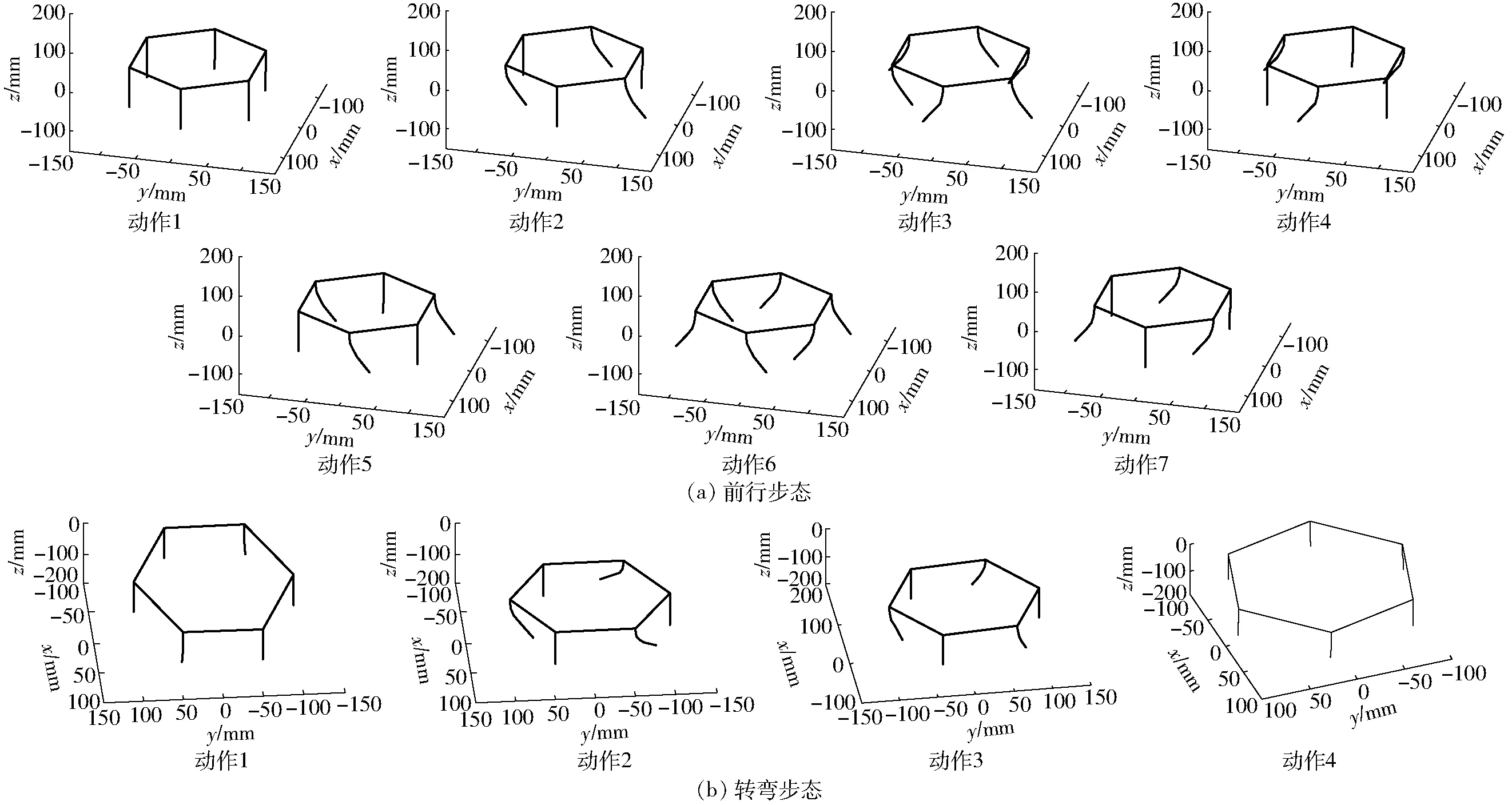
图13 机器人步态仿真Fig.13 Gait simulations of hexapod robot

由机器人运动后本体位置关系，可知其转角和转动后的中心坐标分别为

(13)

(14)

其中

L=|x′1-x0|

式中L——首次转动时的偏心距

4 步态仿真与样机实验

为验证步态规划的正确性，应用建立的运动学模型，获得6条腿及腿部关键点在各坐标系下的位置关系，在Matlab中进行了六足机器人步态仿真，并进行机器人单步行走实验。

由式(4)可得机器人腿部各关键点在腿部基坐标系下的位置(图12)。由图12可知，机器人在运动过程中，可通过调整系统气压对其迈步方式和步距进行控制，达到步态规划要求。

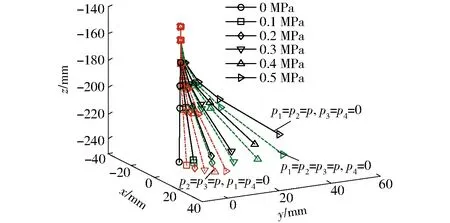
图12 机器人腿部运动轨迹Fig.12 Leg trajectory of hexapod robot

目前该机器人主要有前行、平移和转弯3种步态。工作气压0.35 MPa下，步态仿真结果如图13所示，由图13可知，机器人在前行和转弯时支撑相和摆动相腿部运动姿态。图13a为前行步态仿真，支撑相和摆动相不断切换，支撑相推进机体移动，实现机器人前行。依据规划步态前行步态由7步组成，共前行4个步距。图13b为转弯步态仿真。仿真分为4步，在腿部配合运动下，实现机器人在小范围内转动。通过步态仿真可知，机器人在行进时腿部位姿，符合步态规划要求，机器人腿部弯曲形变量和组合动作可完成预设步态。

为验证步态规划的正确性，进行机器人单步运动实验。当步频为3 Hz，工作气体压力为0.35 MPa时，机器人在一个循环周期内行进动作姿态，如图14所示。按照前行步态规划，机器人行进时完成7个动作，支撑相和摆动相交替运动，共前行100 mm，如图14a所示。图14b为机器人在一个循环周期内转动。此时关节采用3根肌肉进行通气，关节沿着45°方向侧摆，机器人转动角为20°。

图14 物理样机实验Fig.14 Experiment on hexapod robot prototype

通过步态仿真和物理样机实验可以看出，机器人能按照要求完成相应步态，可实现直线行走和转弯，具有一定的灵活性，说明基于“三角步态”法设计的前行和转弯步态的可行性和正确性。

5 实验与分析

通过静力学实验装置和运动学测试平台，分别进行了机器人腿部驱动关节的静力学实验、步态实验和机器人的运动学实验。

5.1 关节静力学实验

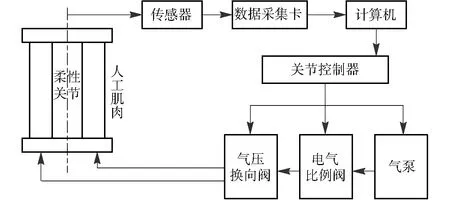
图15 气压变形综合实验台原理Fig.15 Measuring principle of experiment on deformation

采用磁致位移传感器和陀螺仪传感器等实验装置对多向弯曲关节进行了静力学实验，获得了其伸长量和弯曲角度的变化。其静力学原理，如图15所示。

关节有效长度为50 mm，直径为30 mm，质量100 g。关节参数如表1所示。

表1 人工肌肉几何参数及材料特性Tab.1 Material parameters of artificial muscle

将表1的参数代入式(1)和式(2)可得多向弯曲关节2根同侧肌肉工作时，其轴线伸长量和弯曲角随气压的变化(图16)。由图16可以看到，由于在不同压强下关节内人工肌肉驱动力不一致，关节轴线伸长量和弯曲角随着通入气体压强的增加随之呈非线性增加。经比较得关节伸长量和弯曲角的理论计算结果与实验数据趋势一致，吻合较好。关节弯曲时形变量与采用的弹簧钢丝直径成反比，与节距呈正比。轴向最大伸长率为40%，弯曲角可达60°。

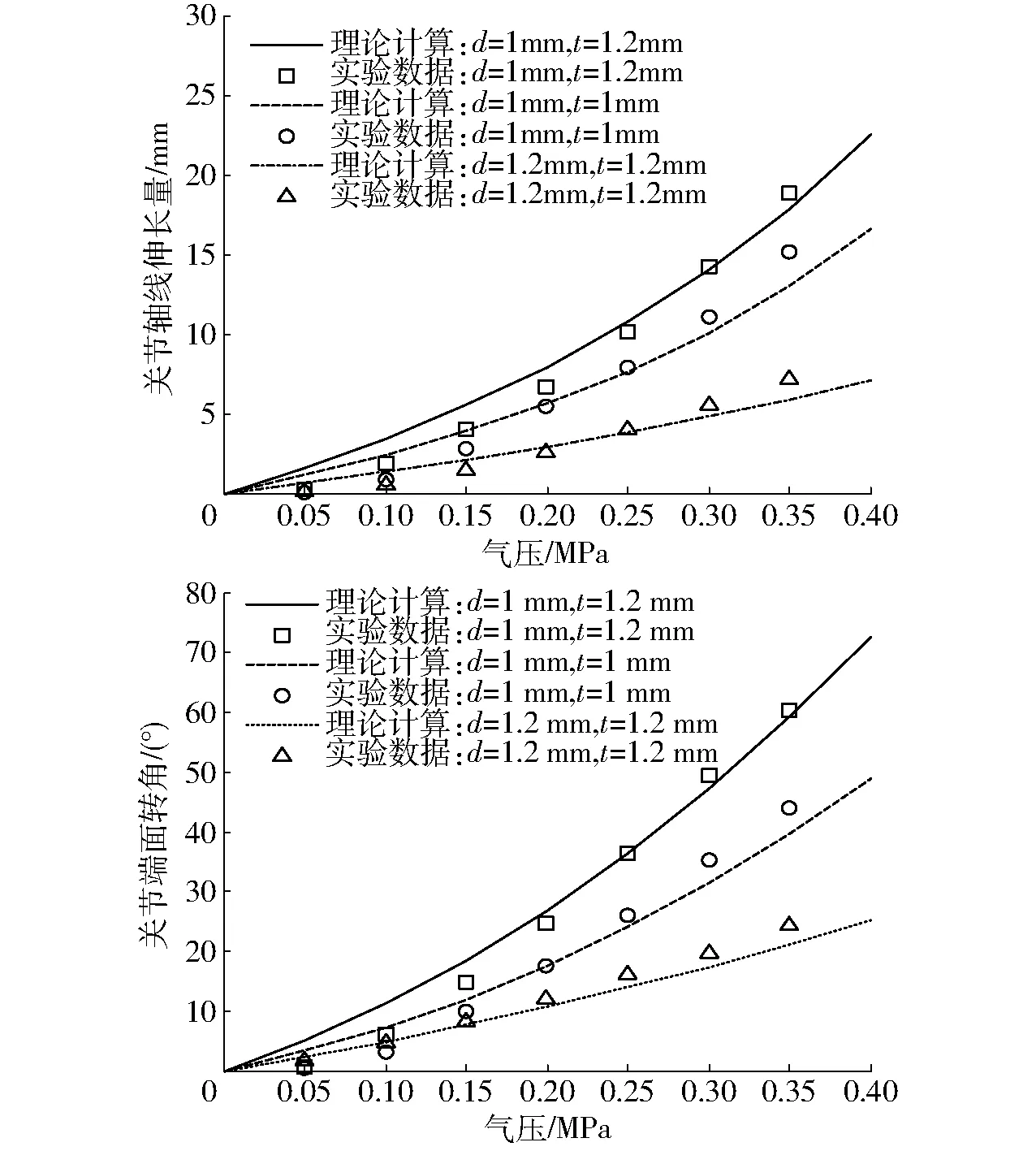
图16 关节形变量与气压的关系Fig.16 Relations between deformation and air pressure

5.2 机器人运动学实验

利用运动学测试平台进行了机器人运动学实验，获得了不同气压、动作频率和载荷下机器人移动位移、速度和重心变化及足部运动空间。图17a为机器人运动学测试原理，机器人所在平面为XY平面，Y向为机器人前行方向，Z向为机器人重心变化方向。该实验平台主要由气源、气压控制系统、PLC、Optotrak CertusTM三维运动捕捉系统组成(图17b)。通过视觉传感器捕捉安装在机器人本体和足部的标识点的空间位置信息，以此获得机器人运动时的位移变化。

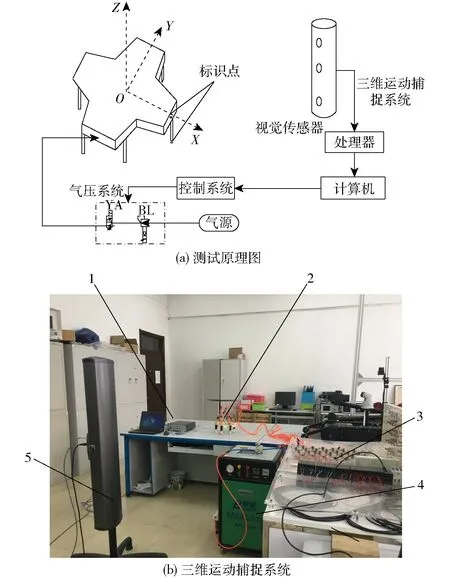
图17 机器人运动学实验平台Fig.17 Kinematics experiment of hexapod robot1.中央处理器 2.六足机器人 3.气压控制系统 4.气源 5.位移传感器

具体实验条件和关节参数，如表2所示。

表2 实验条件及材料参数Tab.2 Experimental condition and material parameters

5.2.1足部工作空间形状分析

通过3D捕捉系统采集安装在机器人足部的标记点的空间位置信息，获得0.5 MPa气压内不同通气组合方式下，机器人足部工作空间(图18)。

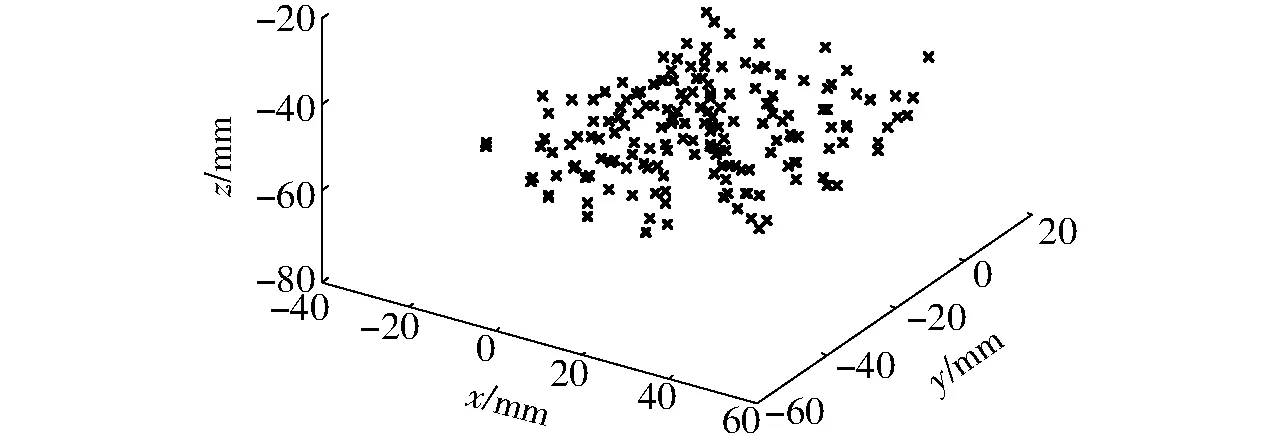
图18 机器人足部工作空间Fig.18 Work space of foot of hexapod robot

由图18可以看出，足部工作空间呈半球锥形，分布均匀合理，满足机器人腿部的步态要求。机器人腿部可向空间任意方向迈步，达到所需空间位置。

5.2.2机器人平移实验

通过足部标识点的位置变化，可获得在关节不同通气组合方式下，机器人移动时步距与气压的关系，如图19所示。由图19可知，机器人步距理论计算与实验数据趋势一致，吻合较好。随着气压增加，由于关节弯曲形变量的增加，在0.5 MPa内机器人迈步步距随之增大。当关节通入气压超过0.3 MPa后，由于采用三肌肉驱动方式关节轴向变形量显著增高，其步距略大于两肌肉驱动。通过调整关节内气体压强，可以控制机器人的前行步距。

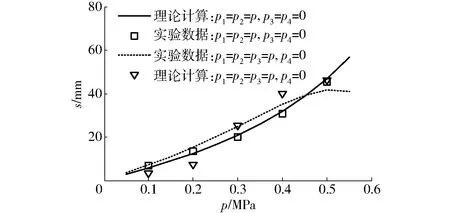
图19 步距随气压的变化曲线Fig.19 Changing curves of step and air pressure

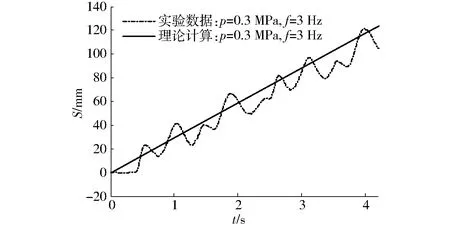
图20 机器人移动位移随时间的变化Fig.20 Changes of displacement with time

机器人前行位移随时间的变化如图20所示。由图20可以看到，依据前行步态规划，随着循环次数的增加，机器人前行位移随之递增。由于关节有一定的刚度和阻尼，及步态规划的不连续性，机器人前行时出现晃动，与理论计算相比实际前行位移存在一定超调量，机器人整体移动速度为26.7 mm/s。

5.2.3机器人转动实验

图21和图22分别为机器人在转动过程中转动角度和几何中心位置变化。依照转动步态规划，机器人转角随着循环周期的增加而随之增大。理论计算结果与达到稳态的转角吻合较好。空载时单个周期内机器人转动角为15°(图21)。

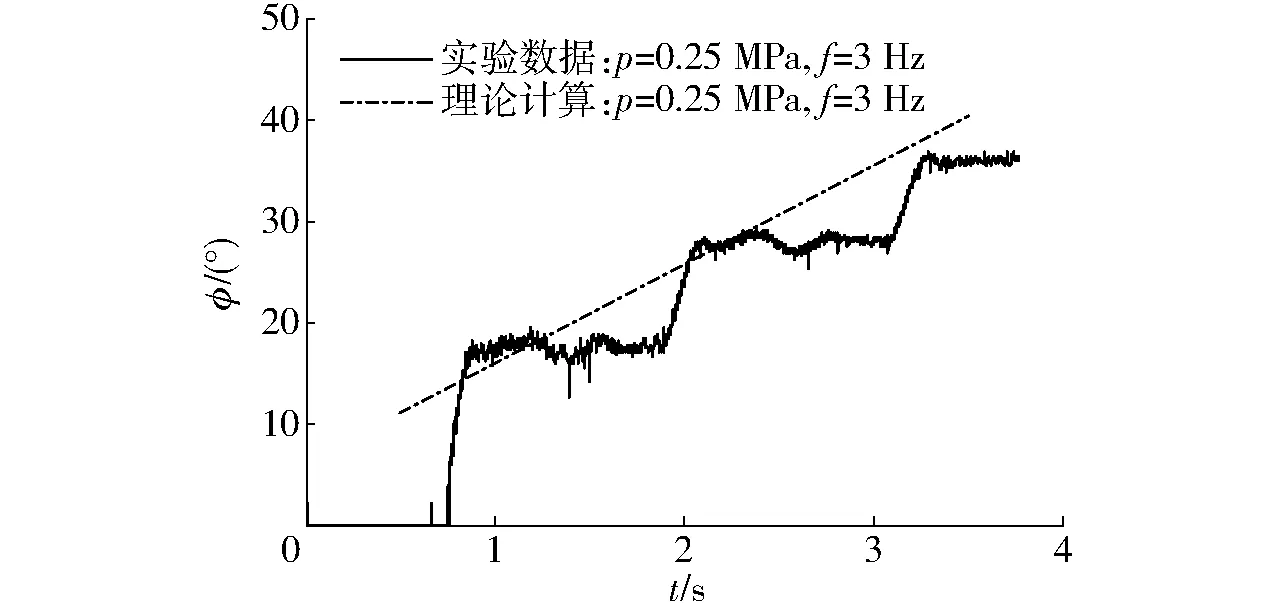
图21 机器人转角随时间的变化Fig.21 Changes of rotation angle with time

由图22可看到，采用4步法机器人转弯时，理论上其几何中心沿着圆弧线偏移，最小转弯半径为50 mm。由于机器人本身特性和步态的不一致性，机器人转动时将产生晃动，随着转动角度的增加逐渐累计，出现较大偏差。

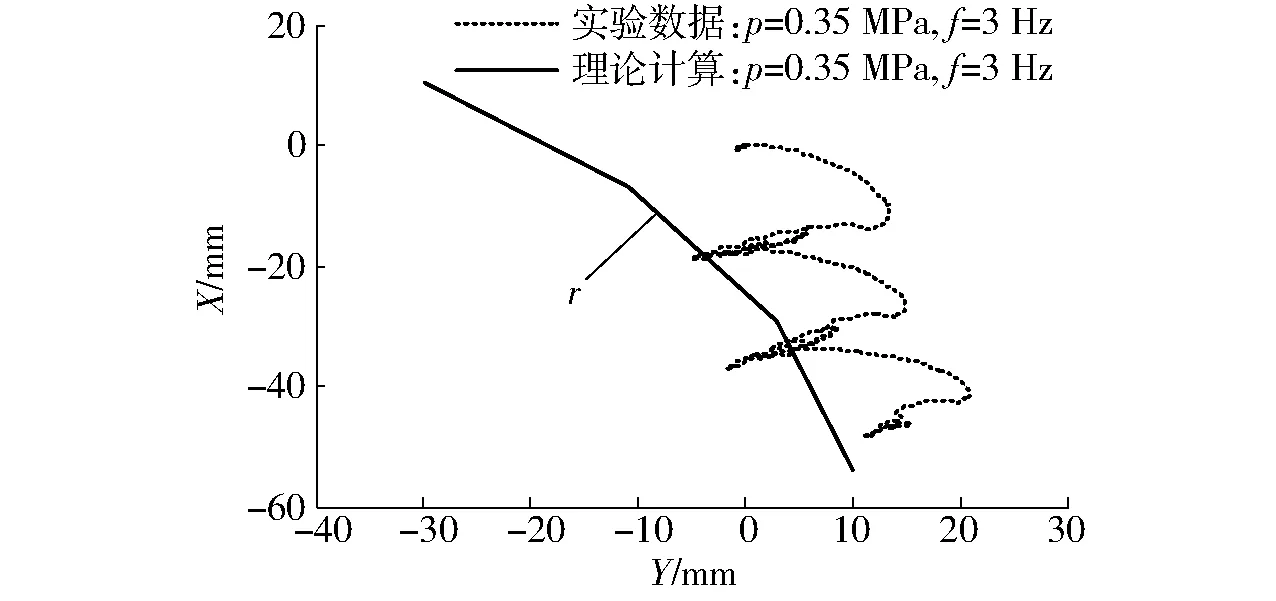
图22 机器人转弯过程中位置变化Fig.22 Changes of position in rotating course of robot

5.2.4机器人运动性能实验

通过运动实验平台进行了不同工作条件下机器人连续行走实验(图23～25)，测试了机器人的运动性能。

(1)气压对机器人前行的影响

图23为负载400 g和步频为5 Hz时，不同气压对机器人前行位移和重心位移影响。由于机器人行进步距随着关节内充入的气压的增加而增大，机器人前进速度随之增加(图23a)；机器人的重心高度随之增加，且机器人重心位移呈有规律周期性波动(图23b)。机器人在0.3、0.4、0.5 MPa时前行z向位移产生的波动量分别为1.30、2.48、4.27 mm。随着气压的增加，重心波动量随之大幅增加，机器人行进稳定性随之变差。关节内气压是影响机器人行进速度和稳定性的关键因素。

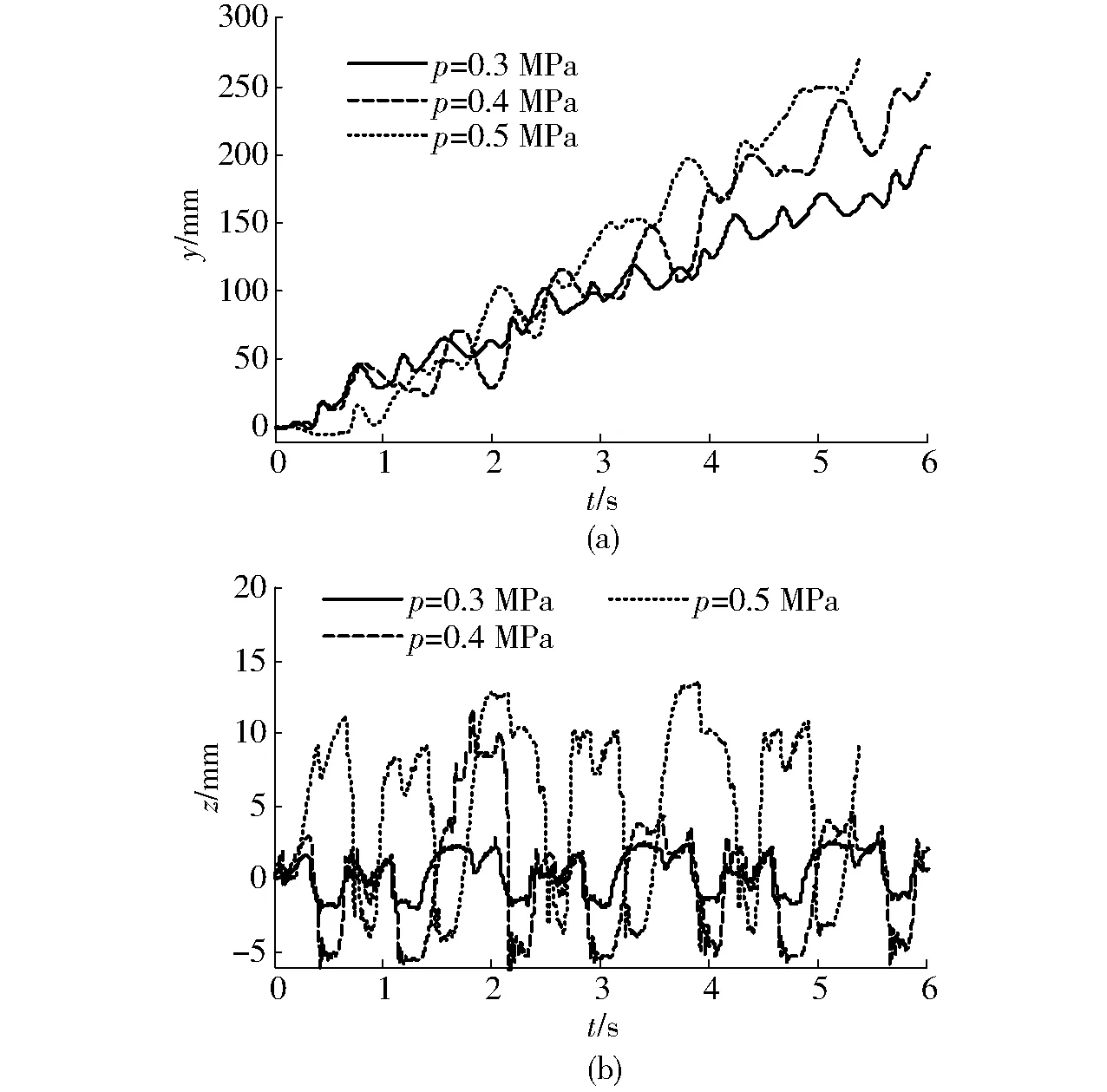
图23 气压对机器人前行的影响Fig.23 Effects of air pressure on stride forward of robot

(2)步频对机器人前行的影响

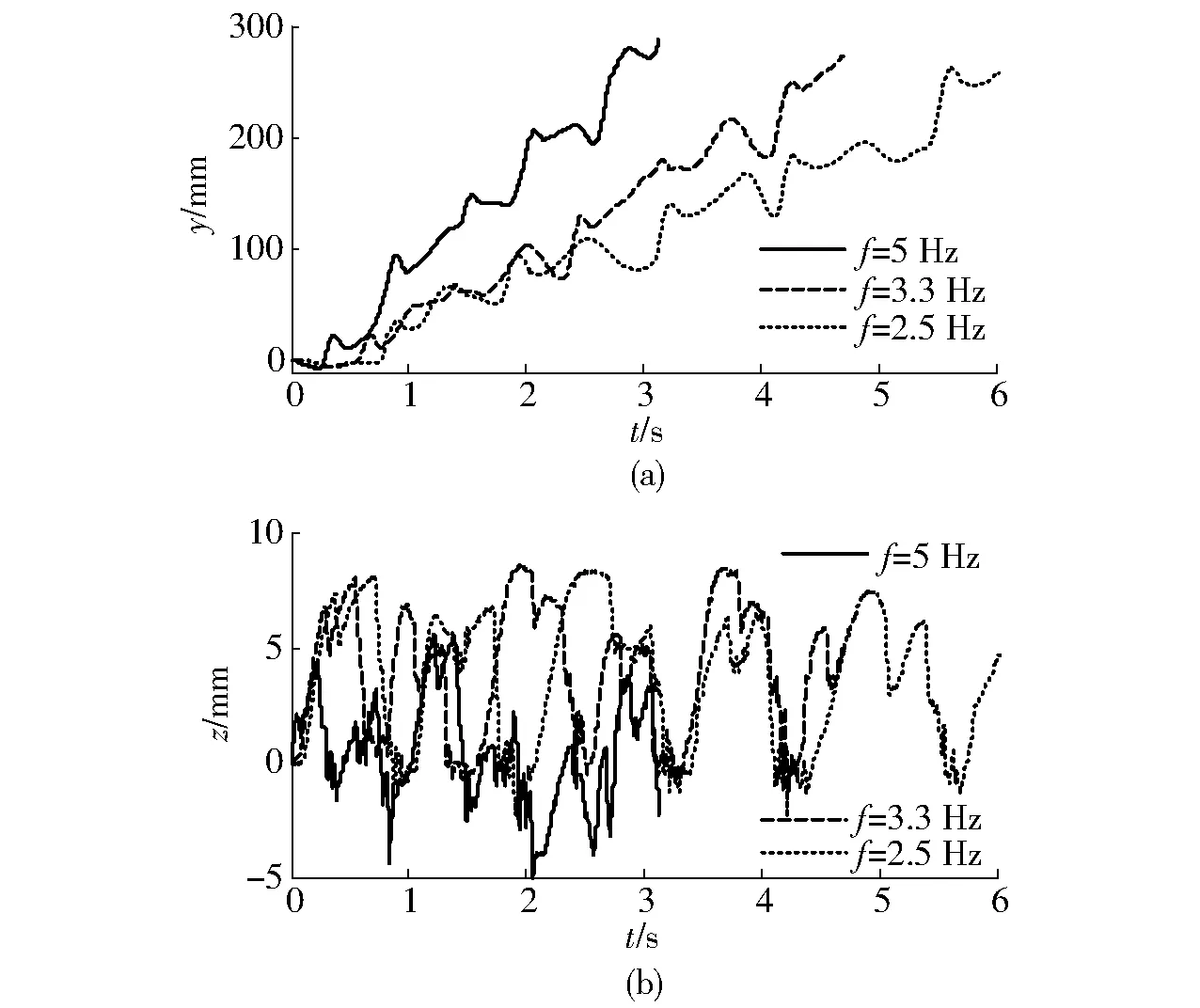
图24 步频对机器人前行的影响Fig.24 Effects of frequency on stride forward of robot

图24为气压为0.4 MPa，负载为400 g时，步频对机器人行进的影响。由图24可看到，随着腿部动作频率的增加，机器人行进速度随之大幅增加(图24a)。在5 Hz下，机器人行进速度可达100 mm/s。

随着步频的增加，机器人重心高度随之下降。机器人在步频为5、3.3、2.5 Hz时前行z向位移产生的波动量分别为2.32、2.84、2.89 mm。其波动量随步频的增加而增加，高频运动时机器人的重心位移波动量较小，行走稳定性较好(图24b)。步频是是影响机器人行进速度和稳定性的重要因素。

(3)负载对机器人前行的影响

图25为气压为0.4 MPa和步频为5 Hz时，不同载荷对机器人前行位移和重心位移影响。机器人前行时，负载对机器人移动速度有一定影响(图25a)。随着载重的增加，六足机器人受到的惯性力随之增加，导致机器人行走时重心明显下降，振动频率随之增大(图25b)。机器人在空载、负载400 g和负载580 g时前行z向位移产生的波动量分别为2.66、2.4、2.55 mm。负载400 g时波动量最小，行走最为稳定。一定负载可增加机器人移动的稳定性。

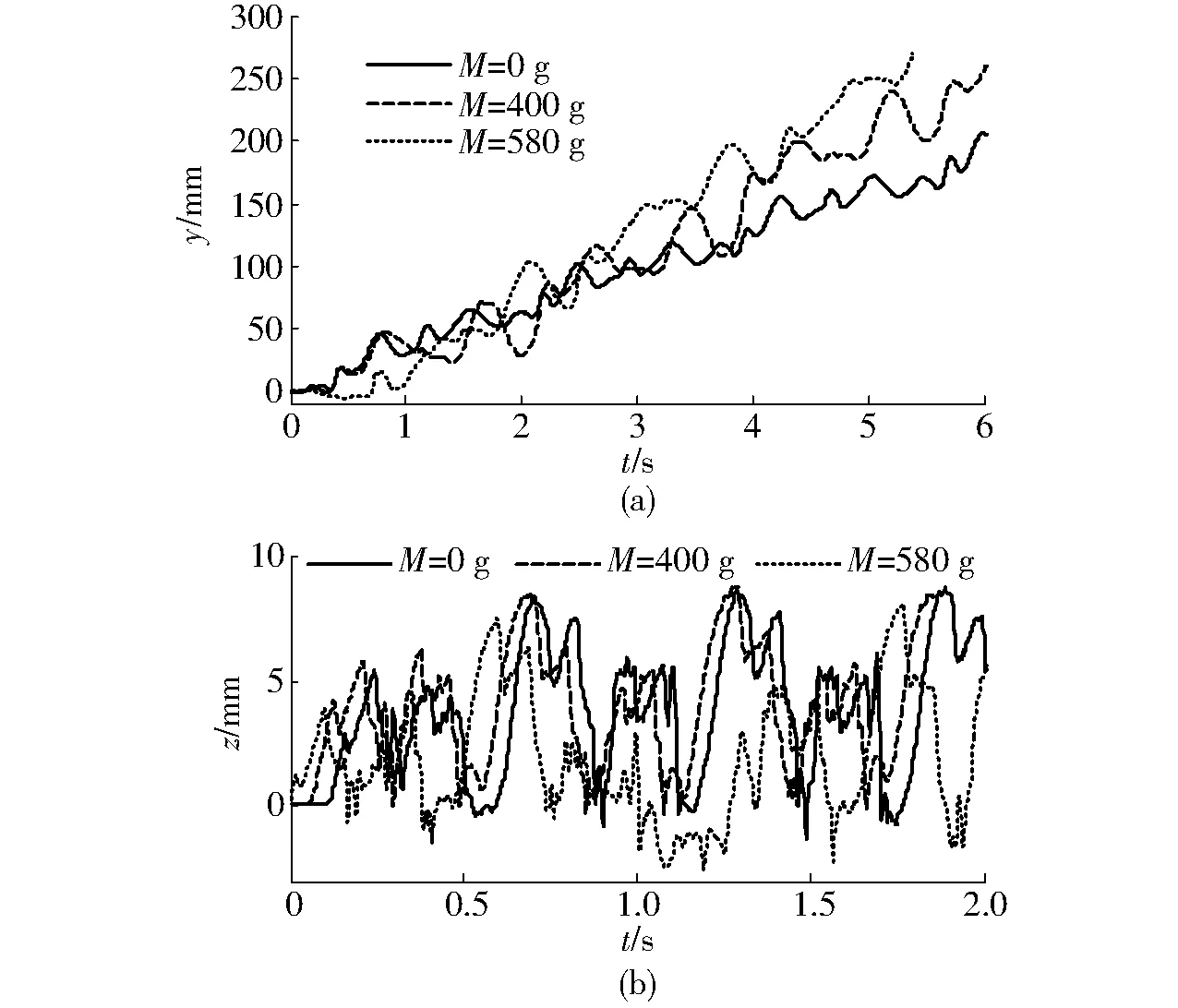
图25 负载对机器人前行的影响Fig.25 Effects of load on stride forward of robot

综上分析，机器人最佳工作条件为工作气压0.3 MPa、步频5 Hz和负载400 g。

6 结论

(1)设计了一种气动柔性关节仿生六足机器人，机器人腿部采用对称分布结构形式，分别位于正六边形的6个顶点上。腿部由气动多向弯曲关节进行驱动，具有多个自由度和较好的灵活性。

(2)通过机器人步态仿真和物理样机实验，验证了步态规划的合理性。前行步态和转弯分别采用“7步法”和“4步法”，在一个循环周期内，机器人可前行4个步距或转过一定角度。

(3)通过对机器人运动学模型和足部工作空间分析表明：足部工作空间呈半球锥形，分布均匀合理，满足机器人腿部的步态要求。机器人步距、移动速度和转角的理论计算与实验数据趋势一致，吻合较好。由于关节弯曲形变量的增加，机器人的步距随着气压的增加而呈非线性增加。通过调整步距可以控制和调节机器人移动速度和转动角度。

(4)机器人运动学实验结果表明：系统内气体压力是影响机器人运动性能的关键因素，随着气压的增加，机器人移动速度随之增加，但稳定性变差。步频是影响机器人移动速度的显著因素，合理负重可增加机器人行进的稳定性。机器人最佳工作条件为工作气压0.3 MPa、步频5 Hz和负载400 g。

1 CHEN Xi, WANG Liquan, YE Xiufen, et al. Prototype development and gait planning of biologically inspired multi-legged crablike robot[J]. Mechatronics,2013, 23:429-444.

2 陈刚,金波,陈鹰.基于速度逆运动学的六足步行机器人位姿闭环控制[J/OL]. 农业机械学报, 2014, 45(5): 265-270.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20140541&journal_id=jcsam.DOI：10.6041/j.issn.1000-1298.2014.05.041.

CHEN Gang, JIN Bo, CHEN Ying. Position-posture closed-loop control of six-legged walking robot based on inverse velocity kinematics [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(5): 265-270. (in Chinese)

3 余联庆,王玉金,王立平,等. 基于机体翻转的四足机器人翻越台阶过程的运动学分析[J]. 中国机械工程, 2012, 23(5): 518-524.

YU Lianqing, WANG Yujin, WANG Liping, et al. Kinematics analysis of quadruped robot climbing step based on body flipping [J]. China Mechanical Engineering, 2012, 23(5):518-524. (in Chinese)

4 宋孟军,张明路. 多足仿生移动机器人并联机构运动学研究[J/OL]. 农业机械学报, 2012, 43(3): 200-206. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20120336&journal_id=jcsam. DOI：10.6041/j.issn.1000-1298.2012.03.036.

SONG Mengjun, ZHANG Minglu. Kinematic analysis for parallel mechanism of bionic-mobile robot [J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(3): 200-206.(in Chinese)

5 尤波,刘宇飞, 高海波, 等.六边形六足机器人障碍自识别步态规划[J]. 哈尔滨理工大学学报, 2013, 18(5): 42-46.

YOU Bo, LIU Yufei, GAO Haibo, et al. Hexagonal hexapod robot obstacle self-identify gait planning[J]. Journal of Harbin University of Science and Technology, 2013, 18(5): 42-46. (in Chinese)

6 陈浩,丁希仑. 四足变结构机器人的运动学分析[J]. 北京科技大学学报, 2012, 34(1): 53-58.

CHEN Hao, DING Xilun. Kinematics analysis of a quadruped robot with variable structure[J]. Journal of University of Science and Technology Beijing, 2012, 34(1): 53-58. (in Chinese)

7 FRED D, MARK E N. Architectures for a biomimetic hexapod robot [J]. Robotics and Autonomous Systems,2000,30:5-15.

8 SHIBENDU S R, DILIP K P. Soft computing-based expert systems to predict energy consumption and stability margin in turning gaits of six-legged robots[J]. Expert Systems with Applications, 2012, 39: 5460-5469.

9 SHIBENDU S R, DILIP K P. Effects of turning gait parameters on energy consumption and stability of a six-legged walking robot[J]. Robotics and Autonomous Systems,2012,60: 72-82.

10 SHIBENDU S R, AJAY K S, DILIP K P. Estimation of optimal feet forces and joint torques for on-line control of six-legged robot[J]. Robotics and Computer-Integrated Manufacturing, 2011, 27: 910-917.

11 SHIBENDU S R, DILIP K P. Dynamic modeling, stability and energy consumption analysis of a realistic six-legged walking robot[J]. Robotics and Computer-Integrated Manufacturing, 2013, 29:400-416.

12 LOC V, ROH S, KOO I M, et al. Sensing and gait planning of quadruped walking and climbing robot for traversing in complex environment [J]. Robotics and Autonomous Systems, 2010, 58:666-675.

13 荣誉,金振林,曲梦可. 三自由度并联机械腿静力学分析与优化[J].农业工程学报,2012,28(20):41-49.

RONG Yu, JIN Zhenlin, QU Mengke. Statics analysis and optimal design of 3-DOF parallel mechanical leg[J]. Transactions of the CSAE, 2012, 28(20): 41-49. (in Chinese)

14 荣誉,金振林,崔冰艳. 六足农业机器人并联腿构型分析与结构参数设计[J].农业工程学报,2012,28(15)：9-14.

RONG Yu, JIN Zhenlin, CUI Bingyan. Configuration analysis and structure parameter design of six-leg agricultural robot with parallel-leg mechanisms[J]. Transactions of the CSAE, 2012, 28(15): 9-14. (in Chinese)

15 WANG Zhiying, DING Xilun, ROVETTA A, et al. Mobility analysis of the typical gait of a radial symmetrical six-legged robot[J]. Mechatronics, 2011, 21:1133-1146.

16 邓宗全,刘逸群,高海波, 等.液压驱动六足机器人步行腿节段长度比例研究[J]. 机器人, 2014, 36(5):544-551.

DENG Zongquan, LIU Yiqun, GAO Haibo, et al. On the segment length ratio of the walking leg of a hydraulically actuated hexapod robot[J]. Robot, 2014, 36(5):544-551. (in Chinese)

17 刘逸群, 邓宗全, 刘振, 等. 液压驱动六足机器人一种低冲击运动规划方法[J]. 机械工程学报, 2015, 51(3):10-17.

LIU Yiqun, DENG Zongquan, LIU Zhen, et al. Low-impact motion planning method of hydraulically actuated hexapod robot[J]. Journal of Mechanical Engineering, 2015, 51(3):10-17. (in Chinese)

18 章永年,王美思,吴阳,等.五连杆足式机器人腿部机构多目标优化算法[J/OL]. 农业机械学报, 2016, 47(10): 398-404.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20161052&flag=1.DOI:10.6041/j.issn.1000-1298.2016.10.052.

ZHANG Yongnian, WANG Meisi, WU Yang, et al. Multi-objective optimization algorithm of robot leg based on planar five-bar mechanism[J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(10): 398-404.(in Chinese)

19 王斌锐，王涛，郭振武，等.气动肌肉四足机器人建模与滑模控制[J]. 机器人, 2017, 39(5):620-626.

WANG Binrui, WANG Tao, GUO Zhenwu, et al. Modeling and sliding mode control of quadruped robot driven by pneumatic muscles[J]. Robot, 2017, 39(5):620-626. (in Chinese)

20 GENG D X, ZHAO J, ZHANG L. Study on bidirectional controllable flexible bending joints based on elongation artificial muscles[J]. Applied Mechanics and Materials, 2011, 44-47: 2883-2887.