区域综合能源系统多主体非完全信息下的双层博弈策略

郝 然, 艾 芊, 姜子卿

(上海交通大学电子信息与电气工程学院, 上海市 200240)

0 引言

随着工业生产和居民用户的能源需求日趋多样,供能设备和形式向着高品位、低成本的方向发展,能源传输与设备的革新促使能源系统间的进一步耦合,使得综合能源系统从理论概念逐渐转变为一种切实有效的能源整合手段。区域综合能源系统(regional integrated energy system, RIES)是能源互联网中常见的载体,涉及能源的转换、分配与协调,其核心是实现多能互济和能源的梯级利用[1-2]。近年来,欧美和日本结合自身能源发展需求,在政策、技术和示范工程方面做了大量尝试[3],国内也针对“互联网+智慧能源”的理念开展了大量的研究和实践[4]。

为实现区域能源网多能互补的系统优化,需采用合作博弈的方法。考虑冷热电多主体多能流的协同,以最优化区域用能能源效率或供能费用为目标,整合系统内多个主体的可调控资源,制定合理的系统级调度计划。而各个主体的利益诉求需要在能源市场非合作竞价博弈中得以体现,进一步降低用户用能成本。

针对RIES多主体、高耦合的内在特性,探索合理的运行机制和多主体市场互动机制是多能互补协同优化的必要条件。在电力系统的研究中,经典博弈论被广泛应用于电力市场竞价策略研究,但其基本假设是每个市场参与者都具有“理性的共同认识”,这种方法存在较大局限性[5-6]。在多主体竞价博弈中,能源市场的相互耦合使得参与主体难以准确掌握全部信息而做出最佳反应动态(best-response dynamic, BRD)[7]。多能市场具有混沌性因而对仿真初值较为敏感,参与主体无法通过构造确定性的动态模型推演系统稳定点。本文基于有限假设理性设计博弈策略,参与者的知识远不能包括全部的博弈结构和规则[8],通过某种传递机制而非纯理性选择策略参与博弈,因此本文的博弈强调策略的动态性和稳定性。

多能协调优化的合作方法一直是多能互补的研究热点,其重点在于分析能量转换与耦合元件特性[9]。多能流静态耦合模型被用于冷热电协同调度和稳态分析中[10-11],研究证明多主体协同互补可降低用能成本、提高能源利用效率[12-13]。为模拟市场中主体的有限理性行为和市场价格形成的动态过程,文献[14-16]将多代理技术应用于电力市场和规划的动态模拟系统中,通过强化学习算法仿真各个主体间的互动博弈行为,研究电力规划和市场定价的决策方法。文献[17]应用多代理技术,对日前电力市场建立动态贝叶斯网络模型,通过贝叶斯学习法仿真发电厂智能体分时段竞价行为。考虑供需双方的动态交互,文献[18]提出一个双边博弈模型,通过市场驱动发电规划和清洁能源的扩容。文献[19-20]运用节点边际定价(locational marginal pricing, LMP)机制,考虑输电网最优潮流和具体的网络拓扑,仿真多个发电厂竞价策略。目前,多数研究集中于输电网发电市场仿真,少有研究涉及RIES能源市场的竞价仿真。

本文以综合能源系统多主体的博弈行为为研究对象。首先,对其关键机组组件的运行特性进行分析,建立基于合作博弈的多能互补下层调度模型并研究上层区域能源市场的竞价演化规律。考虑边际成本报价和按报价结算(pay as bid price,PAB)的收益机制,能源商代理根据下层合作博弈的调度结果,应用强化学习算法分析有限的历史信息,选择不同利润率的报价策略。

1 多主体双层博弈策略

RIES虽与大电网相连,但其生产的电能大部分用于满足内部需求,即某种意义上的直购电,仅有少数电能通过联络线上网,冷热需求也是自给自足的,其内部的能量转化和利用是相对独立的。因此,系统的冷热电价格可由运营部门制定。另外,RIES规模有限,对于机组运行优化的要求较高,不适于采用分时统一价格出清机制,可通过上报包含盈利和边际成本的功率—价格曲线,一方面保证了供能商信息安全,另一方面为园区考虑机组优化调度提供参考依据。

本文设计的多主体双层博弈策略可根据功能划分为调度层和竞价层,如图1所示。调度层的主体为园区独立系统运营商(independent system operator, ISO),接收综合供能商的报价,以单一的系统级经济性为合作优化目标,在可调范围内进行机组边际一致性优化。第二层为竞价层,供能商进行非合作博弈,供能商在不知道对手运行参数的情况下,学习每日不同的利润率报价下的日供能收益并给ISO报价。由此形成调度—竞价双层博弈功能上的循环。

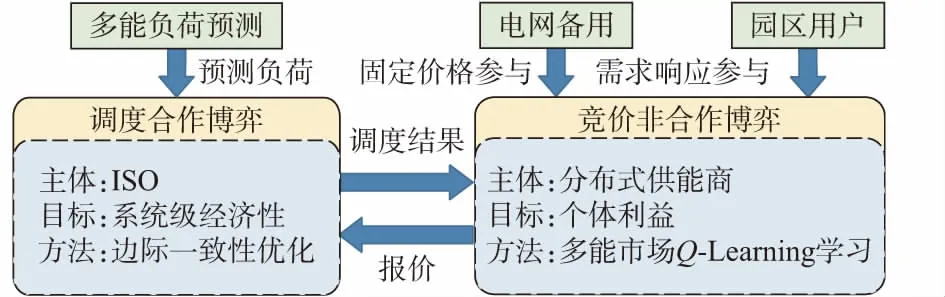
图1 调度-竞价双层博弈策略Fig.1 Dispatch-bidding bi-level game strategy

大型输电网竞价一般是由专家进行分时投标竞价,即每小时出价并由专门的交易平台给出市场出清价格(market clearing price, MCP)。但该方法并不适合规模较小的RIES。因此,本文的竞价方案仅需确定该机组的盈利率,每日上报一次价格。没有基于完全开放的电力市场假设,与电网的联络线功率仍按照分时电价计算,更适用于当今市场环境下的综合能源系统。

整个能源市场中,全部类型的能源供应商,只要处于运行阶段,都可以竞价上网。各供能立体结合区域能源市场信息不完全性,依据自身发电成本通过Q-Learning学习算法自主调整每个周期的竞价策略以获取最大收益。多主体双层博弈的具体策略如图2所示,其中CCHP表示冷热电联供。

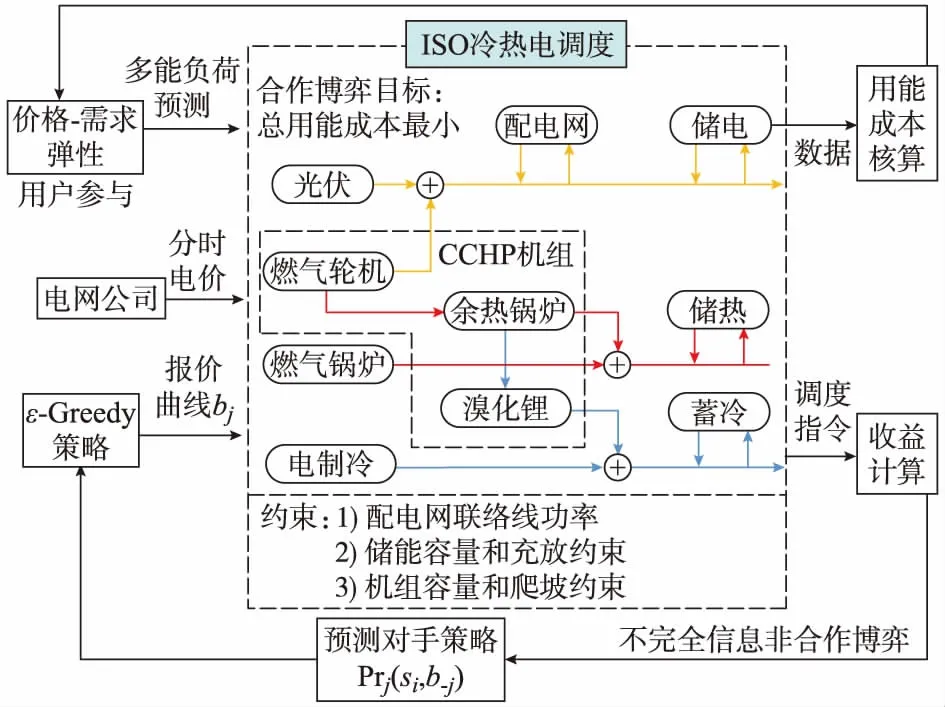
图2 多主体双层博弈策略Fig.2 Multi-agent bi-level game strategy

考虑PAB方式的市场模式,在相同发电报价下,相比系统边际价格(system marginal price,SMP)机制可节省系统购电总成本。在PAB机制下,供能商没有持留容量的利益驱动(假定持留容量前后报价不变),其最优的产量决策是上报最大可用容量,从而可防止供能商在系统容量紧缺时利用持留容量措施操纵市场价格。ISO结合多个主体上报的报价曲线,以系统用能成本最优为目标,充当区域调度中心的撮合者,使不同主体在日前调度上实现合作博弈。为保证公平公正,利益主体在日前调度优化时上报的策略对所有利益主体公开,机组真实的边际成本曲线对外保密。

由于RIES中的传输线路较短,且负荷与供能设备交替布置,故本策略不考虑最优潮流。采用边际定价(marginal pricing,MP)的报价模式简单易行,充分考虑了各台机组的运行特性,实现园区的经济调度,因而可真正地通过多能互补整合各个主体的资源,进而提高能源利用率和新能源利用率。

2 冷热电日前调度合作博弈

2.1 目标函数

ISO调度部门以园区用能费用F最小作为目标函数,协调各个主体合作优化系统目标。目标函数如下:

(1)

供能商成本包括能源转化成本fe,j(t)和运行管理成本fOM,j,边际成本fj(t)可表示为:

fj(t)=fe,j(t)+fOM,j

(2)

(3)

(4)

CCHP机组燃气—发电—发热关系均由标准工况下的实验数据得到,机组实验数据特性如图3(a)所示。

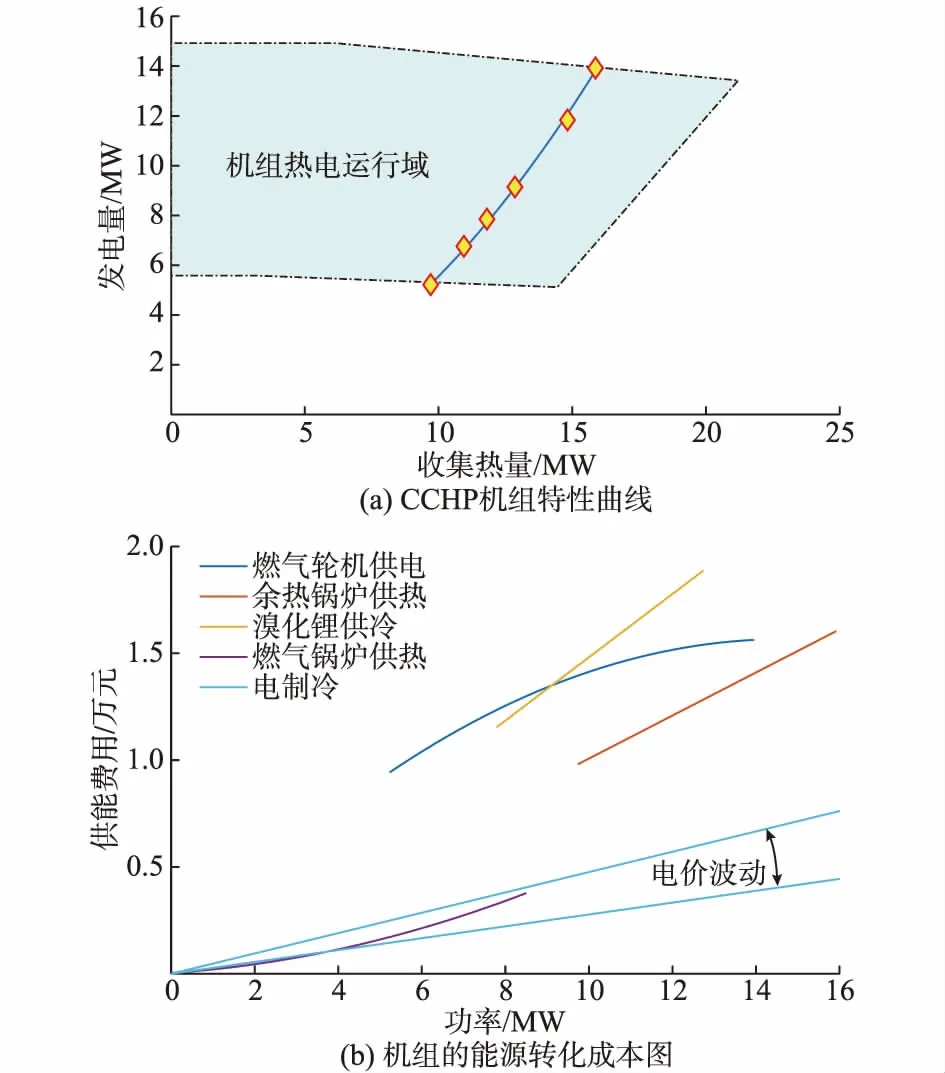
图3 不同机组运行和经济特性图Fig.3 Operation and economic features of different units

余热锅炉发热—燃气量关系由一次函数拟合为H=3.98g,其中H为CCHP机组的热功率,g为天然气消耗量。CCHP机组发电边际成本随燃气的增加而降低,二次函数拟合得到的结果如下:

p=9×10-4g2+0.086g-18.828

2 020 m3/h≤g≤3 980 m3/h

(5)

式中:p为CCHP机组输出的电功率。

根据燃气锅炉的机组特性,其供能费用随运行功率的变化曲线可表示为:

fGB=aGBp2+bGBp+cGB

(6)

溴化锂机组的转换效率η=0.8。电制冷性能系数(COP)值取4,其供能费用随实时电价波动。综上,各个机组的能源转化成本如图3(b)所示,光伏能源转化成本视为0。

2.2 标准工况运行约束

(7)

(8)

(9)

系统约束考虑冷热电功率平衡、区域电网联络线功率PLine约束、冷热电储能充放电约束、冷热电储能爬坡约束及其荷电状态约束,如式(10)所示。溴化锂机组将热功率转化为电功率的效率取为80%。

(10)

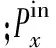
3 非完全信息下的非合作竞价博弈

3.1 用户博弈模型

参考基于用户心理学的分时电价用户需求响应模型[21],设计多种能源消费背景下的用户博弈模型。为保证所有Nash均衡点在合理范围内,用户代表与供能商签订最高出价价格bmax。bref1和bref2为弹性段的投标价格区间。且为防止博弈中出现垄断而出现不合理的价格,用户通过自身的需求响应特性参与博弈,冷热电的用户用能量—价格弹性模型如图4所示。

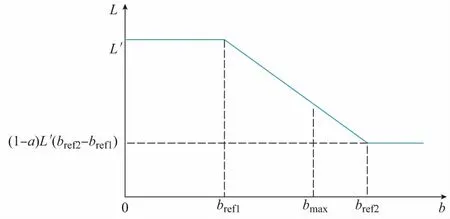
图4 多能流用户用能量-价格弹性模型Fig.4 Elastic model of energy-price for multiple energy users

用电量—电价曲线公式如下:

(11)

3.2 机组边际成本报价机制

为ISO调度提供决策支撑,供能商应根据自身机组运行特性计算边际成本并设计相应的报价策略。为简化分析,本文假定参与主体的报价曲线是成本曲线的比例函数,则引入利润系数kj,设主体j的供能成本曲线为f(t),则报价曲线为bj(t)=kjfj(t),CCHP机组对冷热电独立报价,在计算发电成本时视当前冷热价格和工作状态不变,即发电成本等于总成本减去供冷供热的收益,其他的成本计算同理可得。

实际的RIES包含多个利益主体,在竞价决策时单个主体往往无法获得所有主体的全部成本和容量信息。Q-Learning算法提供智能系统在马尔可夫环境中利用经历的动作序列选择最优动作。其优点在于不需要对所处的动态环境建模,可将多能耦合竞价—调度的复杂过程视为“黑箱”,根据当前信息选择最优动作改变影响动态环境[22-23]。

参考Q-Learning算法[5],设计基于Q-Learning的多能竞价博弈。多代理博弈过程的信息集合为{N,S,R,B,U},其中:N为参与博弈的代理集合;S={si}为博弈的报价的所有离散状态集合,包括各个主体的报价曲线,由下文智能体竞价知识库给出;B={bmin,…,bmax}为主体的报价曲线集合;R={R1,R2,…,Rj,…,Rn}为参与者的收益函数集合,收益函数为参与主体的盈利,具体表达式如式(12)所示。

(12)

参与者的收益函数与博弈状态和参与者的策略有关,即Rj:(si,bj)→R。b-j为竞争对手的报价策略,定义转移概率为在状态S下的状态转移概率U(S,bj,b-j)∈[0,1]。α和γ分别为学习因子和折扣因子。

Q状态更新过程:

Qj(si,bj,b-j)=(1-α)Qj(si,bj,b-j)+

α(Rj(sj,bj,b-j)+γVj(si′))

(13)

Vj定义为在对手采取历史动作b-j,而主体采取可行策略bj∈Br后的最大收益值。

(14)

Prj(si,b-j)是主体对于对手策略的预测。设λj(si,b-j)为对手j在si状态下采取b-j策略的次数。仅基于对手历史数据下的经验给出不同策略的概率:

(15)

Q-Learning算法思想是不去顾及环境模型,直接优化可迭代计算的Q函数,通过评价“状态—行为”对Qj(si,bj,b-j)进行优化,其学习步骤如下。

1)观察当前的状态si和历史报价b-j。

2)选择并且执行一个动作bj。

3)观察下一个状态si′。

4)根据历史数据和收益函数计算立即收益Rj和下一动作后的最大收益V(si′)。

5)更新Q值。

竞价主体仅仅依据Q值大小选取策略,很容易陷入局部最优,一般采用ε-Greedy策略进行优化。策略的突变将导致收益或支付的变化,并不产生新策略,即竞价主体以较大概率选择Q值最大的策略作为最优策略,同时以一个较小概率ε,随机选择除Q值最大以外的其他策略,选择除最优策略以外的其他策略的概率相同。

(16)

概率ε随着过程的收敛而减小,具体表达式为:

(17)

式中:εmax为最大变异概率;m为迭代次数;h为某一保证收敛的迭代次数。

智能体竞价知识库中一共有7种动作,在上一次策略利润率的基础上浮动,最大步长为0.06,具体如下:

(18)

4 算例仿真

仿真中,取学习因子α=0.85,折扣因子γ=0.8,最大变异概率εmax=0.15,h=40。燃气轮机的天然气价格为4.03元/m3,燃气锅炉的气价为3.03元/m3。系统包括2台CCHP机组,1台燃气轮机,最大功率为8 MW的光伏设备和容量为50 MW的电制冷机组。CCHP机组额定功率和ISO运行特性见图3,配备6 MW的溴化锂机组。算例中配电网分时电价为:谷时段(00:00—07:00)为0.514元/(kW·h),峰时段(09:00—23:00)为1.071元/(kW·h),平时段(07:00—09:00,23:00—00:00):0.792元/(kW·h)。

ISO冷热电储能的配置如表1所示,用户需求弹性参数如附录A表A1所示。

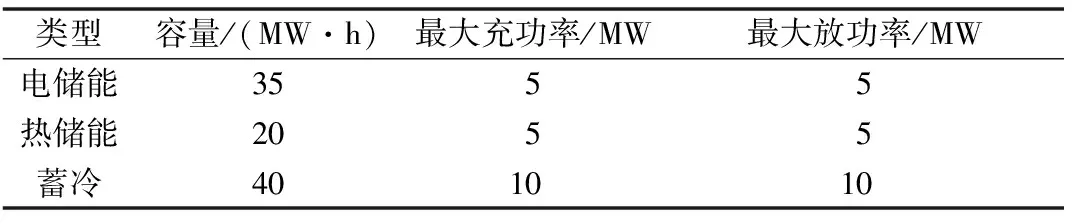
表1 冷热电储能配置Table 1 Configuration of cold, thermal and electric storage

4.1 仿真结果

采用某重点项目园区夏季冷热电典型负荷进行仿真。考虑光伏电站、CCHP能源站、燃气锅炉供暖站和电制冷中央空调4个能源供应商主体进行冷热电竞价仿真,结果如图5所示。

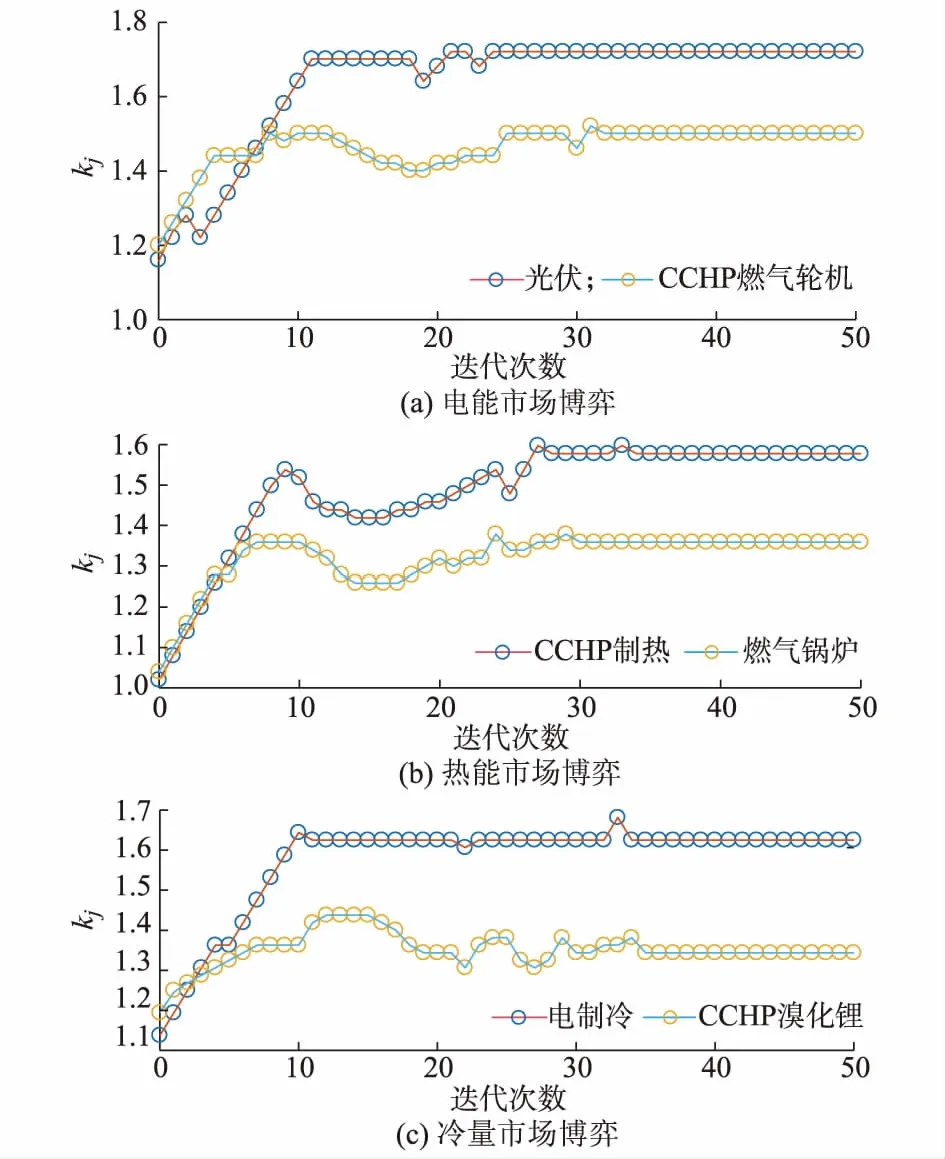
图5 能源市场多主体非完全信息竞价仿真Fig.5 Simulation of multi-agent incomplete information bidding for energy markets

从仿真结果来看,各个供能主体的利润率均从较低水平逐渐增加至均衡点。由于CCHP冷热电以及电制冷的冷电耦合关系,3个竞价过程演化过程类似:均在开始阶段上升较快,供能主体对负荷的竞争关系在第8次到第25次博弈过程中较为明显,在第25次后逐渐平稳。

优化调度在CPLEX平台采用混合整数线性规划实现。由于仅有燃气锅炉和燃气轮机具有二次非线性的函数特征,两台机组非线性成本函数均由ISO情况下实验数据通过构造辅助变量分段线性化表示。在各个主体盈利率均达到均衡点时,冷热电日前合作博弈的调度结果如附录A图A1所示。

由算例分析竞价和调度的耦合机理。ISO根据供能商的报价曲线,本着价格最低的原则制定24 h机组出力,而供能商结合24 h的调度结果计算每个时段的边际价格,计算并预测收益,通过有限理性机器学习模拟人工智能报价并上报,完成层间互动。结合竞价和调度两个过程,分析日前调度结果如下。

1)受限于容量限制,电制冷机组调度功率较大。溴化锂机组受燃气轮机的影响工作在07:00—22:00,蓄冷设备在白天平均电价较高时放冷,在夜间电费较低时吸收冷量。

2)由热能调度结果可知,燃气锅炉在热负荷水平较低时具有价格优势,CCHP机组在热负荷水平较高时具有价格优势。热储能调节机组运行状态,优化机组运行点以降低能量转化费用。

3) 光伏发电时间分布不均,其供能成本低因而基本工作在最大功率点。燃气轮机发电成本随发电功率增加而降低,在负荷较高时燃气轮机运行在额定运行点附近,夜间负荷较低时由配电网和储能供电。

4.2 策略式博弈的局部Nash均衡性证明

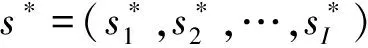
(19)

根据定义验证博弈平衡点的Nash均衡性,假设电价已稳定,设pi为CCHP机组采用si动作的概率,qj为燃气锅炉采用sj动作的概率,选择概率由上文的ε-Greedy算法决定,由贪心策略选择的最大概率为85%,选择其他策略的概率相同,为2.5%。kj的修正步长取最小值0.02。可得两个主体给定点附近的7种策略对应的收益矩阵A7×7和B7×7,其元素aij和bij分别表示两个主体的使用si策略和sj策略时的净收益。

则博弈者1采用策略sj的效用函数为:

(20)

同理可得博弈者2的效用函数为:

(21)

4.3 用户收益对比分析

考虑以下3种模式,对比分析不同策略下的用户收益。

模式1:依据该实际园区的现有固定冷热电价格结算,优化系统经济运行。冷热结算价格分别为0.587元/(kW·h)、0.563元/(kW·h),CCHP上网电价为0.745元/(kW·h),光伏上网电价为0.75元/(kW·h)。

模式2:应用本文提出的调度合作博弈模型,竞价博弈不考虑用户需求响应的参与,通过本文强化学习方法指导竞价行为。

模式3:考虑用户需求响应的参与,应用本文所提的双层博弈调度—竞价策略。

3种模式下分时段总用能成本见附录B表B4,定义平均综合用能成本λ为:

(22)

3种模式平均综合用能成本计算结果见图6。由仿真结果可知,3种模式不同时段的平均用能价格基本有规律:模式1>模式2>模式3。模式3双层博弈后该园区的冷热电的平均收购价格维持在0.524,0.512,0.72元/(kW·h)。相比于该实际园区的现有的固定价格机制,应用相同的调度方法,平均综合购能成本可降低7.19%。

5 结语

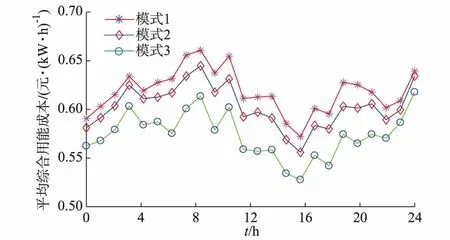
图6 3种模式平均综合用能成本计算Fig.6 Average combined energy cost under 3 modes

本文提出RIES多主体双层博弈策略融合多能互补调度和能源市场竞价过程,以有限的信息和理性为假设基础更接近实际情况。调度部门的合作博弈以系统级优化目标协调各机组和能源,充分发挥了RIES多能互补协调优化的优势。建立了能源市场日前竞价模型,满足供能商的利益诉求并降低能源供应价格。相比单一电力市场仿真,本文提出的策略不仅考虑了调度—竞价两个过程的双层耦合关系,并且将多能耦合模型从调度模型扩展到能量耦合机组的报价策略。由实际算例分析,多主体在本文的竞价机制下均可达到Nash均衡点,ISO在现有报价的基础上制定系统经济最优的调度策略。与现行固定价格结算相比,本文的竞价策略可降低园区7.19%的平均综合用能成本。

然而,本文分析的报价模式是日前统一使用MP策略的报价模式。考虑能源混合潮流的扩展LMP报价策略和结合实际工程数据进行分析将会在后续的研究中展开。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 贾宏杰,王丹,徐宪东,等.区域综合能源系统若干问题研究[J].电力系统自动化,2015,39(7):198-207.DOI:10.7500/AEPS20141009011.

JIA Hongjie, WANG Dan, XU Xiandong, et al. Research on some key problems related to integrated energy systems[J]. Automation of Electric Power Systems, 2015, 39(7): 198-207. DOI: 10.7500/AEPS20141009011.

[2] 吴建中.欧洲综合能源系统发展的驱动与现状[J].电力系统自动化,2016,40(5):1-7.DOI:10.7500/AEPS20150512001.

WU Jianzhong. Drivers and state-of-the-art of integrated energy systems in Europe[J]. Automation of Electric Power Systems, 2016, 40(5): 1-7. DOI: 10.7500/AEPS20150512001.

[3] 余晓丹,徐宪东,陈硕翼,等.综合能源系统与能源互联网简述[J].电工技术学报,2016,31(1):1-13.

YU Xiaodan, XU Xiandong, CHEN Shuoyi, et al. A brief review to integrated energy system and energy internet[J]. Transactions of China Electrotechnical Society, 2016, 31(1): 1-13.

[4] 王伟亮,王丹,贾宏杰,等.能源互联网背景下的典型区域综合能源系统稳态分析研究综述[J].中国电机工程学报,2016,36(12):3292-3305.

WANG Weiliang, WANG Dan, JIA Hongjie, et al. Overview of steady state analysis of typical regional comprehensive energy system under the background of energy internet[J]. Proceedings of the CSEE, 2016, 36(12): 3292-3305.

[5] RASHEDI N, TAJEDDINI M A, KEBRIAEI H. Markov game approach for multi-agent competitive bidding strategies in electricity market[J]. IET Generation Transmission & Distribution, 2016, 10(15): 3756-3763.

[6] 王帅.发电商基于Q-Learning算法的日前市场竞价策略[J].能源技术经济,2010,22(3):34-39.

WANG Shuai. Generators’ bidding strategies in the day-ahead market based onQ-Learning algorithm[J]. Electric Power Technologic Economics, 2010, 22(3): 34-39.

[7] 卢强,陈来军,梅生伟.博弈论在电力系统中典型应用及若干展望[J].中国电机工程学报,2014,34(29):5009-5017.

LU Qiang, CHEN Laijun, MEI Shengwei. Typical applications and prospects of game theory in power system[J]. Proceedings of the CSEE, 2014, 34(29): 5009-5017.

[8] 梅生伟.工程博弈论基础及电力系统应用[M].北京:科学出版社,2016:178-191.

[9] MOGHADDAM I G, SANIEI M, MASHHOUR E. A comprehensive model for self-scheduling an energy hub to supply cooling, heating and electrical demands of a building[J]. Energy, 2016, 94: 157-170.

[10] 周任军,冉晓洪,毛发龙,等.分布式冷热电三联供系统节能协调优化调度[J].电网技术,2012,36(6):8-14.

ZHOU Renjun, RAN Xiaohong, MAO Falong, et al. Coordinated optimization of energy saving for distributed CCHP system[J]. Power System Technology, 2012, 36(6): 8-14.

[11] 顾泽鹏,康重庆,陈新宇,等.考虑热网约束的电热能源集成系统运行优化及其风电消纳效益分析[J].中国电机工程学报,2015,35(14):3596-3604.

GU Zepeng, KANG Chongqing, CHEN Xinyu, et al. Operation optimization of integrated power and heat energy systems and the benefit on wind power accommodation considering heating network constraints[J]. Proceedings of the CSEE, 2015, 35(14): 3596-3604.

[12] GU Wei, WANG Jun, LU Shuai, et al. Optimal operation for integrated energy system considering thermal inertia of district heating network and buildings[J]. Applied Energy, 2017, 199: 234-246.

[13] HERRANDO M, MARKIDES C N, HELLGARDT K. A UK-based assessment of hybrid PV and solar-thermal systems for domestic heating and power: system performance[J]. Applied Energy, 2014, 122: 288-309.

[14] 段炜,胡兆光,吴思竹,等.基于智能体响应均衡模型的经济政策-电力需求动态模拟[J].中国电机工程学报,2014,34(7):1206-1212.

DUAN Wei, HU Zhaoguang, WU Sizhu, et al. Dynamic simulation of economic policy and electricity demand by agents response equilibrium model[J]. Proceedings of the CSEE, 2014, 34(7): 1206-1212.

[15] 田建伟,胡兆光,吴俊勇.基于多智能体建模的经济-电力动态模拟系统[J].中国电机工程学报,2010,30(7):85-91.

TIAN Jianwei, HU Zhaoguang, WU Junyong, et al. Dynamic economy and power simulation system based on multi-agent modeling[J]. Proceedings of the CSEE, 2010, 30(7): 85-91.

[16] 黄仙,郭睿.一种电力市场环境下的电源规划多智能体模型[J].电力系统保护与控制,2016,44(24):1-8.

HUANG Xian, GUO Rui. A multi-agent model of generation expansion planning in electricity market[J]. Power System Protection and Control, 2016, 44(24): 1-8.

[17] DEHGHANPOUR K, NEHRIR M H, SHEPPARD J W. Agent-based modeling in electrical energy markets using dynamic bayesian networks[J]. IEEE Transactions on Power Systems, 2016, 31(6): 4744-4754.

[18] NESHAT N, AMIN-NASERI M R. Cleaner power generation through market-driven generation expansion planning: an agent-based hybrid framework of game theory and Particle Swarm Optimization[J]. Journal of Cleaner Production, 2015, 105: 206-217.

[19] ZHOU Zhi, ZHAO Fei, WANG Jianhui. Agent-based electricity market simulation with demand response from commercial buildings[J]. IEEE Transactions on Smart Grid, 2011, 2(4): 580-588.

[20] TANG W, JAIN R. Dynamic economic dispatch game: the value of storage[J]. IEEE Transactions on Smart Grid, 2016, 7(5): 2350-2358.

[21] 阮文骏,王蓓蓓,李扬,等.峰谷分时电价下的用户响应行为研究[J].电网技术,2012,36(7):86-93.

RUAN Wenjun, WANG Beibei, LI Yang, et al. Study on user response behavior under TOU price[J]. Power System Technology, 2012, 36(7): 86-93.

[22] GAJJAR G R, KHAPARDE S A, NAGARAJU P. Application of actor-critic learning algorithm for optimal bidding problem of a Genco[J]. IEEE Transaction on Power Systems, 2003, 18(1): 11-18.

[23] RAGUPATHI R, DAS T K. A stochastic game approach for modeling wholesale energy bidding in deregulated power markets[J]. IEEE Transactions on Power Systems, 2004, 19(2): 849-856.