考虑条件风险价值的虚拟电厂多电源容量优化配置模型

卫志农, 陈 妤, 黄文进, 胥 峥, 孙国强, 周亦洲

(1. 河海大学能源与电气学院, 江苏省南京市 210098; 2. 国网江苏省电力有限公司盐城供电分公司, 江苏省盐城市 224002)

0 引言

为了有效解决利用可再生能源发电的分布式电源并网后对电网稳定运行带来的威胁[1-3],虚拟电厂(VPP)通过将各类分布式电源、储能系统及可控负荷聚合成一个有机整体参与电力市场的竞标和运营[4],一方面有利于缓解可再生能源对电网造成的波动,另一方面实现了资源的优化利用,从而有望获得规模化的经济效益。

在规划VPP时,要充分考虑分布式电源发电的间歇性、互补性等因素。如何平衡投资与收益,合理配置可再生能源、常规发电机组及储能的容量问题引起了国内外学者关注。文献[5-7]以不同指标表示系统的成本及可靠性,对含有风电、光伏、蓄电池的微网进行容量配置优化,但其仅考虑微网的孤岛运行模式,并没有参与电力市场;文献[8]对VPP中风、光、水、火电进行容量配置,但其仅从自然资源匹配角度考虑容量配置问题,未考虑电价的随机性,也未考虑VPP运行时的各种约束条件。

目前容量配置研究主要集中在微网,而VPP作为一个整体参与市场运营,相对于微网,其在运行方式上可以更加灵活地通过向市场售购电来平抑可再生能源出力的波动。并且,目前对于VPP的研究大多集中在调度运行方面,鲜有文献考虑包括电价随机性在内的VPP规划运行一体化,因此,有必要研究VPP的多电源容量配置问题。

此外,大多数规划问题并没有考虑投资商在收益上面临的不确定性风险[5-8]。投资组合理论可用于权衡资产风险和收益的关系,已在电力建设规划[9]、发电商电量分配[10]以及装机容量优化[11]等领域得到了广泛的应用。不确定因素影响下的多电源容量配置问题也正是投资组合理论中典型的资产配置问题。文献[12]详细地归纳了随机规划模型中常用的风险量度方法,包括利润方差法、风险价值(VaR)法、条件风险价值(CVaR)等。其中CVaR作为一种有效的风险量度手段已经被广泛应用于电力系统的风险管理中[13]。

本文在已有的研究基础上,提出了考虑CVaR的VPP多电源容量优化配置模型,利用CVaR来量度可再生能源出力及市场电价不确定性给规划VPP带来的风险。在规划建设VPP的目标函数中,将CVaR乘上一个权重系数,并以权重系数的大小衡量投资商的风险偏好水平,同时计及VPP实时运行中各种约束条件,建立了考虑CVaR的VPP多电源容量优化配置模型。该模型量化了投资商在规划建设及运行VPP时由于各种不确定因素导致的风险,提供了多电源容量最优配置方案。

1 投资组合理论及基于VaR和CVaR的风险量度方法

1.1 投资组合理论

投资组合问题即投资者如何通过配置各种资产以权衡风险和收益的过程[14]。有效的投资组合必须达到或接近资产收益最大化与风险最小化的均衡状态。在收益一定的条件下,选择风险最小的投资组合，在风险一定的条件下,选择收益最大的投资组合,同时满足这2个条件的投资组合集合就是有效集,又称为有效边界或有效前沿。

在投资建设VPP时,如何选择配置各机组的装机容量以及在运行时段内合理地向市场售购电等均为典型投资组合理论中的资产配置问题[15]。因此,在规划建设VPP时,可应用投资组合理论,合理权衡风险与收益,从而使VPP的配置方案具有更强的鲁棒性。

1.2 基于VaR和CVaR的风险量度

风险量度是指对特定风险发生的可能性或损失的范围与程度进行估计和量度。VaR和CVaR是当前金融领域比较常用的风险管理技术,有效弥补了传统的均值—方差模型在量度风险时的局限性。风险价值的计算方法有历史模拟法和随机模拟法等[16],由于风速、光照强度及电价的概率分布难以准确获得,本文采用历史模拟法来计算风险价值。

VaR反映投资组合在给定的置信度β上潜在的最大损失。设f(x,y)为损失函数,x为决策变量,y为随机变量,假设ρ(y)为y的概率密度函数,则损失函数f(x,y)不大于边界值α的分布函数为:

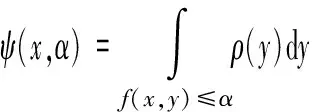
(1)

对于给定的置信度β,VaR可由下式得到:

VVaRβ=min{α∈R:ψ(x,α)≥β}

(2)

然而,VaR只是某个置信度下的分位点,而分位点以后的风险信息未被考虑,即存在“尾部风险”[17]或称为“极端风险”,导致投资组合风险被低估。因此美国学者Rockafell和Uryas于1999年提出了CVaR风险量度方法,其含义为超过VaR部分的平均损失,其作为VaR的一种补充风险量度能够更好地反映“尾部风险”。

(3)

式中:VCVaRβ为置信度β下的CVaR值。

由于VVaRβ(x)解析式难以求出,因此推导出变换函数Fβ(x,α)以求得CVaR:

(4)

式中:[f(x,y)-α]+表示max{f(x,y)-α,0}。

α即为VaR的值。通常用以下估计式来计算变换函数Fβ(x,α):

(5)

式中:y1,y2,…,yq为y的q个样本。

2 VPP多电源容量规划模型

值得注意的是,与常规电源不同,可再生能源的发电量不仅与其装机容量有关,也与环境变量有关,因此为了使VPP投资建设和运行的总成本最小,在规划过程中需要充分考虑常规电源与风、光等可再生能源的协调配合问题。

2.1 VPP典型结构组成与功能

1)光伏发电系统。光伏发电系统的发电功率与光照强度密切相关,假设给定一组光伏电池阵列,其面积和光电转换效率分别为A和η,则这组光伏电池阵列的输出功率为:

Ppv=r1Aη

(6)

式中:r1为这一时间段内的实际光照强度。

以变量Npv表示光伏阵列的并联组数。

2)风力发电系统。一般认为风速服从威布尔分布,可通过下式得到风机的输出功率:

(7)

(8)

式中:Pr为风力发电机的额定功率;vci,vr,vco分别为同型号风力发电机的切入风速、额定风速和切出风速。

以变量Nwind表示风力发电机的台数。

3)柴油发电机。在VPP中通过配置常规机组平抑可再生能源出力的波动性,从而对外输出一个较稳定的电能以参与电力市场运营。以变量Nc表示柴油发电机的台数。

4)储能系统。储能系统不仅起到削峰填谷的作用,还能够根据电力市场价格的波动,灵活地调整VPP在日前市场的电力竞标量。考虑到VPP建设成本的限制,使用寿命较长、功率容量较高的铅酸蓄电池作为储能设备。以变量Nb表示铅酸蓄电池组的并联组数。

5)电力负荷。通常在规划VPP时,需要将对某地区的负荷供应纳入VPP的功能之一。电力负荷又分为固定负荷和可中断负荷,对于可中断负荷,在中断时VPP要向用户支付一定的补偿费用。本文算例负荷为可中断负荷。

2.2 不确定性模拟

本文使用场景集的方法将随机优化问题转化为确定性优化问题处理[18]。分别考虑风电出力、光伏出力及电价场景集w={wi,i=1,2,…,nw},s={sj,j=1,2,…,ns},p={pk,k=1,2,…,np},其中nw,ns,np为相应的场景集个数,各场景概率分别为π(wi),π(sj),π(pk),则总场景数一共为nwnsnp个。以下分析中变量上标wsp均表示该变量在第wi个风电场景、第sj个光伏场景及第pk个电价场景下的形式。

2.3 VPP多电源容量配置问题目标函数

2.3.1系统成本

系统成本包含以下几个方面。

1)等年值初始投资建设成本

Co=(NpvCpv+NwindCwind+NbCb+NcCc)CRF

(9)

(10)

式中:Cpv,Cwind,Cb,Cc分别为单组光伏阵列、单台风机、单组铅酸蓄电池和单台柴油发电机的造价成本;CRF为将初始投资化为等年值的系数因子;m为系统使用年限;r为贴现率。

2)系统年运行维护成本

(11)

3)柴油发电机燃料成本

(12)

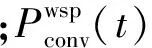
4)柴油发电机环境成本

(13)

式中:ne为考虑的柴油发电机排放污染物总数;m(e),V(e),Y(e)分别为第e项污染物的排放量、环境价值和罚款数量级。

5)可中断负荷补偿成本

(14)

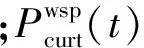
6)VPP运行收益

VPP的运行收益主要来自于在日前市场的收益。

(15)

2.3.2风险量度项

将CVaR以乘以一个风险偏好系数L的形式[19]加入目标函数中。用δ表示CVaR的值:

(16)

2.3.3目标函数

考虑CVaR的VPP多电源容量优化配置模型的目标函数[20]包含两个部分:

(17)

第一部分为等年值总建设运行成本,第二部分为CVaR和一个权重系数的乘积。定义权重系数L为风险偏好系数,表示投资者对于风险的态度,其取值范围为L≥0,当L取较小值时(一般认为L小于0.1为较小)表示投资者为风险偏好型,投资者希望以较大的风险换取较高的收益;当L取较大值时(一般认为L大于0.5为较大),表示投资者为风险规避型,投资策略较保守。投资者应根据自身风险偏好程度,恰当地选取风险偏好系数L。

2.4 约束条件

1)常规机组出力约束

(18)

式中:Pc,max为柴油发电机输出额定功率。

2)蓄电池电量及充放电约束

(19)

(20)

(21)

(22)

3)可中断负荷约束

(23)

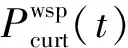
4)功率平衡约束

(24)

5)备用容量约束

(25)

式中:R(t)为t时刻VPP系统所需要的备用容量[21]。

6)CVaR风险约束

(26)

(27)

3 算例求解与分析

3.1 求解方法

本文所建立的优化模型为典型的混合整数线性规划问题,可以在GAMS平台上借助CPLEX求解器进行求解。

3.2 算例参数

选取美国德克萨斯州某地不同区域的风、光资源及电价、负荷数据,采用上述模型进行计算,时间步长取为1 h,计算时间为全年8 760 h。选取过去4年的风、光、电价历史数据作为风、光、电价场景集w,s,p里的不同场景,即nw=ns=np=4,各场景概率均为0.25,对这3个场景集中的4个场景依次进行排列组合,则总场景共有nwnsnp=64个,通过大量场景来模拟VPP中可再生能源出力及电价的不确定性。考虑到负荷数据波动性远小于风速、光照强度及电价数据的波动性,本文忽略负荷数据的波动性,选取过去4年平均历史负荷作为负荷数据。风速[23]、光照[24]、电价[25]及负荷[25]的全年曲线如附录A图A1所示。

考虑到该地区年平均负荷为300 kW,选择额定功率为200 kW的风机;单块最大功率为200 W的光伏电池板,根据系统功率等级要求将14块光伏电池板串联构成一组光伏阵列;采用单体容量为800 Ah的铅酸蓄电池作为储能单元,根据并网电压输入允许范围,将240节电池串联构成一个蓄电池组。本文所选中断补偿费用为40美元/MW,柴油价格取为0.001美元/g。所选风机、光伏电池板、柴油发电机及铅酸蓄电池的具体参数如附录A表A1所示。柴油发电机污染物排放量、环境价值、罚款数量级取自文献[26],具体数据如附录A表A2所示。本文假定所有电源同属于一家投资商。

3.3 算例结果与分析

3.3.1风险系数对容量配置策略的影响

不同风险偏好系数下,VPP的容量配置及目标函数各部分的计算结果如表1所示。可以看出,随着风险偏好系数L的增大,VPP的等年值总建设运行成本λ增加,而CVaR值逐渐减小,说明投资者对风险的厌恶程度加深,规划策略趋于保守。

目前储能技术及价格尚未发展到足以取代常规机组来平抑可再生能源出力的波动,因此当L较小时会优先选择价格较低廉的柴油发电机发电来平抑波动以及大量向市场售电,配置结果中储能数量较少,柴油发电机数量较多;而当L增大时,VPP主要以满足负荷需求及降低电价波动带来的风险性为主,售电量大大降低,风、光配置相应减小。尽管储能及柴油发电机都能够在可再生能源功率缺额时满足负荷需求,但只有储能可以根据电价的波动灵活地通过充放电来调整售电量,显然其风险性相对于柴油发电机更小,因此储能配置比例相对升高。

根据上表结果可以得到总成本关于CVaR的有效前沿曲线[27],如图1所示。

如图1所示可将风险偏好系数水平划分为四部分,分别代表投资商为保守型、较保守型、较激进型和激进型。为了给不同风险偏好的投资商提供容量配置的定量依据,下面分别选取代表4种不同投资策略的风险偏好系数:L=0.05代表投资商为激进型;L=0.1代表投资商为较激进型;L=0.2代表投资商为较保守型;L=2代表投资商为保守型。在此基础上,分别计算4个不同类型投资商规划VPP时的多电源容量最优配置策略,结果如附录A图A2所示。

3.3.2环境成本的敏感度分析

下面对污染物排放的惩罚力度进行敏感度分析,假设投资商确定风险偏好系数为1时,改变环境成本,得到如图2所示配置结果。

当不考虑柴油发电机环境成本时,柴油发电机总装机容量较大,甚至超过可再生能源总装机容量,可以看出此时规划出的VPP仍然是一个以火力发电为主的电厂,其对于分布式能源优化利用效果不明显,污染物排放量较多;当考虑柴油发电机环境成本时,柴油发电机配置比例下降,可再生能源总装机容量大于常规机组,且系统优先使用储能来平抑可再生能源出力波动,此时VPP经济、高效、环保的特点得以体现;当污染物环境价值及罚款数量级提高至5倍时,柴油发电机数量急剧减少,更加充分体现了发展VPP对于环境保护的作用。

图2 环境成本影响下的容量配置比Fig.2 Capacity allocation radio under influence of environmental cost

通过以上敏感度分析可以看出,VPP容量优化配置随国家相关政策的影响较大,为了响应全球节能减排的号召,国家会制定相关政策及相应的补贴,以减少柴油发电机在VPP中的配置比例。

3.3.3自然资源及负荷相关性对容量配置的影响

不同地区自然资源之间或与负荷之间相关性不同,对于VPP容量配置结果也有影响。现选择3个典型场景进行分析:场景1选为w1,s1,p1组成的场景;场景2选为w1,s2,p2组成的场景;场景3选为w4,s3,p1组成的场景。各场景下风险系数均为1,容量配置结果如表2所示。

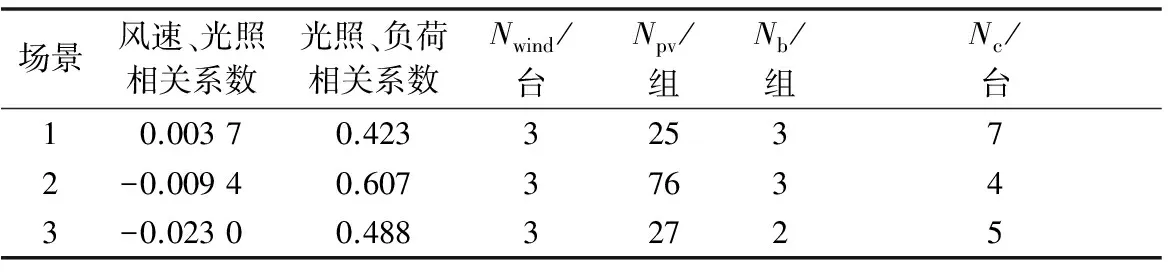
表2 不同场景下容量配置结果Table 2 Capacity allocation results under different scenes

将场景2结果与场景1对比可以看出,当光照、负荷相关程度较高时,此时由于光伏出力波动导致的失负荷的风险减小,因此配置结果中光伏组数较多。将场景3与场景1对比可以看出,当风速、光照呈负相关且程度略大时,说明一定程度上抑制了可再生能源出力总波动,因此配置结果中储能及柴油发电机数量减少,可再生能源配置比例增加。

3.3.4VPP出力计划分析

VPP作为一个电厂,其日前调度出力计划必不可少,当投资商确定风险偏好水平后,本文研究模型不仅能够给出最优的容量配置策略,同时也能够得到VPP每日出力计划。

选取一个典型日24 h (4 560～4 583 h),投资商风险系数选值为1,以此规划出的VPP有3台风机、29组光伏阵列、3组蓄电池串联组及6台柴油发电机。VPP日出力计划如图3所示。

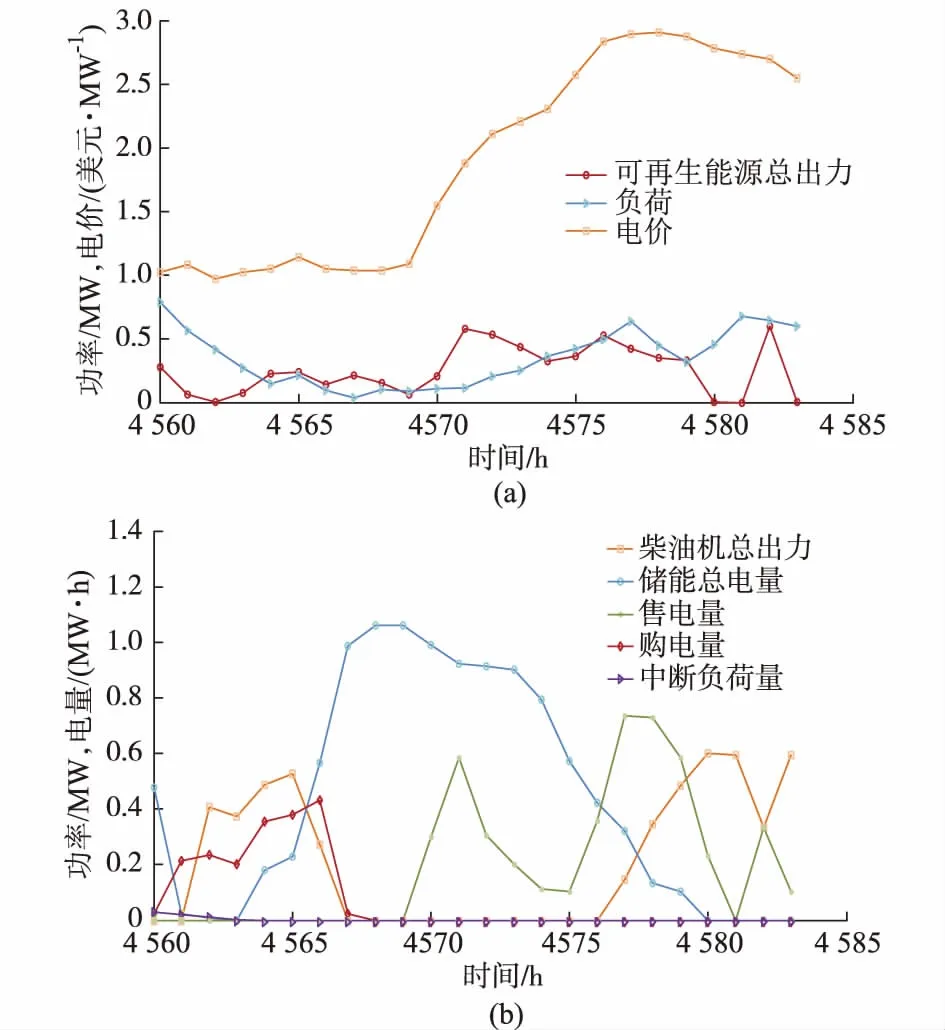
图3 VPP日出力计划Fig.3 Daily output plan of VPP

4 560～4 564 h:电价较低,可再生能源出力小于负荷需求;VPP优先调度储能进行放电,当储能放电量不足以弥补功率缺额时,启动柴油发电机进行发电,由于电价很低,选择购入部分电量及中断部分负荷以满足负荷需求。

4 564～4 569 h:电价较低,可再生能源出力略大于负荷需求;VPP调度可再生能源和柴油发电机剩余出力以及购入部分电量对储能进行充电,当储能电量充满时,停止柴油发电机和购电。不在电价低时向市场售电。

4 569～4 574 h:电价较高,可再生能源出力大于负荷需求;VPP调度可再生能源剩余出力向市场出售,并调度储能适当放电向市场出售。

4 574～4 583 h:电价高,可再生能源出力小于负荷需求;VPP调度储能放电及柴油发电机发电,将满足负荷需求之外的剩余电力全部向市场出售。

4 结论

本文围绕含风、光、柴、储的VPP多电源容量配置问题,建立了基于风险量度理论的VPP投资组合容量规划模型,由研究结果可得结论如下。

1)CVaR的引入能够直观地量度投资者在规划和运行VPP时面临的风险。通过对风险偏好系数的设定能够更好地衡量规划建设VPP的经济性与风险性之间的关系。

2)随着风险偏好系数的增大,配置方案会优先减小波动性大的因素,因此风电的容量配置比下降得最快。

3)在不同风险偏好系数下配置柴油发电机及储能所发挥的功能侧重不同。

4)VPP最优容量配置方案受国家环保政策、选址区域自然资源及负荷相关性等因素影响较大。

此外,本文假设各电源从属于一家投资商,即没有考虑VPP内部既得利益的再分配。因此在本文基础上,可进一步考虑假设在VPP内部利益需要再划分前提下的容量配置问题。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 叶莘,韦钢,马雷鹏,等.含分布式电源的直流配电网供电能力评估[J].电力系统自动化,2017,41(9):58-64.DOI:10.7500/AEPS20161017009.

YE Shen, WEI Gang, MA Leipeng, et al. Power supply capability evaluation of DC distribution network with distributed generators[J]. Automation of Electric Power Systems, 2017, 41(9): 58-64. DOI: 10.7500/AEPS20161017009.

[2] 丁明,王伟胜,王秀丽,等.大规模光伏发电对电力系统影响综述[J].中国电机工程学报,2014,34(1):1-14.

DING Ming, WANG Weisheng, WANG Xiuli, et al. A review on the effect of large-scale PV generation on power systems[J]. Proceedings of the CSEE, 2014, 34(1): 1-14.

[3] 杨丽君,吕雪姣,李丹,等.含分布式电源的配电网多故障抢修与恢复协调优化策略[J].电力系统自动化,2016,40(20):13-19.DOI:10.7500/AEPS20160116002.

YANG Lijun, LYU Xuejiao, LI Dan, et al. Coordinated optimization strategy of multi-fault repair and recovery for distribution network with distributed generators[J]. Automation of Electric Power Systems, 2016, 40(20): 13-19. DOI: 10.7500/AEPS20160116002.

[4] 卫志农,余爽,孙国强,等.虚拟电厂的概念与发展[J].电力系统自动化,2013,37(13):1-9.

WEI Zhinong, YU Shuang, SUN Guoqiang, et al. Concept and development of virtual power plant[J]. Automation of Electric Power Systems, 2013, 37(13): 1-9.

[5] 荆朝霞,胡荣兴,袁灼新,等.含风/光/抽水蓄能并计及负荷响应的海岛微网优化配置[J].电力系统自动化,2017,41(1):65-72.DOI:10.7500/AEPS20160106008.

JING Zhaoxia, HU Rongxing, YUAN Zhuoxin, et al. Capacity configuration optimization for island microgrid with wind/solar/pumped storage considering demand response[J]. Automation of Electric Power Systems, 2017, 41(1): 65-72. DOI: 10.7500/AEPS20160106008.

[6] DUFO-LOPEZ R, BERNAL-AGUSTIN J L, YUSTA-LOYO J M, et al. Multi-objective optimization minimizing cost and life cycle emissions of stand-alone PV-wind-diesel systems with batteries storage[J]. Applied Energy, 2011, 88(11): 4033-4041.

[7] 刘梦璇,王成山,郭力,等.基于多目标的独立微电网优化设计方法[J].电力系统自动化,2012,36(17):34-39.

LIU Mengxuan, WANG Chengshan, GUO Li, et al. An optimal design method of multi-objective based island microgrid[J]. Automation of Electric Power Systems, 2012, 36(17): 34-39.

[8] 黄昕颖,黎建,杨莉,等.基于投资组合的虚拟电厂多电源容量配置[J].电力系统自动化,2015,39(19):75-81.DOI:10.7500/AEPS20141110001.

HUANG Xinying, LI Jian, YANG Li, et al. Investment portfolio based multi energy capacity allocation of virtual power plant[J]. Automation of Electric Power Systems, 2015, 39(19): 75-81. DOI: 10.7500/AEPS20141110001.

[9] ELAINE K, HART M, JACOBSON Z. A Monte Carlo approach to generator portfolio planning and carbon emissions assessments of systems with large penetrations of variable renewable[J]. Renewable Energy, 2011, 36(8): 2278-2286.

[10] 苗福丰,唐西胜,齐智平.储能参与风电场惯性响应的容量配置方法[J].电力系统自动化,2015,39(20):6-11.DOI:10.7500/AEPS20150201006.

MIAO Fufeng, TANG Xisheng, QI Zhiping. Capacity configuration method for wind power plant inertia response considering energy storage[J]. Automation of Electric Power Systems, 2015, 39(20): 6-11. DOI: 10.7500/AEPS20150201006.

[11] 郑雅楠,周明,李庚银.大用户购电组合决策模型及对比分析[J].电网技术,2011,35(3):188-194.

ZHENG Yanan, ZHOU Ming, LI Gengyin. Decision-making models for large consumer electricity purchasing portfolio and contrastive analysis on them[J]. Power System Technology, 2011, 35(3): 188-194.

[12] ZHENG Q P, WANG J H, LIU A L. Stochastic optimization for unit commitment: a review[J]. IEEE Transactions on Power Systems, 2015, 30(4): 1913-1924.

[13] ROCKAFELLAR R T, URYASEV S. Optimization of conditional value-at-risk[J]. Journal of Risk, 2000, 2(3): 21-41.

[14] 徐维军,周平平,李婷,等.基于CVaR和多元权值约束下的积极投资组合模型[J].系统管理学报,2017,26(2):219-224.

XU Weijun, ZHOU Pingping, LI Ting, et al. Active portfolio model with CVaR and multiple weight constraints[J]. Journal of Systems & Management, 2017, 26(2): 219-224.

[15] 张江林,夏榆杭,段登伟,等.基于WCVaR评估的虚拟发电厂能量市场收益-风险模型[J].电力系统自动化,2017,41(9):77-83.DOI:10.7500/AEPS20160716004.

ZHANG Jianglin, XIA Yuhang, DUAN Dengwei, et al. Benefit-risk model of virtual power plant in energy market based on WCVaR assessment[J]. Automation of Electric Power Systems, 2017, 41(9): 77-83. DOI: 10.7500/AEPS20160716004.

[16] URYASEV S. Conditional value at risk, optimization algorithms and applications[J]. Financial Engineering News, 2000, 2(3): 1-5.

[17] 黄友珀,唐振鹏,周熙雯.基于偏t分布realized GARCH模型的尾部风险估计[J].系统工程理论与实践,2015,35(9):2200-2208.

HUANG Youpo, TANG Zhenpeng, ZHOU Xiwen. Estimation of tail risk based on realized GARCH model with skew-tdistribution[J]. Systems Engineering—Theory & Practice, 2015, 35(9): 2200-2208.

[18] RAMLI M A M, HIENDRO A, AL-TURKI Y A. Techno-economic energy analysis of wind/solar hybrid system: case study for western coastal area of Saudi Arabia[J]. Renewable Energy, 2016, 91: 374-385.

[19] 王海冰,王承民,张庚午,等.考虑条件风险价值的两阶段发电调度随机规划模型和方法[J].中国电机工程学报,2016,36(24):6838-6848.

WANG Haibing, WANG Chengmin, ZHANG Gengwu, et al. Two-stage stochastic generation dispatching model and method considering conditional value-at-risk[J]. Proceedings of the CSEE, 2016, 36(24): 6838-6848.

[20] DABBAGH S R, SHEIKH-EL-ESLAMI M K. Risk assessment of virtual power plants offering in energy and reserve markets[J]. IEEE Transactions on Power Systems, 2016, 31(5): 3572-3582.

[21] SHABANZADEH M, SHEIKH-EL-ESLAMI M K, HAGHIFAM M R. The design of a risk-hedging tool for virtual power plants via robust optimization approach[J]. Applied Energy, 2005, 155: 766-777.

[22] ARDAKANI F J, RIAHY G, ABEDI M. Optimal sizing of a grid-connected hybrid system for north-west of Iran-case study[C]// IEEE Environment and Electrical Engineering, May 16-19, 2010, Prague, Czech Republic: 1369-1380.

[23] NREL [EB/OL]. [2015-10-24]. http://wind.nrel.gov/Web_nrel/.

[24] NREL [EB/OL]. [2015-10-24]. http://www.nrel.gov/electricity/transmission/solar_integration_methodolog.html.

[25] PJM [EB/OL]. [2017-01-21]. http://www.pjm.com/markets-and-operations/ancillary-services.aspx.

[26] 钱科军,袁越,石晓丹,等.分布式发电的环境效益分析[J].中国电机工程学报,2008,28(29):11-15.

QIAN Kejun, YUAN Yue, SHI Xiaodan, et al. Environmental benefits analysis of distributed generation[J]. Proceedings of the CSEE, 2008, 28(29): 11-15.

[27] 刘小茂,李楚霖,王建华.风险资产组合的均值-CVaR有效前沿(Ⅱ)[J].管理工程学报,2005,19(1):1-5.

LIU Xiaomao, LI Chulin, WANG Jianhua. Mean-CVaR efficient frontier and its economic implications (Ⅱ)[J]. Journal of Industrial Engineering and Engineering Management, 2005, 19(1): 1-5.