面向多能互补的分布式光伏与气电混合容量规划方法

马溪原, 郭晓斌, 雷金勇

(南方电网科学研究院有限责任公司, 广东省广州市 510080)

0 引言

多能互补分布式能源综合利用是清洁能源与可再生能源高效利用的重要方式[1-3]。在众多的多能互补系统形态中,含分布式光伏发电(PV)和“气电混合(P2G)”的区域多能互补分布式能源配电系统是一种典型形式。本文中的“气电混合”指的是通过电能与燃气之间的能量转化和互联实现配电网与天然气网络的协同运行[4-6]。对含分布式光伏与气电混合的区域多能互补系统在容量上进行合理规划,可以在兼顾系统经济性的基础上提高对分布式光伏的消纳能力。

目前对分布式光伏发电规划的研究主要从配电网接纳能力的角度出发,重点关注配电网内部的电压不越限与功率平衡等电网安全性要求。文献[7-9]考虑了电压不越限时分布式光伏所能允许接入的容量极限;文献[10]提出了考虑潮流倒送约束的分布式光伏的选址、定容和规划方法,在气电混合容量规划方面,主要考虑天然气网络规划与电网规划的协调互补问题;文献[11-14]重点考虑了天然气网络约束的气电互联系统协调扩容的规划方法;文献[15]建立了重点考虑电网和气网经济性的长期多区域、多阶段的规划模型。但是,在分布式光伏与气电混合联合运行系统的规划方面,目前研究仍然较少。

多能互补系统中分布式光伏与气电混合容量规划主要存在以下问题。

1)现有的研究对分布式光伏出力的间歇性和负荷用电随机性考虑不够,多在确定性的典型日或确定性的负荷峰值情况下进行分析,缺少基于概率性分析的运行成本期望计算,得到的优化结果往往仅能适应某些典型日场景,不能体现分布式光伏发电和负荷的季节性差异、日差异和中长期特性。

2)规划往往相对割裂,多数仅针对分布式光伏发电系统或仅针对气电混合系统分别开展,在多能互补的环境下,为了有效提高系统经济性,应更好地利用不同能源的时空互补性,建立分布式光伏与气电混合容量的协同优化模型。

3)规划阶段往往缺少对实际运行策略的考虑,容易导致规划结果与实际运行脱节。

针对以上问题,本文的创新性工作主要体现在以下几个方面。

1)考虑到光照强度、负荷均具有显著的时序性和季节性,提出了采用光照强度与负荷的季节性日场景削减结果作为规划模型输入的思想,建立了多场景随机规划模型。

2)提出了多能互补系统中分布式光伏与气电混合的协同规划方法,建立了协同规划模型的目标函数和约束条件。

3)在由分布式光伏与气电混合组成的多能互补系统规划问题中考虑系统运行的影响,以多场景下的多能互补系统的基础投资成本和运营成本综合最低为优化目标,将季节性多个不同场景下的运行成本与收益进行加权计算。

1 分布式光伏与气电混合区域多能互补配电系统典型结构

含分布式光伏发电与气电混合的区域多能互补配电系统位于能源消费末端,主要由分布式光伏发电系统、气电混合装置(电转氢气或甲烷)、氢储能装置、配电网、燃气网和控制系统等部分组成。其典型结构如图1所示。

图1 含分布式光伏发电与气电混合的多能互补配电系统的典型结构Fig.1 Typical structure of multi-energy coupled distribution system with distributed PV and P2G

分布式光伏发电系统在用户侧实现“自发自用,余量上网”。当分布式光伏发电盈余较大导致配电网无法消纳时,一方面,电转甲烷装置启动,把多余的分布式光伏发电量转换成甲烷并注入天然气网络;另一方面,电转氢气装置也可以启动,把多余的分布式光伏发电量转换成氢能的形式存储在氢储能装置中。当上级电网供电能力不足或分布式光伏发电量较小时,氢燃料电池将氢储能中的氢能转化成电能送入电网。气电混合在区域多能互补配电系统中的作用主要是解决分布式光伏高渗透率地接入配电网后的消纳问题。

自然资源、负荷水平、市场价格和运行策略等均对多能互补配电系统中分布式光伏与气电混合容量规划结果有重要影响。本文通过建立含分布式光伏与气电混合的多能互补配电系统稳态模型,计及“市场价格”和“运行策略”的影响,测算多能互补配电系统的运营成本;通过光照强度与负荷季节性多场景,刻画多能互补配电系统所在地的“自然资源”和“负荷水平”。

2 光照强度与负荷的季节性日场景

分布式光伏发电与负荷均具有日规律性和季节性。考虑到本文研究的对象为规划问题,在规划阶段需要更加关注分布式光伏发电及负荷的中长期特性和互补效应,本文提出采用从光照强度历史曲线和负荷历史曲线中按照不同季节提取典型日曲线作为规划模型的输入数据的思想,以此为基础构建随机规划模型。

在该规划模型中,光照强度和负荷需求是两个相互独立的随机变量,如果在规划模型中利用全部的光照强度和负荷需求的历史数据信息进行仿真、计算和分析或进行大量的长周期的随机生产模拟,求解运算量庞大且耗时较长。针对以上问题,本文按照不同季节将光照强度日曲线和负荷日曲线划分成春季、夏季、秋季和冬季共4个样本集,运用“场景削减”的思想将海量样本集缩减为少量的离散样本,在减少计算量的同时计及分布式光伏发电出力与负荷的随机性、时序特性和季节规律。本文采用同步回代消除法[16]进行场景削减,该算法每次迭代削减一个场景并改变其他场景的概率,直到剩余场景集数量达到指定的阈值。

3 分布式光伏与气电混合容量规划的多场景优化模型

本文建立了面向多能互补配电系统的分布式光伏与气电混合容量规划问题的数学优化模型,下面就该数学优化模型的目标函数和约束条件进行详细介绍。

3.1 目标函数

本模型以系统初始投资、维护和运营的综合成本最低为优化目标。其中,运营成本与光照强度和负荷需求有关,具有一定的随机性,同时也受系统运营方式和控制策略影响。目标函数为:

(1)

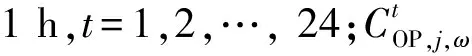
3.1.1等年值设备投资成本CCP,i

第i个设备的等年值设备投资成本如下:

(2)

式中:r为贴现率[17],本文取6.7%;βi为第i个一次设备的单位容量价格;PCapacity,i为第i个设备的容量;ri为第i个设备的设计、安装、调试和配套二次设备投资等费用占一次设备成本的比例,本文取12%;Yi为第i个设备的财务周期,本文取20 a。

3.1.2设备年维护成本CM,i

设备的年维护成本与设备类型、容量规模,需要运行维护人员的数量,每年定期进行大修、巡检的次数,零配件故障率及更换价格有关。本文采用简化的计算公式如下:

CM,i=kM,iPCapacity,i

(3)

式中:kM,i为第i个设备单位容量的年维护成本系数。

本文在计算综合运营成本时不站在特定利益相关方的立场考虑其一方的成本,而是从多种能源在多能互补配电系统中的生产、传输、存储和消费的全过程成本和效率角度出发,实现能源全社会综合利用成本最低。

(4)

式中:N为配电网负荷节点集合,n∈N;各种成本和收益项的计算方法如下。

在第j个季节的某个场景下,第t个时段配电网中第n个节点的用电成本计算公式为:

(5)

在第j个季节的某个场景下,第t个时段配电网的网损等价成本计算公式为:

(6)

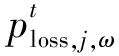
从本文所述系统运行策略可见,因为电转甲烷装置启动的条件是配电网无法就地消纳盈余的分布式光伏发电,电转甲烷装置输入的电量实质上来自于分布式光伏发电,所以该装置输入电量的单位成本为光伏上网电价。由上述分析可见,在第j个季节的某个场景下,第t个时段的电转甲烷装置运营成本计算公式为:

(7)

同上述电转甲烷装置类似,电转氢气装置输入电量来自于系统过剩的分布式光伏发电,输入电量的单位成本为光伏上网电价。在第j个季节的某个场景下,第t个时段的电转氢气装置的运营成本计算公式为:

(8)

在第j个季节的某个场景下,第t个时段的氢燃料电池的运营成本计算公式为:

(9)

在第j个季节的某个场景下,第t个时段分布式光伏发电的运营收益计算公式为:

(10)

3.2 约束条件

3.2.1配电网运行约束

1)有功平衡约束。对于任何季节下任何光照强度和负荷场景,配电网满足有功平衡约束(发电=用电),即

∀j∈J,∀ω∈SPV,j∪SL,j,∀t∈T

(11)

2)节点电压约束。对于任何季节下任何光照强度和负荷场景,配电网中各节点n的运行电压水平应限制在极限范围内,即

∀j∈J,∀ω∈SPV,j∪SL,j,∀t∈T,∀n∈N

(12)

式中:Un,min和Un,max分别表示节点n的最小允许电压值和最大允许电压值,分别取0.93(标幺值)和1.07(标幺值)。

3)支路输电能力约束。对于任何季节下任何光照强度和负荷场景,配电网中各支路l的电流应限制在其所允许的最大电流值内,即

∀j∈J,∀ω∈SPV,j∪SL,j,∀t∈T,∀l∈L

(13)

3.2.2燃气网运行约束

1)燃气网管道流量约束

对于任何季节下任何光照强度和负荷场景,天然气管网流量受管道的最大流量约束,即

∀j∈J,∀ω∈SPV,j∪SL,j,∀t∈T

(14)

2)燃气网节点流量平衡约束

对于任何季节下任何光照强度和负荷场景,燃气网中的每一个节点gn有类似于电网基尔霍夫电流定律的流量平衡条件,即节点进气流量等于出气流量。

∀j∈J,∀ω∈SPV,j∪SL,j,∀t∈T

(15)

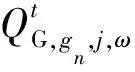
3.2.3分布式光伏出力约束

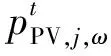
∀j∈J,∀ω∈SPV,j∪SL,j,∀t∈T

(16)

∀j∈J,∀ω∈SPV,j∪SL,j,∀t∈T

(17)

式中:Irc为当前工作点的辐照度;β为功率温度系数;Tc为工作点的电池表面温度,本文在此近似取为环境温度;TSTC为标准额定条件温度,本文取25 ℃;Ir,STC为标准额定条件下的光伏发电功率,本文取Ir,STC=1 kW/m2。

3.2.4电转甲烷装置能量转化约束

∀j∈J,∀ω∈SPV,j∪SL,j,∀t∈T

(18)

∀j∈J,∀ω∈SPV,j∪SL,j,∀t∈T

(19)

3.2.5电转氢气-氢储能-氢燃料电池联合系统能量转化约束

电转氢气装置、氢储能装置和氢燃料电池三者共同组成一个联合系统。当配电网中分布式光伏发电盈余较大时,由电转氢气装置将电能转化为氢能并存储在氢储能装置中;当分布式光伏发电盈余较小时,氢储能装置中的氢输送到氢燃料电池中发电,存储的氢能通过电能的形式反送到配电网中。3个装置联合运行时,尽管存在多次的能量形式转换,为了便于分析和建模,本文均用电能或等效电能的形式刻画能量流。

∀j∈J,∀ω∈SPV,j∪SL,j,∀t∈T

(20)

式中:ηele-P2H为电转氢气装置的能量转换效率,本文取80%。

∀j∈J,∀ω∈SPV,j∪SL,j,∀t∈T

(21)

∀j∈J,∀ω∈SPV,j∪SL,j,∀t∈T

(22)

∀j∈J,∀ω∈SPV,j∪SL,j,∀t∈T

(23)

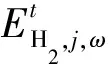
∀j∈J,∀ω∈SPV,j∪SL,j,∀t∈T

(24)

式中:ηFC为氢燃料电池的综合转换效率,本文取55%。

∀j∈J,∀ω∈SPV,j∪SL,j,∀t∈T

(25)

4 问题求解

4.1 系统运行策略

由前所述,多能互补配电系统的运营成本受系统运行策略的影响很大,需要考虑通过分布式光伏和气电混合装置的协调运行,在满足各种配电网运行约束、燃气网运行约束以及各种机组约束的基础上,为实现光伏的高渗透率接入和能源综合利用效率的提高。本文设计了一种典型的多能互补配电系统的能量管理策略,其基本原则如下。

1)优先利用分布式光伏发电为负荷供电,光伏可以反送配电网。

2)若分布式光伏反送配电网使配电网母线电压超过上限或线路传输功率超过上限时,为了消除这些配电网运行越限情况并尽量避免“弃光”,优先启动电转氢气装置,并把多余的分布式光伏发电量存储在氢储能装置中。当电转氢气装置的输出达到上限时,启动电转甲烷装置,把部分多余的分布式光伏发电量转换成甲烷注入天然气网络(此处考虑到“电转甲烷”的损耗和成本比“电转氢气存储后再发电”大,故而优先启用后者)。

3)当电转甲烷过程导致天然气网络的管道流量越限时,降低电转甲烷装置功率;当电转氢气过程导致氢储能装置储气量达到上限时,停止电转氢气装置。

4)当分布式光伏发电未导致配电网母线电压或线路功率越限触发电转甲烷和电转氢气装置启动时,启动氢燃料电池发电,将氢储能中存储的氢气转化成电能反送回配电网,即通过“分布式光伏发电→(电转氢气)氢气→氢储能→(燃料电池)电能”的能源存储和转换的循环过程,充分利用配电网难以消纳的分布式光伏发电电量,尽量避免“弃光”。

5)当依次考虑电转氢气和电转甲烷消纳分布式光伏发电盈余电量仍不能满足母线电压超过上限或线路传输功率超过上限时,出于系统安全运行的考虑,降低分布式光伏出力。

综上所述,为计算运营成本而开展的运行模拟流程见附录A图A1。

4.2 求解算法

由于上述容量规划模型中,在测算运营成本时需要启用配电网潮流计算(本文采用前推回代法),同时附录A图A1中系统运行策略存在诸多逻辑判断,是一个典型的多元非线性最优化问题,无法直接采用线性规划法、混合整数线性规划法和拉格朗日松弛迭代法等理论较为成熟的数学算法寻求最优解。考虑到细菌觅食算法(bacterial foraging algorithm,BFA)在求解含有低维度变量的连续优化问题上易跳出局部极小值,具有很强的全局搜索和精细搜索能力等优点[20-21],并且本文中研究的光伏发电和电转气容量规划模型中的决策变量较少,也属于低维度连续优化问题,因此选择BFA作为求解该容量规划模型的人工智能算法。关于BFA的具体介绍见文献[20],本文不再赘述。

采用BFA的分布式光伏与气电混合容量规划流程如图2所示。

图2 采用BFA算法的分布式光伏与气电混合容量规划流程Fig.2 Flow chart of optimal capacity planning for distributed PV and P2G using BFA

BFA中的适应值取式(1),其计算方法由第3节的目标函数、约束条件和系统运行策略共同决定。细菌空间矢量θ=[θ1,θ2,…,θS]T由各设备的容量PCapacity,i组成,即本文优化模型中的决策变量(分布式光伏发电、电转氢气装置、电转甲烷装置、氢储能装置和氢燃料电池的装机容量)。

5 算例分析

典型算例如图1所示,共有10个节点和8条支路,节点1至7为配电网节点,节点8至10为燃气网节点且无气负荷;配电网电压等级为10 kV,通过110 kV/10 kV变压器与上级电网相连,变压器低压侧电压为10.5 kV,配电网总有功负荷为5.24 MW,无功负荷为2.54 Mvar,负荷类型为工业用户;多能互补配电系统中有3个分布式光伏发电系统安装于工厂屋顶,分别位于节点3、节点4和节点6,节点5与节点8之间通过电转甲烷装置实现气电混合,同时节点5接入电转氢气装置、氢储能装置和氢燃料电池;日内运行时,氢储能装置初始容量设为额定装机容量的10%。算例具体参数见附录A表A1至表A3。

5.1 场景削减结果

本文在已知光照强度和负荷年历史曲线的基础上,根据第2节介绍的方法进行场景削减,每个季节的每种场景集合分别削减至2个,得到季节性日场景及其概率。以夏季为例,结果如图3所示。

图3 夏季日场景削减结果Fig.3 Results of daily load scenario reduction for summer

5.2 算例1:分布式光伏与气电混合协同规划

本算例假设每个节点拥有足够的屋顶场地铺设分布式光伏发电系统,分布式光伏发电、电转氢气装置、电转甲烷装置、氢储能装置和氢燃料电池的装机均为待求量。根据本文提出的方法计算得到的各种装置最佳装机容量是:1号、2号和3号分布式光伏发电系统装机容量分别达到3.200,4.844,3.158 MW,无需配置电转氢气装置、电转甲烷装置、氢储能装置和氢燃料电池。成本与收益计算结果见表1。

表1 分布式光伏容量与气电混合容量规划的成本与收益Table 1 Cost and benefit for optimal sizing of distributed PV and P2G

分析结果可见,在目前的设备市场价格、补贴机制、算例区域光照强度和负荷水平等条件下,对算例系统同时配置分布式光伏发电系统和气电混合系统时,仅配置光伏发电系统是综合经济效益最优的,配置气电混合系统暂不具有经济优势。产生这样的结果原因主要有:由电转氢气/甲烷、氢储能和氢燃料电池组成的气电混合联合系统在能量转化过程中损耗较大且投资成本较高。在这样的损耗和市场价格现状下,暂不适宜在配电网大规模推广气电混合多能互补配电系统。

5.3 算例2:分布式光伏高渗透率接入情况下的气电混合容量规划

本算例求解在配电网中1号、2号和3号分布式光伏发电系统的装机容量已经分别达到3,8,7 MW的情况下,如何通过配置电转甲烷装置、电转氢气装置、氢储能装置和氢燃料电池的最佳装机容量减少“弃光”,并使得系统投资成本和运行成本综合最低。根据本文提出的方法计算得到的各种装置最佳装机容量是:仅配置443 kW电转甲烷装置即可,无需配置电转氢气、氢储能和氢燃料电池。成本与收益计算结果见表1。

分析结果可见,典型算例中的节点3、节点4和节点6已高渗透率地接入了分布式光伏发电系统。在目前的市场价格条件下,仅对该系统配置一定的电转甲烷装置更具经济性,能源综合成本从50 756元/d降到50 620元/d。电转氢气装置、氢储能装置和氢燃料电池组成的联合系统暂不具备竞争优势,虽然等年值设备投资费用增长了,但由于电转甲烷对光伏消纳的促进作用,分布式光伏发电运营收益有所增加且节点用电成本降低。因此,在分布式光伏高渗透率地接入配电网且难以消纳的情况下,将原有系统改造成含分布式光伏与气电混合的多能互补配电系统能够一定程度地降低系统综合成本,促进光伏消纳。

5.4 参数灵敏度分析

各种市场价格参数对分布式光伏与气电混合在多能互补配电系统中的容量规划有重要影响。

本文在算例1的基础上,分析各种价格参数对结果的影响。

1)0.1元/(kW·h)分布式光伏补贴对应的分布式光伏容量规划结果的敏感度约为0.46 MW,0.1元/(kW·h)分布式光伏补贴对应的多能互补配电系统的综合成本敏感度约为3 396 元。

2)0.1元/(kW·h)用户电价对应的分布式光伏容量规划结果敏感度约为0.10 MW,0.1元/(kW·h)用户电价对应的多能互补配电系统的综合成本敏感度约为4 994 元。

由上述分析可见,分布式光伏容量规划结果对参数的敏感度排序是分布式光伏补贴高于用户电价;多能互补配电系统的综合成本对参数的敏感度排序是用户电价高于分布式光伏补贴。

此外,由前述计算可知,电转氢气装置、氢储能装置和氢燃料电池组成的联合系统由于设备市场价格较高,导致其尚不具备推广性。本文计算了电转氢气装置、氢燃料电池的单位容量价格对算例2中规划结果的影响,结果发现:当电转氢气装置和氢燃料电池价格分别下降到约2 500元/kW和5 000元/kW以下时,电转氢气装置、氢储能装置和氢燃料电池组成的联合系统才具有推广应用的经济可行性。

6 结语

本文设计了一种面向多能互补系统的分布式光伏与气电混合容量多场景规划方法,提出了采用对光照强度历史曲线和负荷历史曲线按照季节进行日曲线分类和场景削减的思想,将场景削减的结果作为后续的规划模型的输入数据。设计了一种含分布式光伏与气电混合的系统运行策略,采用了BFA对本文提出的模型进行求解。由计算分析可知,以目前的设备市场价格和补贴机制,气电混合系统尚不具备明显的综合效益优势,多数情况下在配电网中仅合理配置分布式光伏发电系统是综合经济效益最优的。但当分布式光伏发电容量已经冗余时,通过本文方法配置一定比例的气电混合系统可以降低系统综合成本。

值得指出的是,本文建立的数学模型假设分布式光伏发电补贴价格、上网电价和用电电价在项目全生命周期内不变。但是,受技术、经济和政策影响,这些敏感的价格参数可能变化,存在一定的不确定性,如何在规划问题中考虑这些不确定性是本文的下一步的工作。此外,虽然电转氢气装置、电转甲烷装置和氢燃料电池等装置的市场价格目前相对较高,但是随着技术进步和规模化发展,这些设备的市场价格有望遵循经典的“摩尔定律”而大幅下降,届时通过更新本文中的数学模型的关键参数,本文提出的方法对实际工程推广应用将能够发挥更大作用。

总体而言,对于现阶段含有分布式光伏发电的配电网而言,不宜盲目推广气电混合,应因地制宜,找到气电混合系统和多能互补配电系统的赢利点,合理配置其容量,才能实现系统综合成本最低。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 董朝阳,赵俊华,文福拴,等.从智能电网到能源互联网:基本概念与研究框架[J].电力系统自动化,2014,38(15):1-11.DOI:10.7500/AEPS20140613007.

DONG Zhaoyang, ZHAO Junhua, WEN Fushuan, et al. From smart grid to Energy Internet: basic concept and research framework[J]. Automation of Electric Power Systems, 2014, 38(15): 1-11. DOI: 10.7500/AEPS20140613007.

[2] 孙宏斌,潘昭光,郭庆来.多能流能量管理研究:挑战与展望[J].电力系统自动化,2016,40(15):1-8.DOI:10.7500/AEPS20160522006.

SUN Hongbin, PAN Zhaoguang, GUO Qinglai. Energy management for multi-energy flow: challenges and prospect[J]. Automation of Electric Power Systems, 2016, 40(15): 1-8. DOI: 10.7500/AEPS20160522006.

[3] 马溪原,郭晓斌,董朝阳,等.能源互联网的形态与试点构想[J].南方电网技术,2016,10(8):2-10.

MA Xiyuan, GUO Xiaobin, DONG Zhaoyang, et al. Features and demonstration prospect of energy internet[J]. Southern Power System Technology, 2016, 10(8): 2-10.

[4] 孙国强,陈霜,卫志农,等.计及相关性的电-气互联系统概率最优潮流[J].电力系统自动化,2015,39(21):11-17.DOI:10.7500/AEPS20150611006.

SUN Guoqiang, CHEN Shuang, WEI Zhinong, et al. Probabilistic optimal power flow of combined natural gas and electric system considering correlation[J]. Automation of Electric Power Systems, 2015, 39(21): 11-17. DOI: 10.7500/AEPS20150611006.

[5] QIU Jing, DONG Zhaoyang, ZHAO Junhua, et al. Low carbon oriented expansion planning of integrated gas and power systems[J]. IEEE Transactions on Power Systems, 2015, 30(2): 1035-1046.

[6] 徐宪东,贾宏杰,靳小龙,等.区域综合能源系统电/气/热混合潮流算法研究[J].中国电机工程学报,2015,35(14):3635-3642.

XU Xiandong, JIA Hongjie, JIN Xiaolong, et al. Study on hybrid heat-gas-power flow algorithm for integrated community energy system[J]. Proceedings of the CSEE, 2015, 35(14): 3635-3642.

[7] 黄炜,刘健,魏昊焜,等.分布式光伏电源极端可接入容量极限研究[J].电力系统保护与控制,2015,43(3):22-28.

HUANG Wei, LIU Jian, WEI Haokun, et al. Extreme capacity limitations of photovoltaic generators in distribution grids[J]. Power System Protection and Control, 2015, 43(3): 22-28.

[8] 刘健,同向前,潘忠美,等.考虑过电压因素时分布式光伏电源的准入容量[J].电力系统保护与控制,2014,42(6):45-51.

LIU Jian, TONG Xiangqian, PAN Zhongmei, et al. The maximum power of distributed PV generation according to over-voltage in distribution network[J]. Power System Protection and Control, 2014, 42(6): 45-51.

[9] 范元亮,赵波,江全元,等.过电压限制下分布式光伏电源最大允许接入峰值容量的计算[J].电力系统自动化,2012,36(17):40-44.

FAN Yuanliang, ZHAO Bo, JIANG Quanyuan, et al. Peak capacity calculation of distributed photovoltaic source with constraint of over-voltage[J]. Automation of Electric Power Systems, 2012, 36(17): 40-44.

[10] 章力,高元海,熊宁,等.考虑潮流倒送约束的分布式光伏电站选址定容规划[J].电力系统自动化,2014,38(17):43-48.DOI:10.7500/AEPS20140509005.

ZHANG Li, GAO Yuanhai, XIONG Ning, et al. Siting and sizing of distributed photovoltaic power station considering reverse power flow constraints[J]. Automation of Electric Power Systems, 2014, 38(17): 43-48. DOI: 10.7500/AEPS20140509005.

[11] KABIRIAN A, HEMMATI M R. A strategic planning model for natural gas transmission networks[J]. Energy Policy, 2007, 35(11): 5656-5670.

[14] SHARAN I, BALASUBRAMANIAN R. Integrated generation and transmission expansion planning including power and fuel transportation constraints[J]. Energy Policy, 2012, 43(2): 275-284

[15] UNSIHUAY-VILA C, MARANGON-LIMA J W, SOUZA A C, et al. A model to long-term, multiarea, multistage, and integrated expansion planning of electricity and natural gas systems[J]. IEEE Transactions on Power Systems, 2010, 25(2): 1154-1168.

[16] DUPACOVA J, GROWE-KUSKA N, ROMISCH W. Scenario reduction in stochastic programming: an approach using probability metrics[J]. Mathematical Programming Series B, 2003, 95(3): 493-511.

[17] 胡骅,徐冲,吴汕,等.影响用户侧分布式发电经济性因素分析[J].电力自动化设备,2008,28(5):29-33.

HU Hua, XU Chong, WU Shan, et al. Analysis of factors influencing economy of customer-side distributed generation[J]. Electric Power Automation Equipment, 2008, 28(5): 29-33.

[18] 王业磊,赵俊华,文福拴,等.具有电转气功能的多能源系统的市场均衡分析[J].电力系统自动化,2015,39(21):1-10.DOI:10.7500/AEPS20150623001.

WANG Yelei, ZHAO Junhua, WEN Fushuan, et al. Market equilibrium of multi-energy system with power-to-gas functions[J]. Automation of Electric Power Systems, 2015, 39(21): 1-10. DOI: 10.7500/AEPS20150623001.

[19] 肖峻,梁海深,王旭东,等.基于滤波的孤立微网多目标规划设计方法[J].电网技术,2014,38(3):596-602.

XIAO Jun, LIANG Haishen, WANG Xudong, et al. Multiple objective planning and designing of island microgrid based on filtering[J]. Power System Technology, 2014, 38(3): 596-602.

[20] 马溪原,吴耀文,方华亮,等.采用改进细菌觅食算法的风/光/储混合微电网电源优化配置[J].中国电机工程学报,2011,31(25):17-25.

MA Xiyuan, WU Yaowen, FANG Hualiang, et al. Optimal sizing of hybrid solar-wind distributed generation in an islanded microgrid using improved bacterial foraging algorithm[J]. Proceedings of the CSEE, 2011, 31(25): 17-25.

[21] 彭春华,谢鹏,詹骥文,等.基于改进细菌觅食算法的微网鲁棒经济调度[J].电网技术,2014,38(9):2392-2398.

PENG Chunhua, XIE Peng, ZHAN Jiwen, et al. Robust economic dispatch of microgrid using improved bacterial foraging algorithm[J]. Power System Technology, 2014, 38(9): 2392-2398.