基于改进灰色模型GM(1,1)的故障间隔时间预测
2018-03-12,
,
(福建工程学院 管理学院, 福建 福州 350118)
在长期运行过程中电梯会逐渐老化,直至发生故障,为确保电梯设备的正常运行,预防性维修显得尤为重要。现有的预防性维修主要是基于时间的预防性维修,定期对未失效的系统进行维护维修,以减少系统在使用过程中出现故障的可能性,降低由系统失效造成的损失。
灰色GM(1,1)模型[1-3]是解决不确定系统问题的有力工具之一,在灰色预测模型中,灰色
GM(1,1)模型由于具有模型简单,预测精确度较高等优点,被广泛应用于各类模型的预测中。但该模型对呈现随机波动的原始数据的预测效果不理想。为提高模型在该类型数据的预测效果,很多学者对GM(1,1)模型进行改进,邵延君等[4-5]分别采用基于新陈代谢组合模型和灰色线性回归组合模型对装备故障进行预测,马春茂等[6]采用基于灰色马尔可夫模型对装备故障间隔期进行预
测研究。Chen T[7]建立了马尔科夫灰色三角预测模型TGM(1,1),并以福建省的集装箱数量为例子,验证了该模型 的有效性和实用性;宁立沤[8]将三角函数-灰色GM(1,1)模型用于桥梁施工的监控;LI和ZHOU[9-10]采用三角函数-灰色GM(1,1)模型对数据序列进行预测,但由于该方法采用固定的周期值,根据灰色新息理论,数据序列的不断更新,积累到一定程度时周期可能会发生突变,采用固定的周期值显然不合理。因此,本文采用粒子群算法实时计算数据序列的周期,提出变周期三角函数-灰色GM(1,1)模型故障间隔预测算法。
1 灰色GM(1,1)模型
灰色GM(1,1)模型相关定义如下:
定义1[1]
设X(0)=(x(0)(1),x(0)(2),…,x(0)(n))
为非负序列, 称X(1)为X(0)的一阶累加生成序列,其中,
X(1)=(x(1)(1),x(1)(2),…,x(1)(n)),
称Z(1)为X(1)的紧邻均值生成序列,其中,Z(1)=(z(1)(2),z(1)(3),…,z(1)(n)),
k=2,3,…,n。
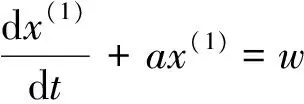
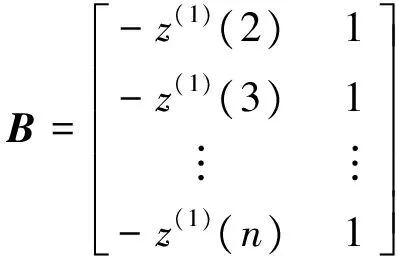
(1)
定义2 微分方程x(0)(k)+az(1)(k)=w中的z(1)(k)称为灰色GM(1,1)模型背景值。
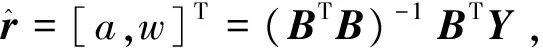
(2)
其时间响应序列为
(k=2,3,…,n)
(3)
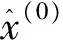
(k=2,3,…,n)
(4)
其中,-a为灰色GM(1,1)模型的发展系数;w为模型的灰色作用量。
2 基于三角函数的灰色GM(1,1)模型
由于灰色GM(1,1)模型构建的是指数递增或指数递减序列,为提高该模型在周期性数据的预测精度,可通过三角函数对原始数据与预测数据之间的残差序列建立修正模型,从而补偿灰色GM(1,1)模型最初的预测值。
定义3 假设通过灰色GM(1,1)模型得到的拟合值为
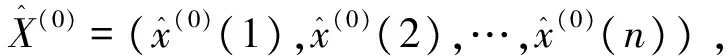
R(0)={r(0)(2),r(0)(3),…,r(0)(n)}
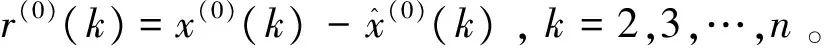
定义4[10]通过三角函数对残差序列进行建模,函数如下:
(5)
其中,εk是随机变量;T为主循环变化的周期参数。
3 基于变周期三角函数与灰色GM(1,1)模型预测算法
本文采用粒子群算法计算数据列的实时周期,提出变周期的三角函数,并与灰色GM(1,1)模型相结合,对故障间隔时间进行预测。
定义5 利用粒子群算法获得的周期序列T=(t2,t3,…,tn),则利用变周期三角函数对残差序列进行建模,函数如下:
(6)
其中,tk为k时刻的周期参数。
显然,可通过最小二乘估计方法计算式(6)。
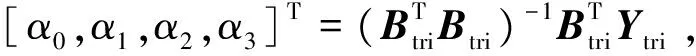
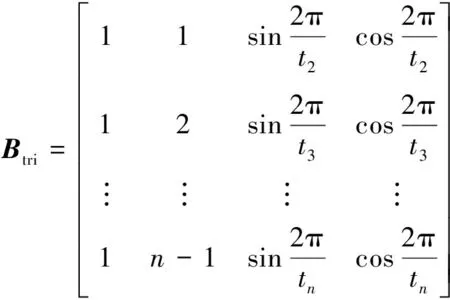
(7)
3.1 粒子群算法描述
假设在一个D维的搜索空间内,粒子数为n。算法通过迭代寻找最优解,第i个粒子位置表示为向量Xi=(xi1,xi2,…,xiD);第i个粒子飞行历史中的过去最优位置为Pi=(pi1,pi2,…,piD),整个种群过去最优位置Pg为所有Pi(i=1,2,3,…,n)中的最优,在每一次迭代中,粒子通过跟踪两个极值来更新自己,经过有限次迭代后最终收敛于全局的最好位置。粒子根据如下的公式来更新自己的速度和位置:
vid(t+1)=w·vid(t)+c1·r1·(pid(t)-
xid(t))+c2·r2·(pgd(t)-xid(t))
(8)
xid(t+1)=xid(t)+vid(t+1)
(9)
其中,c1和c2为学习因子,取c1=2,c2=2,r1和r2是介于[0,1]之间的随机数;w为惯性权重,可以调节算法的全局和局部寻优能力。
3.2 算法整体设计
根据以上所述,基于变周期三角函数的灰色GM(1,1)模型预测算法建模及求解如图1所示:
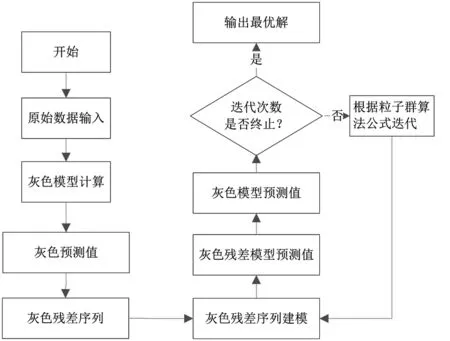
图1 算法流程图Fig.1 Flow chart of the algorithm
模型步骤具体描述如下:
1)给定初始周期向量T0,设定算法的迭代次数N,取定T=T0;
2)利用灰色GM(1,1)模型预测原始数据,得到预测值与原始值间的残差序列;
3)根据周期向量T0,利用公式(5)对残差序列建模,得到基于三角函数与灰色GM(1,1)模型的预测数列。
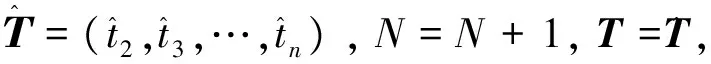
5)根据最终得到的周期T,利用公式(6),输出模型的最终预测值。
4 算例分析
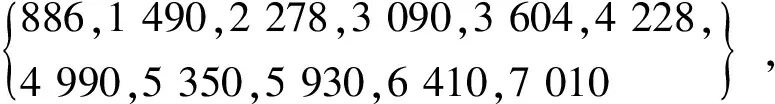
(单位:h),以故障间隔期的频数为横轴,以其发生的间隔期为纵轴,利用故障间隔期的数据依次做差,计算出故障频数与间隔时间,见表1。

表1 故障间隔时间与频数Tab.1 Interval time and frequency of failures
t1周期可以直接计算得出,见表2,首先给出初始向量T0=(t2,t3,…,tn)=(1,1,…,1),设置迭代次数N=100,以公式(6)为适应度函数,根据算法步骤最终获得的周期数列为Τ=(t2,t3,…,tn)。从表中可知,第9个间隔期周期最大为6,而第7个间隔期的周期最小,仅为2。
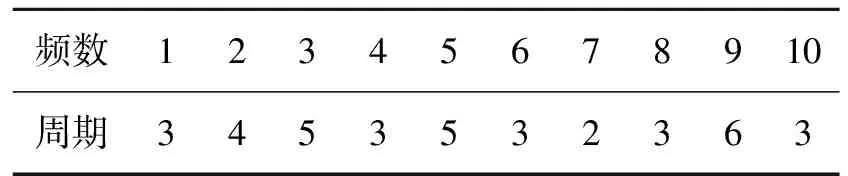
表2 故障间隔周期Tab.2 Interval periods of failures
将表2中的周期数列代入式(6),可得到故障间隔时间的拟合值,见表3。本文预测模型得到的平均相对误差为3.24%,将变周期三角函数与文献[10]三角函数的GM(1,1)模型预测结果进行比较,变周期三角函数模型的GM(1,1)精度明显优于文献[10]模型,见表3。
为直观分析表3中两种算法的预测结果,采用图形的方式进行描述,见图2。图2中,三角函数的GM(1,1)模型预测算法的拟合值与原始值的偏移值较大,拟合效果不如变周期三角函数GM(1,1)模型预测算法。
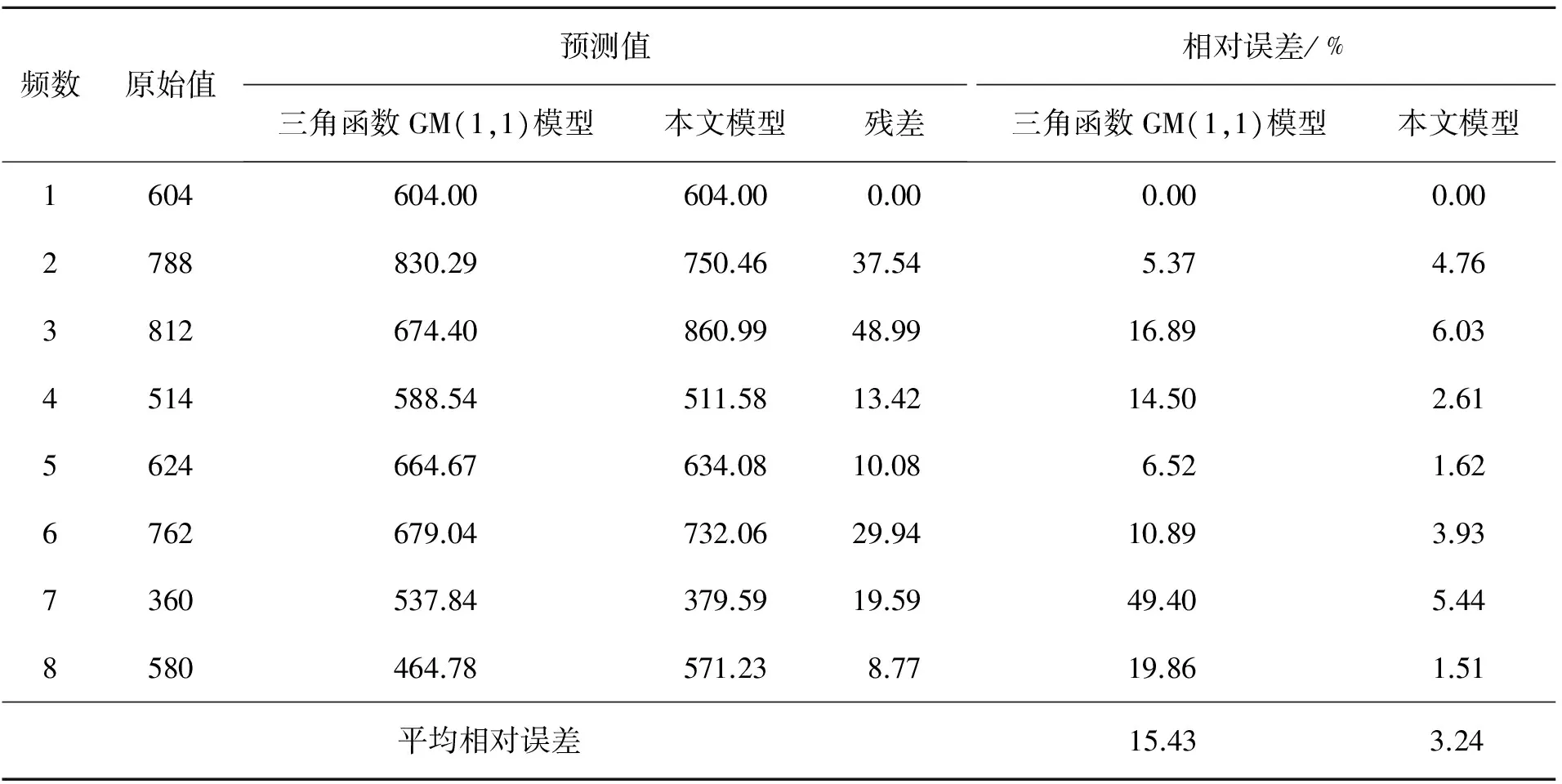
表3 基于变周期三角函数的GM(1,1)模型拟合结果Tab.3 Fitting results of GM (1, 1) based on the trigonometric function with variable periods
根据表3,对之后的两次故障时间间隔进行预测,预测的周期取值设定为前面8个周期的平均值,T预测结果见表4与图3,三角函数GM(1,1)模型在第9个故障间隔时间的预测结果误差较大,整体平均相对误差为24.16%。而本文预测模型对应的平均相对误差为3.24%,比三角函数的GM(1,1)模型低20.92个百分比。
变周期三角函数的GM(1,1)模型第9个与第10个故障时间间隔预测值与原始数据的比较结果见图3。第9个故障时间间隔预测偏差极小,第10个故障间隔时间的预测值与原始值的偏移量也在理想范围。整体预测效果理想。
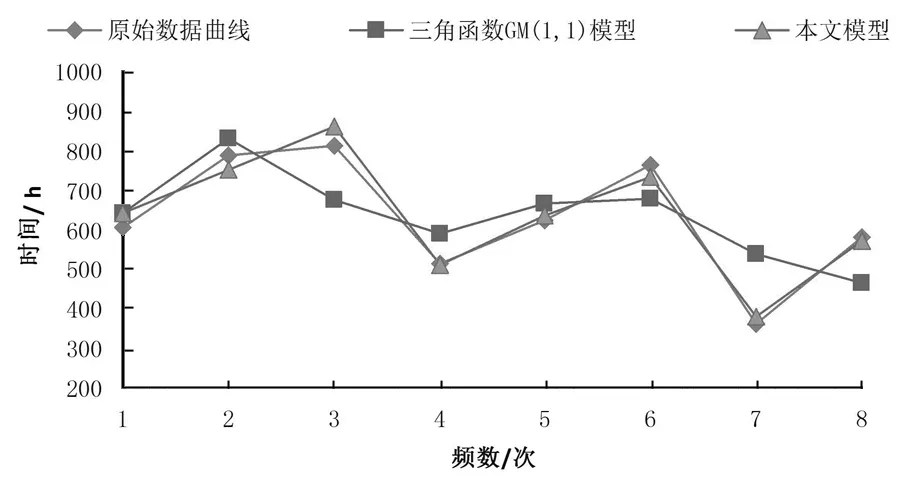
图2 故障间隔时间拟合值Fig.2 Fitting values of failure interval time
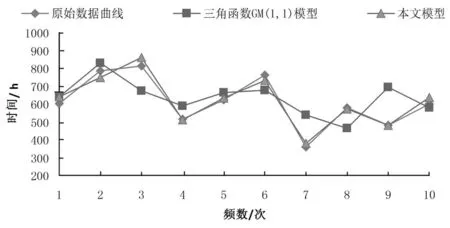
图3 故障间隔时间预测图Fig.3 Prediction graph of failure interval time

频数原始值预测值三角函数的GM(1,1)模型本文模型相对误差/﹪三角函数的GM(1,1)模型本文模型9480695.67480.9644.930.210600579.63637.793.396.29平均相对误差24.163.24
5 结论
为提高灰色GM(1,1)模型在故障间隔数据序列的预测精度,本文利用灰色GM(1,1)模型预测原始数据列,获得灰色模型预测值与原始数据的残差序列;根据数据序列的傅里叶变换求解原理,利用三角函数对残差序列进行修正,并在修正前利用粒子群算法获得残差序列各数据点对应的周期序列,提出基于变周期三角函数的灰色GM(1,1)预测模型。采用故障时间间隔对本文预测算法进行验证,并与固定周期的三角函数灰色预测GM(1,1)模型相比较,算例结果显示,本文预测模型具有更低的平均相对误差,预测效果明显提高。
[1] 邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002.
[2] 刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].3版.北京:科学出版社,2004.
[3] 邓聚龙.灰预测与灰决策[M].武汉:华中科技大学出版社,2002.
[4] 邵延君,潘宏侠,马春茂,等.基于新陈代谢组合模型的装备故障预测[J].振动、测试与诊断,2015,35(2):359-362.
[5] 邵延君,潘宏侠,马春茂,等.基于灰色线性回归组合模型的故障率预测[J].振动、测试与诊断,2014,34(4):664-667.
[6] 马春茂,邵延君,潘宏侠,等.基于灰色马尔可夫模型的装备故障间隔期预测研究[J].兵工学报,2013,34(9):1193-1196.
[7] CHEN T, ZHAO S J. Improved trigonometric grey prediction and application[J]. Advanced Materials Research, 2014, 912-914: 1276-1278.
[8] 宁立沤.基于改进灰色GM(1,1)模型的桥梁施工监控方法[J].建筑建材装饰,2016(13):233-237.
[9] LI Junliang, LIAO Runquan. Generalized accumulated GM (1,1) cosine model and its application[J]. Grey Systems Theory & Application, 2011, 2(2): 242 - 245.
[10] ZHOU P, ANG B W, POH K L. A trigonometric grey prediction approach to forecasting electricity demand[J]. Energy, 2006, 31(14): 2839-2847.
