四旋翼无人机高度控制
——基于CNF与自适应非光滑控制
2018-03-12,,,
, , ,
(1.福建工程学院 信息科学与工程学院, 福建 福州350118; 2.中国电子科技集团公司第五十八研究所, 江苏 无锡 214035; 3.福建对外经济贸易职业技术学院 信息技术系, 福建 福州350016)
四旋翼无人飞行器(quadrotor UAV)是一种能够垂直起降及以各种姿态飞行(如:悬停、前飞、侧飞和倒飞等)的无人飞行器。相比传统固定翼和直升机式无人飞行器,四旋翼无人飞行器具有体积小、重量轻、结构简单、可垂直起降等特点,近年来随着微机电系统(MEMS)等技术的发展,四旋翼无人飞行器技术特别是微型四旋翼无人机技术快速发展得到了广泛应用[1-2]。
随着四旋翼无人飞行器应用的发展,特别是高度受限环境等应用对四旋翼无人飞行器在高度控制过程提出更高要求,如过程中快速到达给定位置,不能出现过大超调,且对外部扰动及参数不确定等影响具有自适应补偿与抑制能力,跟踪误差较小等。显然,传统的PID、LQ等[3-4]控制方法难以满足要求。文献[5-6]针对四旋翼无人飞行器设计反步滑模控制,其中文献[6]利用模糊逻辑来优化系统“抖振”,该方法能够有效改善控制品质,但未能彻底解决“抖振”问题。文献[7]将非线性动态逆的思想设计跟踪控制器来提高控制精度与鲁棒性,但该方法未给出参数不确定及外部扰动下的测试结果。为进一步提高控制品质,自适应控制方法被引入:Dydek等将模型参考自适应控制应用于四旋翼无人机的飞行控制中[8],仿真与实验表明该方法通过对不确定参数的在线估计及补偿能减小跟踪误差及超调,但该方法未考虑外部扰动影响。李劲松等引入自适应优化控制方法(adaptive control optimization, ACO)[9-10],将控制问题转化为优化问题,通过迭代优化求最优系统权系数,通过实验证明了该方法的有效性,但该方法稳态误差仍待改善,且缺少严格的理论分析。文献[11]针对参数不确定设计了一种浸入与不变(immersion and invariance, I&I)自适应控制方法,并通过仿真与实验验证方法的有效性,但外部扰动影响下该方法有效性有待进一步研究。文献[12]针对模型误差及外部扰动影响,基于Lyapunov方法设计了一种鲁棒自适应控制方法,并通过实验验证了方法的有效性,但其控制性能仍存在提升空间。此外,以上研究大都侧重于轨迹跟踪控制研究,没有给出轨迹生成方法,因此无法判断方法是否能实现快速到达给定位置且超调较小。
针对四旋翼无人飞行器在参数不确定及外部扰动影响下的高性能高度控制问题,以实现飞行器在约束空间内的快速高度机动为目标,综合考虑高度机动轨迹规划与控制问题。受文献[13]等启示,设计了一种基于CNF算法和自适应非光滑控制方法的四旋翼无人飞行器高度控制方法,通过轨迹规划和轨迹跟踪控制相结合的方法克服模型误差及外部扰动影响,实现快速、较小超调的高性能高度控制。
1 预备知识
1.1 四旋翼无人飞行器动力学模型
对于常见的“X”形四旋翼无人飞行器,假设:机身为刚性结构体并呈对称分布,螺旋桨为刚性体,转动无形变且位置固定。记x、y、z是惯性坐标系下飞行器的质心位置;φ、θ、ψ是惯性坐标系下飞行器的姿态角;Ix、Iy、Iz分别是机体绕三轴的转动惯量;m为机体质量;l为机体中心到旋翼中心的距离;b、d为旋翼的升力和阻力系数;g重力加速度;则其动力学模型可以描述为[1]:
(1)
其中,U1、U2、U3、U4分别是4个通道的虚拟控制量,由4个旋翼的转速决定:
(2)
本文针对其中的高度控制问题开展研究,由理想动力学模型可知,四旋翼无人飞行器的垂直通道是一个与姿态存在耦合的二阶系统,考虑实际应用中存在的参数不确定及建模外因素影响,动力学模型可以描述为:
(3)
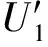
记pz=(mn+mu)/(bn+bu),将式(3)变换为如下形式:
(4)
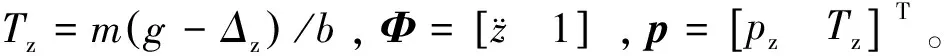
(5)
其中,pzn=mn/bn,Tzn=mngn/bn;pzu=m/b-pzn;Tzu=Tz-mngn/bn。
将式(5)整理为:
(6)
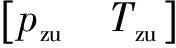
1.2 新形式Barbalate引理
对于一致连续函数x(t),如果存在标量函数V和M满足如下条件[14]:
(1)V有下界;
(2)M为连续正定且径向无界;
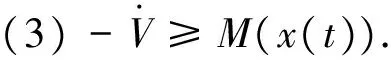
那么,当t→时,x(t)→0。
2 高度轨迹生成与控制器设计
2.1 基于CNF的高度轨迹生成方法
实际飞行任务往往要求四旋翼无人飞行器快速到达指定高度,而在空间受限环境中,如:屋顶、悬挂物等影响下,飞行器高度机动过程中不容许出现严重超调(过度超过指定高度可能导致碰撞等危险)。因此需要预先进行高度轨迹规划,传统采用的规划方法往往没有考虑飞行器的动力学特性且算法比较复杂。针对该问题,本文将利用CNF控制器的超调小,算法简单的特点解决高度机动轨迹规划问题,方法设计如下。
记:a1=(cosφcosθ)bU1/m,则式(1)中四旋翼无人飞行器的垂直通道动力学模型可以改写为:
(7)
由于四旋翼无人飞行器物理结构及动力设计的特点,其旋翼一般无法反转,且旋翼存在最低转速要求[9],即0<ωmin≤ωi<ωmax,i=1,2,3,4,对于U1有:
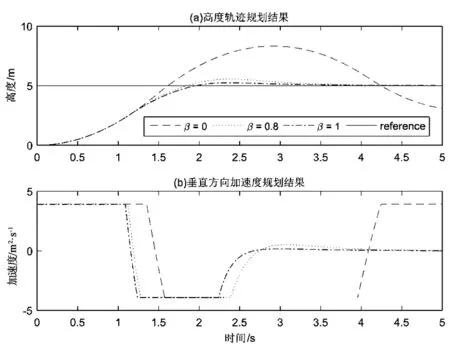
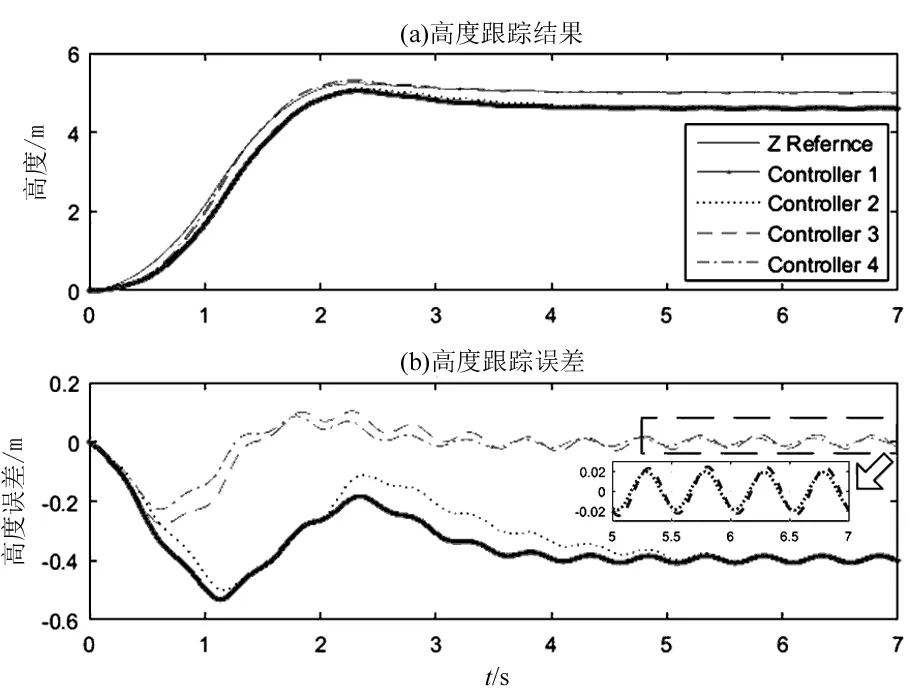
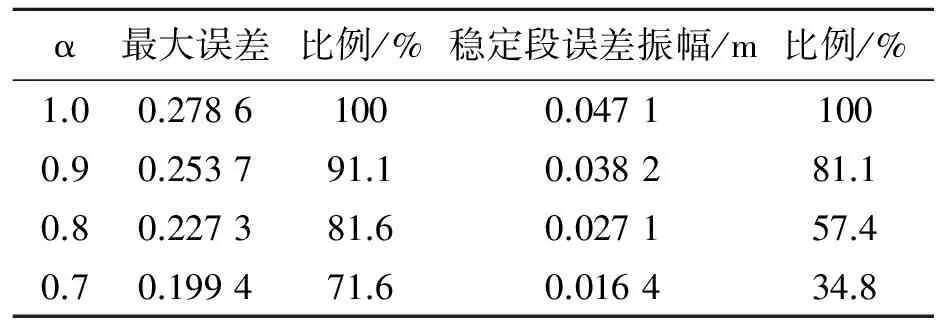
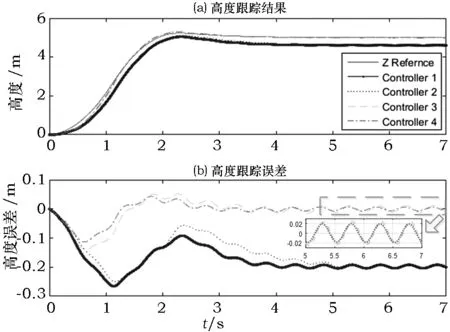
0 (8) 则: a1min-g≤az≤a1max-g (9) 其中,a1max=a1|U1=U1max,a1min=a1|U1=U1min,且a1min-g<0。显然存在α>0,使得-αg≤az≤αg成立,将以上关系作为高度轨迹规划时的保守约束条件,则垂直通道的动力学模型应该改写为: (10) (11) 考虑常见的阶跃高度控制问题,如式(10)和式(11)所示的高度轨迹规划问题可以转换为输入受限的线性系统控制问题,可以设计复合非线性控制器CNF,并依据离散动力学模型通过递推生成规划轨迹。具体步骤如下: 步骤1 根据CNF控制器设计方法,分别设计控制器的线性控制和非线性控制部分。 u=uL+uN (12) 其中线性控制器部分为: uL=Fx+Gr (13) 非线性控制器部分为: uN=ρ(r,y)BTP(A+BF)[x-xe] (14) 其中: (15) ρ(r,y)=-η(e-[1-y/r]-0.367 9). (16) 受篇幅所限分析及证明过程省略,详见文献[13-14]。 步骤2 将系统离散化 首先将动力学方程整理为状态空间方程形式,即: (17) 离散化可以得到: (18) 最后,根据设计得到的CNF控制器及当前高度、给定高度等,只需选定参数α、F和η(调整上升时间和超调,可以根据工作环境及要求离线预先生成,参数选定方法详见文献[13-14]),再根据离散状态空间方程、状态初值及控制律(式(12)-(16))递推生成高度轨迹。 利用CNF方法可以生成到达指定高度的合理轨迹,为了使飞行器按照给定轨迹到达指定高度,需要设计一个高性能的高度轨迹跟踪控制器,控制器需要克服应用中常见的参数不确定及外部扰动等影响因素。因此,本文将设计一种自适应非光滑控制器,sig(ξ)α=|ξ|αsign(ξ)设计步骤如下: 步骤1 控制器设计 (19) 为保证ζ1收敛,选取虚拟控制量为: β=x2r-k1sig(ζ1)α (20) 其中,设计参数k1>0,0<α<1。 将式(20)代入式(17)得: (21) 进一步选取Lyapunov函数: (22) (23) 将式(6)代入并整理得: (24) 选择控制为: (25) 其中,设计参数k2>0。则式(24)可以改写为: (26) 步骤2 自适应律设计 根据式(26),如果取: (27) 显然有: (28) (29) 定理考虑由系统(式(5)),控制器(式(25))及自适应律(式(29))所构成的闭环系统,当t→,ζ1→0、ζ2→0,即x1→x1r、x2→x2r。 证明 定义标量函数: M(ζ1,ζ2)=k1ζ1sig(ζ1)α+k2ζ2sig(ζ2)α (30) 根据式(28)易得: (31) 结合定义及式(20)有: (32) 将式(24)代入式(6)并整理可得: (33) 结合定义有: (34) 根据定义(30),M(ζ1,ζ2)为连续正定且径向无界。根据1.2中引理可得:当t→时,ζ1→0、ζ2→0,即x1→x1r、x2→x2r。 (35) 这里:λ为很小正数。 图1 四旋翼无人机高度控制Simulink模型Fig.1 Simulink model of altitude control for quadrotor UAV 图2 高度轨迹规划结果Fig.2 Results of altitude trajectory plan 为了验证所设计的自适应非光滑高度控制的性能,设计如下系列实验:(1)α=1.0,且自适应律关闭时,即将控制器退化为普通的反步控制器,这里简称为Controller 1;(2)α=0.9,且自适应律关闭时,即将控制器退化为普通的非光滑控制器,这里简称为Controller 2;(3)α=1.0,且自适应律开启时,即将控制器退化为普通的反步控制器,这里简称为Controller 3;(4)α=0.9,且自适应律开启时,这里简称为Controller 4;图3给出了4种实验结果的对比情况,可以看出Controller 1控制品质最差;相比之下Controller 2控制品质有所改善;由于自适应律的作用,Controller 3和Controller 4的控制品质相比Controller 1和Controller 2有明显提高,二者相比,最大跟踪误差相比:Controller 3最大跟踪误差为0.278 7 m,而Controller 4为0.227 3 m;稳定阶段跟踪误差相比:Controller 3稳定段误差振幅为0.047 1 m,Controller 4为0.027 1 m。显然Controller 4的控制品质更佳。因此,自适应非光滑控制对于参数失配及外部扰动具有更好的鲁棒性。 图3给出了4种仿真实验结果及对比情况。 图3 高度控制实验结果Fig.3 Results of altitude control experiments 可以看出Controller 1控制品质最差;相比之下Controller 2控制品质有所改善;由于自适应律的作用,Controller 3和Controller 4的控制品质相较Controller 1和Controller 2有明显提高,二者相比,最大跟踪误差方面:Controller 3最大跟踪误差为0.278 7 m,而Controller 4为0.227 3 m,稳定阶段跟踪误差方面:Controller 3稳定段控制误差振幅为0.047 1 m,而Controller 4为0.027 1 m。综上,Controller 4的控制品质最佳,自适应非光滑控制对于参数失配及外部扰动具有更好的鲁棒性,可以实现更高精度的高度轨迹及定高控制。 注2:由于忽略了外部扰动的时变性,因此自适应非光滑无法实现完美补偿。 注3:本文所提出自适应非光滑控制方法运行过程中,理论上只能保证跟踪误差趋于零,但无法保证估计结果收敛于真实值。研究表明,只有输入信号满足持续激励条件时估计值才会逼近真值[15]。 进一步为考察分数幂次对自适应非光滑控制的影响,选择α为1.0、0.9、0.8、0.7,重复上述仿真实验(其他参数不变,具体参数见上文),结果及对比如图4所示。由结果可知减小α,可以减小最大跟踪误差与稳定段误差(见表1,其中“比例”一项指不同α值时的误差与α=1.0时的误差之比)。对于实际应用中α过小可能会引起系统抖颤,因此α需要根据实际情况做出选择。 表1不同α时高度控制误差对比 Tab.1Comparisonoferrorsofaltitudecontrolwithdifferentα α最大误差比例/%稳定段误差振幅/m比例/%1.00.27861000.04711000.90.253791.10.038281.10.80.227381.60.027157.40.70.199471.60.016434.8 图4 不同α时高度控制实验结果Fig.4 Results of altitude control experiments with different α 针对动力学参数及外部扰动影响下的四旋翼无人机高度控制问题展开研究。设计了一种基于CNF与自适应非光滑控制的高度控制方法,并借助仿真及对比验证本文方法的有效性。结果表明,本文所设计方法可以快速地实现高度轨迹规划,且所设计的自适应非光滑高度轨迹控制方法可以有效改善控制品质,算法简单易于实现,无需准确的系统参数,适合应用于高度受限环境中的四旋翼无人机的高度控制。 [1] BOUABDALLAH S, MURRIERI P, SIEGWART R. Design and control of an indoor micro quadrotor[C]∥2004 IEEE International Conference on Robotics and Automation, IEEE, 2004: 4393-4398. [2] KENDOUL F. Survey of advances in guidance, navigation, and control of unmanned rotorcraft systems[J]. Journal of Field Robotics, 2012, 29(2): 315-378. [3] BOUABDALLAH S, NOTH A, SIEGWART R. PID vs LQ control techniques applied to an indoor micro quadrotor[C]∥ International Conference on Intelligent Robots and Systems. IEEE, 2004: 2451-2456. [4] KHATOON S, SHAHID M, IBRAHEEM, et al. Dynamic modeling and stabilization of quadrotor using PID controller[C]∥ International Conference on Advances in Computing, Communications and Informatics, 2014: 746-750. [5] KHEBBACHE H, TADJINE M. Robust fuzzy backstepping sliding mode controller for a quadrotor unmanned aerial vehicle[J]. Control Engineering & Applied Informatics, 2013, 15(2): 3-11. [6] CHEN F, JIANG R, ZHANG K, et al. Robust backstepping sliding-mode control and observer-based fault estimation for a quadrotor UAV[J]. IEEE Transactions on Industrial Electronics, 2016, 63(8): 5044-5056. [7] 许璟,蔡晨晓,李勇奇,等.小型四旋翼无人机双闭环轨迹跟踪与控制[J].控制理论与应用,2015,32(10):1335-1342. [8] DYDEK Z T, ANNASWAMY A M, LAVRETSKY E. Adaptive control of quadrotor UAVs: a design trade study with flight evaluations[J]. IEEE Transactions on Control Systems Technology, 2013, 21(4): 1400-1406. [9] 李劲松.四旋翼小型无人直升机自适应逆控制研究[D].上海:上海交通大学,2014. [10] 李劲松,杨炼,王乐天.小型四旋翼无人直升机自适应优化控制[J].上海交通大学学报,2015,49(2):202-208. [11] ZHAO B, XIAN B, ZHANG Y, et al. Nonlinear robust adaptive tracking control of a quadrotor UAV via immersion and invariance methodology[J]. IEEE Transactions on Industrial Electronics, 2015, 62(5): 2891-2902. [12] ISLAM S, LIU P X, EL SADDIK A. Robust control of four-rotor unmanned aerial vehicle with disturbance uncertainty[J]. IEEE Transactions on Industrial Electronics, 2015, 62(3): 1563-1571. [13] LAN W, THUM C K, CHEN B M. A hard-disk-drive servo system design using composite nonlinear-feedback control with optimal nonlinear gain tuning methods[J]. IEEE Transactions on Industrial Electronics, 2010, 57(5): 1735-1745. [14] CHEN B M, LEE T H, PENG K, et al. Composite nonlinear feedback control for linear systems with input saturation: theory and an application[J]. IEEE Transactions on Automatic Control, 2003, 48(3): 427-439. [15] 斯洛坦(SLOTINE J E),李(LI W),程代展.应用非线性控制[M].北京:机械工业出版社,2006. [16] HOU M, DUAN G, GUO M. New versions of Barbalat’s lemma with applications[J]. Journal of Control Theory and Applications, 2010, 8(4): 545-547.
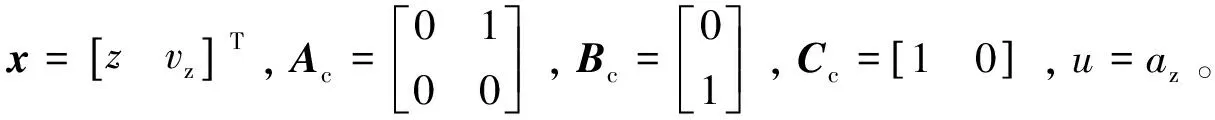
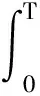
2.2 自适应非光滑控制器设计与分析
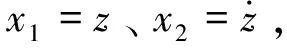
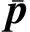
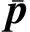
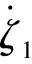
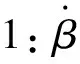
3 仿真实验与分析
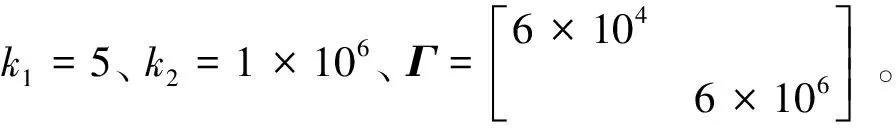

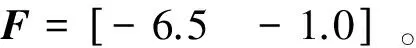
4 结 语
