定时维修间隔期的优化计算方法

庞名泰，郭金茂，张耀辉

(装甲兵工程学院，北京 100072)

对于现在复杂装备而言，进行事后维修对维修费用来讲是不合理的，对安全来讲也是存在重大隐患的。因此，现行装备维修方案一般分为定时维修和非定时维修两种。定时维修是一种以预防维修为主的维修措施;而非定时维修是以突发性故障抢修为主。传统的定时维修间隔期的确定一般以经验时间为衡量标准。但是实际上，由于维修间隔期确定方法的老化，传统的经验时间作为定时维修时间往往造成某些系统或部件在定时预防维修时发生维修过剩或者维修不足的问题。此时，维修间隔期达不到预防维修的目的。本文通过分析维修过剩情形下的装备维修间隔期经济模型，提出了一种新的定时预防维修时间的确定方法。并给出了算例分析。

1 假设和参数

1)假设。装备工作到原始维修间隔期T时，运行良好无故障;继续运行T1时间后，进行定时维修，系统回复如新;装备运行期间故障率随工作时间而变化，为变量。相对于维修间隔期T的检修时间和更换时间很小可以忽略不计。

2)参数。R(T)表示T时刻装备可靠度，即T时间内装备不发生故障的概率，0≤R(T)≤1;Cp为定时更换一次的平均费用;Cf为故障后更换一次的平均费用;λ为故障率，服从威布尔分布;m是表征分布曲线形状的参数，称为形状参数，m≥3.5时，曲线趋于正态分布的情况，其故障大致相当于浴盆曲线耗损故障期;t0是表征坐标尺度的参数，称为尺度参数，影响分布曲线坐标轴的标尺比例。

2 维修间隔期模型建立

假设在原有定时维修间隔期T内不进行维修，安排在其后的某段时间T1时进行维修，则装备此时以工作时间为T+T1，则有:到达维修间隔期 T时装备无故障，即可靠度为R(T)=1，到达T+T1时，装备的可靠度:

装备的不可靠度为1-R(T+T1|T)，则在T+T1时间内，进行维修的总费用:

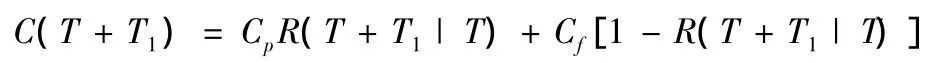
在T+T1时间内，装备的平均工作时间:

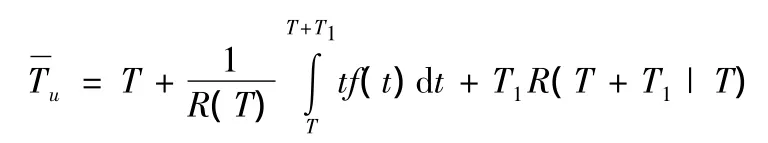
则在T+T1时间内，装备的单位工作时间费用:

由式(1)可知，要想确定T1，只需知道装备的可靠度函数服从何种分布即可。因装备寿命和维修时间是随机变量，因此，其有关概率分布及性质成为进行可靠性维修性分析的数学基础。在故障率有递增、递减情况时，可用威布尔分布来描述，所以定时维修的装备寿命和维修时间也可当作威布尔分布处理。

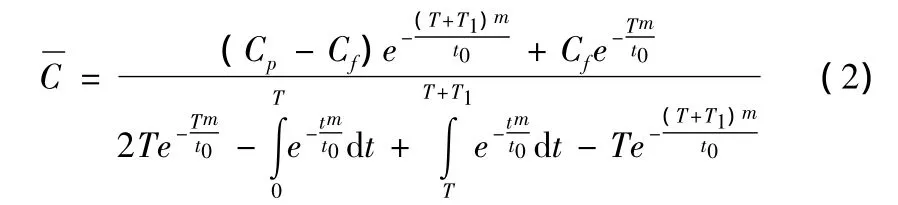
式(2)中，原有定时维修间隔期T已知，装备寿命服从威布尔分布，所以形状参数m和尺度参数t0已知，装备维修间隔期内预防维修费用Cp和故障维修费用Cf已知。只有T1未知，即单变量求解。欲求最小维修费用为目标的最佳更换间隔期T+T1，只需将上式对T1求导，并令其为零即可。

3 算例分析

现已知某型装备发动机到规定间隔期进行检测时发现发动机无故障，为提高装备利用率，充分发挥装备效能，需要合理确定其维修间隔期。发动机原有定时小修间隔期为220摩托小时，预防性全部定时更换费用为Cp=0.8万元，，故障后维修更换费用为Cf=1万元，，发动机寿命服从威布尔分布m=3.5，t0=1，求到达定时维修间隔期后，最佳持续运行时间T1，使装备在整个维修间隔期内单位时间内的平均费用最小。

将给定条件中 T、Cp、Cf、m、t0代入式(2)中，得由 Matlab数值计算，可以解出相应的T1，如图1所示。

由此可以得出单位时间内的平均费用为0.24万元和装备继续运行时间24摩托小时。从而可以得出最佳的维修间隔期为220+24=246 h。

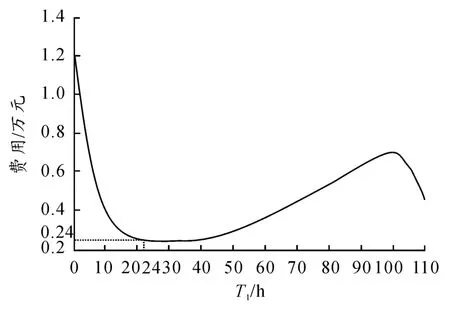
图1 单位时间内的平均费用和装备继续运行时间之间的关系

4 结束语

本文研究表明，由于原始装备维修间隔期的确定大多依靠传统经验时间求平均值而得，方法相对来说比较落后，因此给新形势下装备定时维修间隔期的确定带来一定的难度。针对这种实际情况，文中从原有装备维修间隔期过小，适当增大维修间隔期角度出发，考虑增大运行时间，应用Matlab进行数据分析，计算最佳的维修间隔期，以满足费用最小的原则下确定维修间隔期。论文所研究的内容，可用于新型装备刚投入使用时，数据缺乏情况下修间隔期的确定。

［1］张耀辉，张仕新，刘颖.装备维修工程［M］.北京：装甲兵工程学院，2003：1-6.

［2］张耀辉.装备维修技术［M］.北京：国防工业出版社，2008：12.

［3］姬东朝，肖明清.一种新的最小维修优化数学模型的建立［J］.航空计算技术，2007，32(3)：31-33.

［4］涂海宁，朱永国，刘建胜.设备维修方案优化［J］.机械设计与制造，2006(8)：173-174.

［5］苏春，黄茁，许映秋.基于遗传算法和蒙特卡洛仿真的设备维修策略优化［J］.东南大学学报，2006，36(6)：941-945.

［6］Pascual P，Omega J H.Optimal Replacement and Over-haul Decisions with Imperfect Maintenance and Warranty Contracts［J］.Reliability Engineering and System Safety，2006，91：241-248.

［7］高崎，李有为，郝冰.基于三级维修体制的设备可用度模型［J］.火力与指挥控制，2010(5)：107-109.