经编纱线动态张力评价指标
2018-03-12缪旭红江南大学教育部针织技术工程研究中心江苏无锡214122
胡 瑜, 刘 行, 缪旭红(江南大学 教育部针织技术工程研究中心, 江苏 无锡 214122)
在经编织造过程中,纱线张力控制尤为重要。张力过大,纱线被迫拉伸,强力下降,易造成断纱,影响织造效率,严重时还会损伤成圈机件;张力过小,纱线间相互黏连,纱线软趴,无法正常垫纱成圈。因此在经编织造过程中,合理控制纱线张力至关重要,直接影响到坯布质量、生产效率以及后续的正常加工[1]。合理控制纱线张力就需对纱线张力进行测量,并通过合适的方法进行评价。建立了合适的评价方法后就可对不同情况下的纱线张力进行评价比较,为进一步研究经编纱线张力的影响因素奠定基础。
近几年,随着测试技术不断发展,高频实时测试的张力数据更加精确,数据量也越来越大,虽然大数据可为我们带来更全面的信息,但是如何分析这些数据并对纱线动态张力进行评价却产生了难题:冯勋伟[2]、刘苏[3]、Mikolajczyk[4]分别通过比较张力的最大值、最小值来评价机速、原料、送经量等对张力的影响;陈红霞等[5]提出用标准差来评价张力整体的波动情况;但用这些指标来评价高频张力测试系统得到的实时动态张力数据还不够准确,对动态张力数据所包含的信息以及经编纱线动态张力波动规律的反映还有所欠缺。本文根据经编纱线动态张力的特点,提出一种新的评价方法用于张力整体波动情况的评价,并通过实验进行验证,为进一步研究经编纱线动态张力提供一定理论基础。
1 经编张力评价方法
1.1 概率密度曲线
概率密度曲线可用来描述连续型随机变量瞬时值落在某指定范围内的概率[6-7]。将所测某段时间内实时的纱线张力数据进行概率密度分析,对得到的频率分布直方图进行拟合得到概率密度曲线,通过对曲线形状的分析,得出这段时间内各张力值大小的分布情况,从而对张力整体的波动做出定性的评价。
1.2 峰度与偏度
概率密度曲线只能定性地评价纱线张力的整体波动情况,不能作定量分析,因此引入峰度和偏度这2个指标描述数据的分布形状[8],通过比较这2个值的大小,来定量分析张力的整体波动程度。
设x1,x2,…,xn是来自总体x的一个样本,总体x的峰度α为

总体x的偏度β为
峰度α反映各数据分布的尾部厚度,峰度越大,数据分布的尾部越厚,当偏度一定,峰度越大,说明张力波动越大。偏度β反映数据分布的尾部在其中一侧上是否有拉长趋势:偏度为0表示数据相对均匀地分布在平均值的两侧,其形态与正态分布的的偏斜一致;偏度大于0表示数据分布的右侧尾部要比左侧长;偏度小于0表示数据分布的左侧尾部要比右侧长[9-10]。当峰度一定,偏度绝对值越大,表示数据分布其中一侧的拉长程度更大,张力波动越大[11]。因此对于经编纱线张力,峰度越小,数据分布尾部越细,偏度越接近于0,数据分布的左右两侧拉长趋势小,数据更加集中,极端值更少。峰度越小,偏度越接近于0,张力分布越均衡,张力波动越小。通过结合峰度偏度的大小,可对不同工艺情况下的张力进行比较分析。
2 经纱张力的测试与评价
2.1 实验原料与仪器
仪器设备:E36的HKS3-M型特里科经编机(德国Karl Mayer有限公司);TS1-200-A2-CE1型张力仪(德国Schmidt有限公司);SCM01型四通道声振分析仪和LMS Test.Lab分析软件(比利时LMS公司)。
实验原料:采用3把梳编织,GB1满穿83.3 dtex/144 f有光扁平涤纶,GB2和GB3满穿33.3 dtex/12 f涤纶全牵伸丝(FDY)。
2.2 测试方法
将张力仪和四通道声振分析仪按照测试要求,在经编机上搭建成完整的纱线张力测试系统。具体系统构架如图1所示。
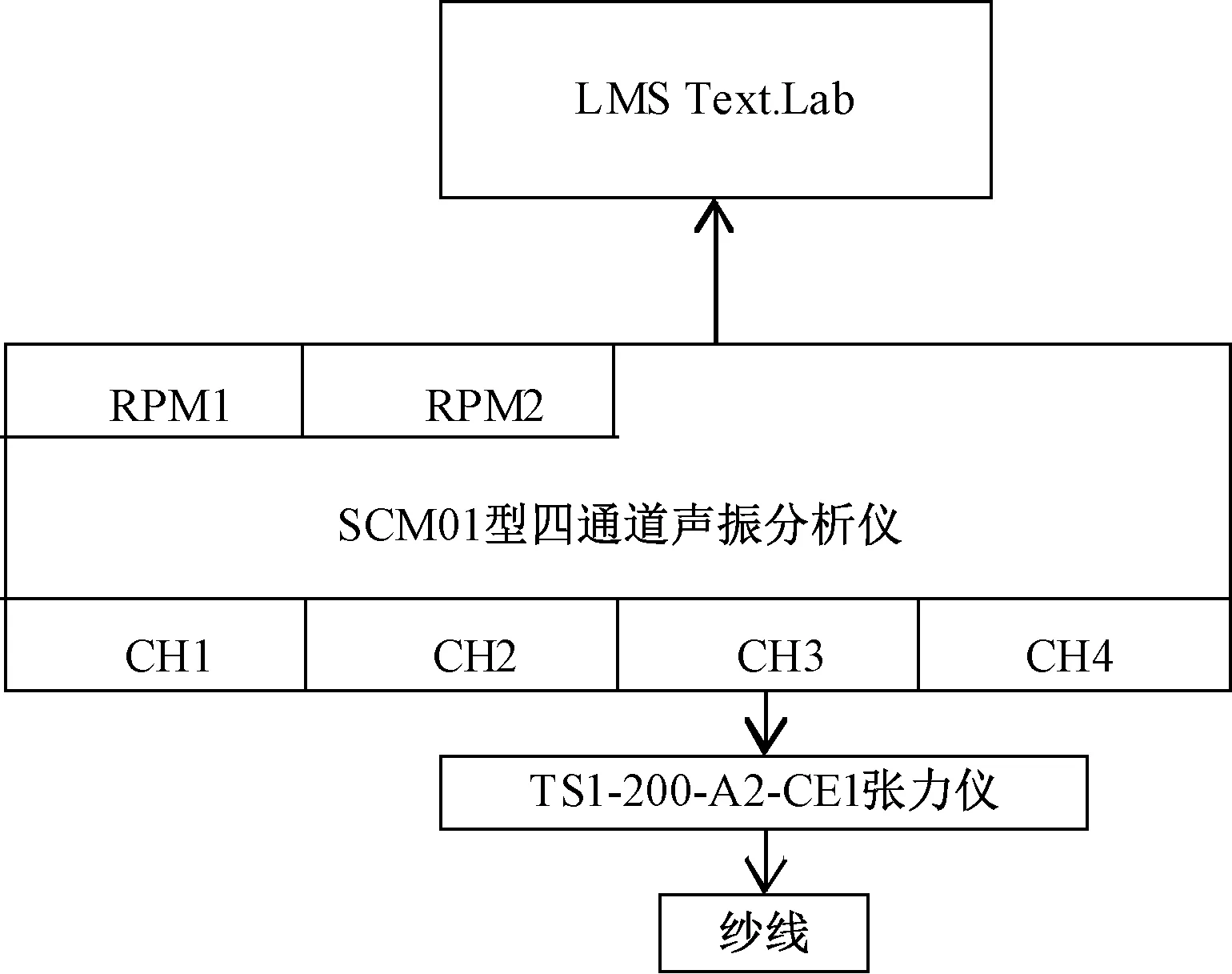
图1 经编纱线张力测试系统Fig.1 Testing system of warp yarn tension
RPM1和RPM2可用于连接主轴编码器,从而获取角度域信号,但本次实验中无需根据角度域信号了解单个周期的张力变化,因此这2个通道暂不使用。CH1、CH2、CH3、CH4这4个通道可任意选择一个连接张力仪。将纱线绕过张力仪上的3个导轮,进行接触式测量。搭建完张力测试系统后,设置采样频率、时间和间隔,本次采样频率为1 kHz,采样时间为30 s,间隔为1 ms。张力仪的张力测试范围为0~2 N,而经编织造时的经纱张力不超过1 N,故远远满足经编纱线张力的测试要求。张力传感器每受到2 N的力产生10 V电压,因此张力传感器的灵敏度设为5 V/N。
2.3 测试工艺参数
采用表1所示的工艺进行上机编织,牵拉密度为28 横列/cm,分别测试5种机速(700、900、1 100、1 300、1 500 r/min)下的纱线张力,对GB1的纱线进行张力测试。测试时车间温度为24.8 ℃,湿度为21%。

表1 测试工艺参数Tab. 1 Test parameters
2.4 测试结果分析
此次采样频率为1 kHz,采样时间为30 s。当机速为1 500 r/min时,在采样时间下一共采集750个成圈过程,共385 024个数据,即每个成圈过程采集约513个数据。图2示出1 500 r/min机速下纱线张力在部分测试时段的张力曲线图。

图2 机速为1 500 r/min时部分时段张力曲线Fig.2 Temporal tension curve at 1 500 r/min
对30 s内测得的所有张力数据进行统计分析,其结果如表2所示。从表中可以看出:不同机速下的纱线张力均方差基本不变,因此无法用它很好地评价不同机速下的张力波动情况;最大值、最小值、平均值可以用来评价纱线张力整体的大小水平,但表中的最小值、平均值也基本不变,最大值稍有变化,但变化较小,也不能很好地反映不同机速下的张力情况。因此需提出新的评价指标来对纱线张力进行分析比较。
2.4.1概率密度曲线分析
对所得到的30 s内的张力数据进行概率密度分析。根据不同机速下的张力最大值和最小值,可设置统计范围为0.02~0.14 N,以组数来划分,5组数据组数均设置为100组,得到频率分布直方图(见图3)。对直方图进行正态分布曲线拟合,即为概率密度曲线。

表2 不同机速下的张力数据分析结果Tab. 2 Analysis results of tension data at different machine speeds
对比概率密度曲线可看到,不同机速下的曲线呈现出不同的形态特征:机速为700 r/min时,纱线张力在每个组分中的概率密度均较小,组与组之间的概率密度差异小,曲线的波峰低,宽度大,且尾部长度更长,说明张力分布较为分散,张力波动大;随着测试机速的不断提高,张力分布在0.03~0.05 N间的概率密度总和不断增大,曲线波峰越来越高,宽度不断减小,从700 r/min波峰宽度0.03 N减小到1 500 r/min时的0.01 N;当机速为1 500 r/min时,张力分布主要集中在0.03~0.04 N之间,最大概率密度接近0.085,与700 r/min时相差约0.045。波峰高度的增加与宽度的减小,说明不同时段的张力差异更小。此外,随着测试机速的不断增加,频率分布直方图的尾部长度不断减小,从0.12 N不断减小到0.10 N,说明测试机速的增加,使得张力整体分布更加集中,极端值减少。
结合以上曲线特征可得出,随着测试机速的增加,纱线动态张力分布更加均衡,不同时段间的张力差异更小,张力波动减小,张力整体稳定性更好。
2.4.2峰度与偏度分析

图3 不同机速下的纱线张力概率密度曲线Fig.3 Probability density curve of yarn tension at different machine speeds
对采样时间内得到的不同机速下的张力数据进行分析,计算峰度和偏度,结果如表2所示。不同测试机速下的峰度均小于0,说明此次测试中张力分布尾部厚度相对于正态分布要细,极大值附近的值均相对较少。随着测试机速的增加,峰度值从700 r/min时的-0.28一直减小到1 500 r/min时的-0.62,减小了121.4%。峰度值不断减小,说明张力分布的尾部厚度变细,极端值更少。从偏度来看,5种机速下的数据偏度均大于0,说明这些机速下张力分布的右侧尾部要比左侧长,呈现右偏的状态,说明张力极大值附近的数值相对于极小值附近的数值更少,张力主要在较小的水平波动,偶尔出现较大张力。比较不同测试机速下的张力偏度可以看到,随着测试机速的增加,偏度值不断减小,从700 r/min时的0.99减小到1 500 r/min时的0.91,减小了8.1%,说明张力分布的右侧尾部是不断缩短的。从峰度和偏度的分析可得出,测试机速增加,张力极端值减少,张力分布更集中,张力波动更小,结果与概率密度曲线分析一致。
2.4.3结果验证
根据实际织造速度,选取机速从1 500 r/min开始不断递减到700 r/min。在1 500 r/min时,机器可稳定顺利织造,坯布疵点少。随着机速的下降,在测试过程中,成圈机件的配合声音增大,纱线整体晃动幅度增加,张力杆抖动增加,说明纱线动态张力随测试机速下降,波动不断增大,这与概率密度曲线和峰度、偏度分析结果一致,从而验证以上评价指标的可行性。概率密度曲线和峰度、偏度可用来分析比较纱线动态张力的波动情况。
3 结 论
本文提出了一种用于评价经编纱线动态张力整体波动情况的评价指标,即概率密度曲线、峰度、偏度值。概率密度曲线可对纱线张力进行一个定性的分析,可展示纱线动态张力的具体分布状态及分布概率;而峰度、偏度可对纱线动态张力进行定量的分析比较,可从数据的大小直接比较出不同情况下的张力波动情况。结合概率密度曲线和峰度、偏度可对高频张力测试系统下得到的纱线动态张力进行比较分析,了解不同情况下的张力波动情况。
通过实验验证了利用概率密度曲线和峰度、偏度评价不同机速下经编纱线动态张力整体波动情况的可行性。不同机速下张力峰度均小于0,偏度均大于0,且随着测试机速的增加,张力峰度和偏度值不断减小,结合概率密度曲线,得出测试机速增大,张力分布更加集中,张力整体波动不断减小,与实际生产情况一致。
FZXB
[1] LIU Xing, MIAO Xuhong. Analysis of yarn tension based on yarn demand variation on a tricot knitting machine[J]. Textile Research Journal, 2016,87(4):487-497.
[2] 冯勋伟. 经编机经纱张力分析及合理上机条件探讨[J]. 纺织学报,1989,10(7):25-28.
FENG Xunwei. Investigation on reasonable working condition and warp tension analysing of warp knitting machine[J]. Journal of Textile Research, 1989, 10(7):25-28.
[3] 刘苏. 经编电子送经系统的动态响应特性[D]. 无锡:江南大学,2013:32-37.
LIU Su.Dynamic response characteristics of the warp electronic let-off system[D]. Wuxi: Jiangnan University,2013:32-37.
[4] MIKOLAJCZYK Z. Modeling of the knitting process with respect to the optimisation of the construction parameters of warp-knitting machines[J].Fibres and Textiles in Eastern Europe,2009,17(73):76-81.
[5] 陈红霞,蒋高明. 经编机经纱动态张力数字化测试[J]. 针织工业,2004,12(6):35-38.
CHEN Hongxia, JIANG Gaoming. Digital testing of the dynamic tension of warp yarns on warp knitting machines[J]. Knitting Industries,2004,12(6):35-38.
[6] 戴斌. 随机振动的特征表述和测量[J]. 中国测试技术,2004,30(6):43-44.
DAI Bin. Random vibration′s character and measuring[J]. China Measurement Technology,2004,30(6):43-44.
[7] 李德昭,王贤洁,沈蓉芬. 数据分析技术在纺织上的应用:纺纱张力的相关分析[J]. 纺织学报,1980,1(6):47-55,79.
LI Dezhao, WANG Xianjie, SHEN Rongfen. An application of data analysis technique to textile research correlation study of spinning tensions[J]. Journal of Textile Research, 1980,1(6):47-55,79.
[8] 田禹. 基于偏度和峰度的正态性检验[D]. 上海:上海交通大学,2012:5-8.
TIAN Yu. Tests for normality based on skewness and kurtosis[D]. Shanghai:Shanghai Jiaotong University, 2012:5-8.
[9] 王学民. 偏度和峰度概念的认识误区[J]. 统计与决策,2008(12):145-146.
WANG Xuemin. Misunderstanding of skewness and kurtosis[J]. Statistics and Decision,2008(12):145-146.
[10] 崔书华,李果,刘军虎,等. 基于偏度与峰度的数据质量评估[J]. 弹箭与制导学报,2015,35(6):98-100,105.
CUI Shuhua, LI Guo, LIU Junhu,et al. Assessment and analysis of trajectory measurement data based on skewness and kurtosis[J]. Journal of Projectiles, Rockets, Missiles and Guidance,2015,35(6):98-100,105.
[11] 杨晓云,岑敏仪,贾洪果. 基于参数统计的LiDAR数据分割算法[J]. 测绘通报,2013(10):20-22.
YANG Xiaoyun, CEN Minyi, JIA Hongguo. LiDAR segmentation based on parameters statistics ana-lysis[J]. Bulletin of Surveying and Mapping,2013(10):20-22.
