平面网格点中无直角的最大点集构造

赵红涛，裴四宝

（华北电力大学数理学院，北京102206）

0 引言

1977年Erdös和Silverman提出这样一个问题：确定最大整数f（n），使得从平面上任意n个点的集合中可以找到f（n）个点，且这些点中任意三个点不会构成一个直角三角形.他们得到对于一个 k×k的网格点中有 f（k2）≤2k－2，Erdös证明了，并且他和Silverman猜想有.1980年H.L.Abbott在文献[1]中证明了Erdös和Silverman的猜想且有，他也指出 Erdös和 Silverman的强猜想 f（k2）＝2k－2是错误的，同时给出了一个反例的定理，即当k≥5时，有f（k2＋k－4）≤2k－3.1995年Gamble B，Pulleyblank W，Reed B等人在文献[2]中探究了从二维平面上的一个给定集合中寻找无直角的最大子集的复杂性，他们证明了这类问题的计算是NP-难的.2009年Gy.Elekes在文献[3]中证明得到.2011年Viktor Harangi，Tamas Keleti等人在文献[4]中研究了多大的Hausdorff维数保证一个给定角.随后，关于点集中不出现直角的研究由欧氏空间转为有限域上的讨论，首先是2015年Michael Bennett在文献[5]中研究了有限域上向量空间中的一些Erdös-Falconer类问题，他证明了在有限域中不含直角的点集的最大基数，在有限域中过原点的任意两个点不构成直角的点集的最大基数.2016年Ge和Shangguan在文献[6]中利用多项式方法对有限域中不含直角的点集的最大基数给出了新的上界，并且得到此最大基数，其中n为有限域的维数，q为素数.

通过Erdös和Silverman对于k×k的网格点中任意三点不构成直角的最大点集的基数为f（k2）≤2k－2的讨论，本文主要研究了m×n网格点中不出现直角的最大点集的基数，通过利用坐标投影法和代数法分别给出了证明，并得到了此最大点集的构造；最后给出了一些关于平面网格点中有待解决的新问题.

1 平面网格点中不出现直角的最大点集

Erdös和Silverman给出：对于平面上n×n的网格点中，不出现直角的最大点集的基数为2n－2.因而，对于在平面上m×n的网格点中，是否会有类似的结果，比如不构成直角三角形的最大点集的基数为m＋n－2.以下本文将用坐标投影法和代数方法分别证明这个结果是正确的.并且令平面上m×n的网格点中不出现直角的最大点集的基数为 f（m，n）.

定理1在平面上的m×n网格点中，f（m，n）＝m＋n－2.

证明：（1）坐标投影法

对于平面上的任意一个m×n网格点，在满足任意三个点不构成直角的条件下，一定能够找到该网格点上大矩形的四个顶点中必有两个点是不能取的，否则它们会出现直角.所以选取这两个空点中任意一个点作为原点，同时以该点所对应大矩形的边为坐标轴作一个平面直角坐标系O－xy，如图1所示.

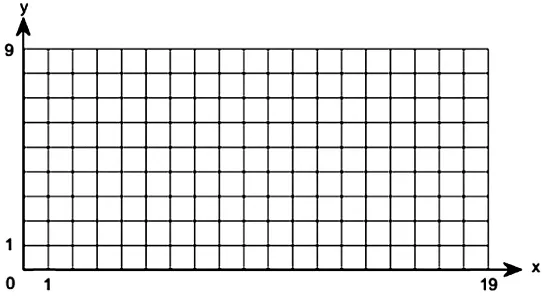
图1 平面上10×20的网格点

为了寻找网格点中无直角的最大点集，应该尽量多的选择使任意三个点不构成直角的点，对于这类构造得到的点集，可以分三种情形：1）点在x轴或y轴上；2）两个及两个以上点的横坐标或纵坐标相同；3）其他情形的点.对于这三种类型的点，在使用投影法将这些点投影到坐标轴上的过程中，优先安排第一类点，然后考虑第二类点的投影，最后进行第三类点的投影.

1）点在x轴或y轴上

对于这种类型的点，仍然保持点的位置不变.

2）两个及两个以上点的横坐标或纵坐标相同（不包含坐标轴上的点）

对于这种类型的点，可以将这些点投影到坐标轴上，而不会影响原点集的总个数，这是因为两个及两个以上的点处于同一直线上时，它们有相同的横坐标或者纵坐标，那么就不能再出现与它们纵坐标或者横坐标相同的点.（如图2，两个黑点确定后，白色虚点则不能出现）

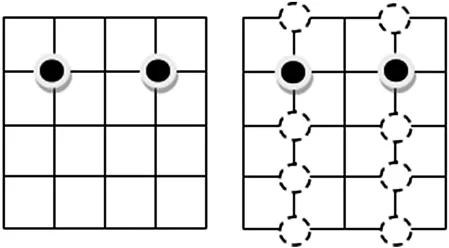
图2 平面网格点中纵坐标相同的点的投影

3）其他情形的点

对于这种情况的点，要么是非坐标轴上的单个点，要么点与点之间是处于对角的情形，这类点可以将其投影在前两类点投影后的坐标轴仍为空点处的位置，并且它不会影响点集总数的变化，这里要求任意一个点不与其他任一点处于同一条直线，否则属于第二种情形考虑.点集投影示例如图3（其中，黑点表示未投影或投影后点的位置，白色虚点表示投影前点的位置）.

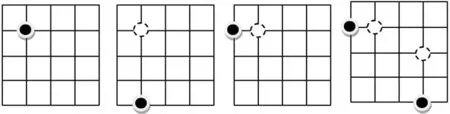
图3 平面网格点中单个点与对角点的投影

由于满足条件的点都可以通过以上三种情形进行投影，在规定的顺序下最后可以将所有点投影到x轴和y轴上，并使每个点都不重复投影，投影后所得到的点数最多的情形如图4.

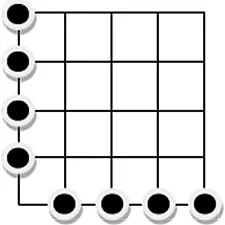
图4 平面网格点中投影后所得到的点数最多的情形

显然，这样所构造的点都不能构成直角三角形，并且图4中的点集情形就是平面上m×n网格点中不出现直角的最大点集，又由坐标轴上的点总数为m＋n－1，而原点为空点，因此有 f（m，n）＝m＋n－2.

（2）代数法

由图1可知，建立坐标系O－xy后，m×n网格点就是横坐标介于0和n－1之间，纵坐标介于0和m－1之间的整点构成的网格点.那么假设，即 P 表示平面上m×n网格点中不出现直角的最大点集；

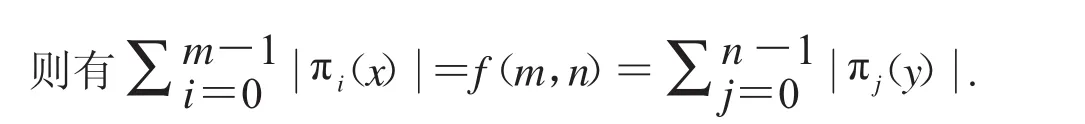
Px＝，Px表示该网格点中满足条件且每行点集的点数大于1的所有点集；

Py＝，Py表示该网格点中满足条件且每列点集的点数大于1的所有点集；

显然有 Px∩Py＝Ø，

当 m＝2或n＝2时，m×n网格点中的最大点集的基数为f（m，n）＝n或f（m，n）＝m.

当m≠2且n≠2时，m×n网格点中的每行或每列的单点个数必小于等于m－1或n－1，否则f（m，n）不是网格点中的最大点集的基数，与假设矛盾.

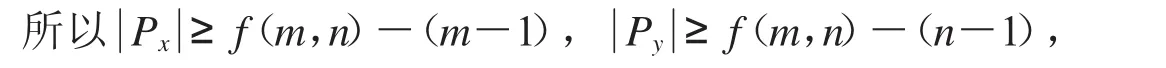
因此有，2f（m，n）－m－n＋2≤f（m，n），则有 f（m，n）≤m＋n－2.

综上所述，f（m，n）＝m＋n－2.

2 结论与展望

本文主要是对二维平面网格点中不出现直角的最大点集进行讨论，得到了平面上m×n网格点中不出现直角的最大点集的基数为m＋n－2，并分别给出坐标投影法与代数法的两种证明；另外，如果将网格点中任意三个点不构成直角的问题转化为网格点中过原点而不构成直角的问题，那么对于n×n网格点与m×n网格点中过原点而无直角的最大点集的基数分别是多少呢？这也是我们下一步将要研究的内容.

[1]ABBOTT H L.On a conjecture ofErdös and Silverman in combinatorial geometry[J].Journal of Combinatorial Theory，1980，29（3）：380-381.

[2]GAMBLE B，PULLEYBLANK W，REED B，et al.Right angle free subsets in the plane[J].Graphs＆Combinatorics，1995，11（2）：121-129.

[3]ELEKES G.A note on a problem of Erdös on right angles[J].Discrete Mathematics，2009，309（16）：5253-5254.

[4]HARANGI V，KELETI T，KISS G，et al.Howlarge dimension guarantees a given angle?[J].Monatshefte Für Mathematik，2012，171（2）：169-187.

[5]BENNETTM.Extremal results regardingright angles in vector spaces over finite fields[EB/OL].[2017-03-23].https://arxiv.org/pdf/1511.08942.pdf.

[6]GE G，SHANGGUAN C.Rank counting and maximum subsets ofcontaining no right angles[EB/OL].[2017-03-23].https://arxiv.org/abs/1612.08255.