基于序贯分析的制导弹药命中精度试验一次抽样方案
2018-03-12李阿楠廖学军
李阿楠,廖学军
(1.解放军装备学院,北京 101416;2.武警后勤学院军交运输系,天津 300301)
0 引言
制导弹药命中精度主要由两部分组成,即命中准确度和命中密集度,系统误差是影响准确度的主要因素,而随机误差是影响密集度的主要因素[1]。在制导弹药命中精度试验中,人们常采用圆概率偏差(CEP)假设检验方法进行试验,试验方案一般采用一次抽样方案或序贯概率比检验方案,并且已制定了相应国标或国军标,如GB/T5080.5-1985、国军标GJB899-97等。一次抽样方案原理简单,试验准备和操作都比较方便,但是不管产品的质量如何,都要经历最多的累计试验数,且有时所需试验样本量过大[2],这对于制导弹药武器来说,试验费用就显得十分昂贵。而序贯概率比检验(SPRT)方案虽能使试验样本量尽可能的少,提高试验效率,但是这种试验方案的累计试验数变化范围较大,有时累计试验数甚至超过一次抽样方案的累计试验数[3]。本文针对这两种试验方案的不足之处,提出了基于序贯分析的制导弹药命中精度试验一次抽样方案。
1 制导弹药命中精度试验的一次抽样方案
1.1 制导弹药命中精度的圆概率偏差(CEP)的计算
圆概率偏差(CEP)指的是以瞄准点为圆心,包含弹着点50%的圆的半径R[4-5]。 在制导弹药落点精度试验中,最常见的是采用圆概率偏差(CEP)的假设检验方法。即:
H0:CEP=CEP0,H1:CEP=λCEP0
式中,λ为检出比,λ>1,由生产方和使用方协商确定。
设对平面目标进行射击,以瞄准点为原点,以射击方向为纵轴,垂直射击方向为横轴,落点坐标为(x,z),且(x,z)服从正态分布,纵横向独立,(x,z)~N(ux,uz,σx,σz),此时(CEP)的计算如下[6-7]:
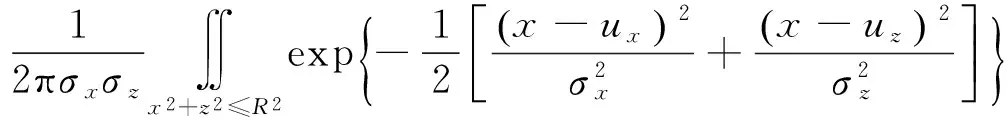
(1)
当p=50%,R即为所求的CEP的值。需要指出的是,在做命中精度试验时,通常先评估系统性误差,即(ux,uz),然后对系统性误差进行补偿,使其降到最小,最终使射弹散布中心与瞄准点重合,这也是武器系统在总体设计时提出的战术技术要求[1]。因此,CEP的计算可进一步简化如下式:
(2)
设σx=σz=σ,进一步转换成极坐标进行求解得:
(3)
进一步简化得:
(4)
(5)
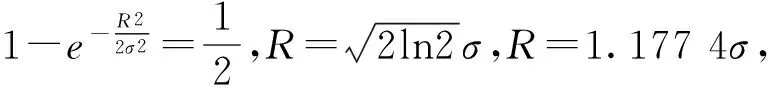
同理,不同的p可以得到不同的以R为半径的圆。

1.2 制导弹药命中精度试验的一次抽样方案设计
根据圆概率偏差(CEP)的概念,在制导弹药精度试验中,如果有50%以上的制导弹药落在了以CEP为半径的概率圆内,则证明该型制导弹药的命中精度达到了设计要求。同理,如果有85%以上的制导弹药落在了当p为85%时的概率圆内,则也证明该型制导弹药的命中精度达到了设计要求[8]。在靶场试验时,最常用的试验方案为一次抽样方案,下面举例说明一次抽样方案的设计。
由图2和图3可知,实验残差分布在常态范围内,实验选取的模型合适;实验值与预测值吻合良好,实验值基本上平均分布于预测线周围。响应曲面设计(BBD)的实验模型能够很好地反映微波干燥草果过程中自变量与响应值之间的实际规律。
1)设某制导弹药的命中概率设计指标为85%,σx=σz=σ=50 m,根据使用方和生产方共同协商确定“弃真”和“采伪”的概率值,即α和β的值,α=0.3,β=0.3,要求设计该型制导弹药命中精度试验的一次抽样方案。
2)由于制导弹药的命中概率为0.85,所以根据概率圆的定义,首先计算p为85%时的概率圆半径R,根据公式(5)来计算。
R=1.9478σ=1.9478×50=97.39 m
以瞄准点为圆心,R=97.39 m为半径画圆,制导弹药落点在此圆内为成功,不在此圆内为失败。
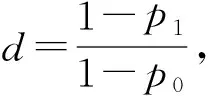
求解以上方程组,得出N和AC的值,由于N和AC均为整数,所以N和AC的最终结果为α和β值最接近要求值时所求解出来的整数。靶场一般是根据现成的国标或国军标,查表得到N和AC的值,本文使用Matlab语言进行编程求解,表1为所求结果,其中α′、β′ 为生产方和使用方实际的“弃真”和“采伪”的概率,这在现有的国标和国军标上是查不到的。
根据表1计算的结果,综合考虑制导弹药的价格和试验费用及“弃真”和“采伪”的概率大小等因素,来确定发射制导弹药的总发数和允许失败的发数。在本例中,可取N=16,AC=3。也就是说,在发射的16发制导弹药中,如果最多有3发弹没有落在以半径为R=97.39 m的概率圆内,则表明该型制导弹药的命中精度符合设计指标要求。如果有4发或4发以上弹失败,则表明该型制导弹药的命中精度不符合设计指标要求,这就是经典的一次抽样试验方案。

表1 制导弹药命中精度试验一次抽样方案
2 基于序贯分析的一次抽样试验方案
在一次抽样方案中,有时所需样本量较大,如在上例中,其他条件不变,只是将制导弹药命中精度改为95%,那么N=36,AC=3。由于制导弹药的造价一般都比较昂贵,试验费用比较高,尤其是战略制导弹药,不可能提供大量的试验用弹[9-10]。因此在保证试验精度的基础上,一般都希望试验用弹量越少越好。本文提出了一种基于序贯分析的一次抽样试验方案,该方案是在一次抽样方案的基础上进行序贯试验,有效地减少了试验用弹量,提高了试验效率。下面结合上例说明基于序贯分析一次抽样试验方案的设计步骤。
1)在上例中,根据一次抽样方案的计算结果,总发射弹数为16发,允许失败弹数为3发,因此我们可以计算发射数从4发开始到12发所占总发射数的百分比及所对应的概率圆半径[11],计算结果如表2所示。
根据圆概率偏差的概念,结合表2的计算结果,我们可得出以下结论,如果有4发弹落在了以R4为半径的概率圆内,则证明该型制导弹药的命中精度符合设计要求,则可以停止发射,结束试验。如果没有,则继续发射,直到发射弹数落在了所对应的概率圆内,则试验结束[12],这就是序贯分析。

表2 发射弹数占总数的百分比及概率圆半径
2)但是上述序贯试验方法的“弃真”和“采伪”的概率有多大呢?生产方和使用方可以接受吗?因此,我们计算了这种序贯试验方法的“弃真”和“采伪”的概率值,如表3所示。

表3 采用序贯分析方法所对应的α′和β′的值(λ=1.5)
从表3可以看出,“弃真”α′的概率值较大,不能满足生产方的要求,所以这个方法必须进行改进。
3)为了调整实际的“弃真”和“采伪”的大小,我们根据公式(5),通过调整发射弹数所对应的概率圆半径的大小,从而改变命中率p0大小的方法,最终改变α′、β′的大小。计算结果如表4所示。
通过表4我们可以看出,通过调整发射弹数所对应的概率圆半径的大小,使得α′的值有所减小,从发射第5发弹开始,α′<0.3、β′<0.3,满足了生产方和使用方的要求。
结合本例,基于序贯分析的一次抽样方案总结如下:首先计算总发射弹数为16发,最多允许3发弹发射失败,即3发弹落在了以R=97.39 m为半径的圆外,当有4发弹发射失败时,则可判定该型制导弹药命中精度达不到指标要求,实验结束;如果失败弹数不超过3发,则继续发射,然后检查发射弹数是否落在所对应(调整后)的概率圆内(表4),如5发弹落在R=46.4 m的概率圆内,或6发弹落在了R=52.2 m的概率圆内,以此类推,若是,则判定该型制导弹药命中精度达到指标要求,试验结束。

表4 调整概率圆后所对应的α′和β′的值(λ=1.5)
3 结论
本文提出了基于序贯分析的制导弹药命中精度试验一次抽样方案。该方案将两种试验方案的优点结合了起来,试验前便可知试验样本数,便于靶场和生产方进行试验准备,试验中根据序贯分析,随时做出“接受”和“弃收”的决定。实例证明,该试验方案在保证试验精度的同时,能有效减少累计试验数,节约了试验费用,提高了试验效率。
[1]张金槐.地-地制导弹药落点的精度和密集度的统计评定[J].国防科技大学学报,1987,20(1):20-30.
[2]GB/T 5080.5-1985 设备可靠性试验成功率的验证试验方案[S].北京:航天工业部708所,1985.
[3]王正明,卢芳云.制导弹药试验的设计与评估[M].北京:科学出版社,2010:59-61.
[4]金忠.圆概率偏差的测定与检验[J].南京理工大学学报,1995,19(2):135-138.
[5]朱向明,周凤岐.防空导弹引信飞行试验故障模式影响分析[J].探测与控制学报,2009,31(3):39-42.
[6]张金槐.小子样下命中概率的估计[J]. 国防科技大学学报,2001,23(6):109-113.
[7]唐雪梅,李荣,等.武器装备综合试验与评估[M].北京:国防工业出版社,2013:100-108.
[8]李延杰.导弹武器系统的效能及分析[M].北京:国防工业出版社,2000:101-108.
[9]纪永祥,刘社锋.对空近炸引信试验与结果评定方法研究[J].探测与控制学报,2006,28(6):14-16.
[10] 金星,洪延姬,等.导弹飞行试验命中精度验证一次抽样方案快速确定方法[J].装备学院学报,2002(4):4-26.
[11]程光显,张士峰.导弹落点精度的鉴定方法—概率圆法[J]. 国防科技大学学报,2001,23(5):13-16.
[12]唐雪梅,蔡洪,杨华波,等.导弹武器精度分析与评估[M].北京:国防工业出版社,2015:251-253.
