基于矢量修正的稀疏阵列测向解模糊方法
2018-03-12韩佳辉毕大平
韩佳辉,毕大平,陈 璐
(国防科技大学电子对抗学院,安徽 合肥 230037)
0 引言
波达方向(Direction of Arrival,DOA)估计是雷达对抗领域的核心研究内容之一,对获取战场主动性,争夺制信息权具有重要的作用。现代电磁环境中,信源密集且复杂多变,往往需要对多信源精确测向,传统测向体制难以完成使命。超分辨阵列测向技术能够同时精确估计多个信号的方位,克服了传统测向体制的缺陷。MUSIC(Multiple Signal Classification)[1]算法作为一种最经典的超分辨算法,自提出以来有很多学者对它进行了大量的改进[2-4],但是目前的优化算法大多数是针对阵元间距小于半波长的均匀线阵(ULA)设计的,存在着阵列孔径小、测向精度低和分辨率差等缺点,难以适应现代战场电磁环境。稀疏阵列是指阵元间距大于半波长的阵列系统,相比于相同阵元数目的常规满秩阵列,稀疏阵列拥有更大的阵列孔径,更大的分辨率,更高的自由度。但是当阵元间距大于半波长时,会出现测向模糊问题。
近年来,已经有很多学者将稀疏阵列引入到DOA估计领域,应用较多的稀疏阵列为嵌套阵和互质阵。文献[5]用 Ziv-Zakai限分析了稀疏线阵测向性能。文献[6]分析了嵌套阵对阵列自由度的提升情况,系统地对阵列进行了虚拟扩展,实现了在阵元数量低于信源数量下的无模糊测向。文献[7]详细推导了嵌套阵阵列结构和可测量信源数目的关系。文献[8]通过多级嵌套阵列,等效地扩展了虚拟阵元的数量,极大地提升了可测信源的数目,避免了测向模糊问题,但是阵列结构复杂,计算量过大。文献[9]设计了一种互质阵列结构,利用阵元间距之间互质的原理,实现了无模糊测向,但是存在阵列形式单一的缺点。然而值得注意的是,现有的稀疏阵列DOA估计算法大都在虚拟阵列扩展的基础上实现测向,存在阵列结构复杂、计算量大、实时性差等缺点,很难满足雷达对抗的作战需求。本文针对以上问题,提出了基于矢量修正的稀疏阵列测向解模糊方法。
1 MUSIC算法数学模型及稀疏阵列模型
1.1 MUSIC算法模型
基于天线阵列协方差矩阵的特征分解类DOA估计算法中,MUSIC算法具有普遍的适用性,只要已知天线阵的布阵形式,无论直线阵还是圆阵,不管阵元是否等间隔分布,都可以得到高分辨的估计结果。设有n个远场窄带不相干的信源以来波方向θk(k=1,2,…,n)入射到阵元数目为m的线阵,设其阵元位置为z=[z1z2…zm],如图1所示。
则整个阵列的接受信号为:
y(t)=A(θ)x(t)+n(t),t=1,2,…,N
(1)
其中,y(t)=[y1(t),y2(t),…,ym(t)]T为阵列的接受数据矢量;x(t)=[x1(t),x2(t),…xn(t)]T为信源矢量;n(t)=[n1(t),n2(t),…,nm(t)]T为均值为0方差为σ2的加性高斯白噪声列矢量;A(θ)=[a(θ1),a(θ2),…,a(θn)]为阵列流形矩阵,a(θk)=[ejωkz1,ejωkz2,…,ejωkzm]T为第k个信号的导向矢量,其中ωk=2πsinθk/λ为第k个信号单位距离的相位差;N为快拍数。阵列协方差矩阵为:
Ry=E[y(t)yH(t)]=ARxAH+σ2I
(2)
其中,Rx=E[x(t)xH(t)]表示入射信号矢量的自相关矩阵,将Ry分解为信号子空间US和噪声子空间UN,A和US相同且和UN正交。定义阵列空间谱函数为:
(3)
由上式,使θ变化,通过寻找波峰来估计到达角。
1.2 稀疏阵列
为了便于分析,假设信源半波长λ/2=1,若以第一个阵元为参考阵元,则阵元数目为m,阵元间距d=λ/2的均匀线阵可以表示为z=[0 1 2 … (m-1)]。由于稀疏阵列阵元间距d>λ/2,那么阵元数目为m,阵元间距d=M均匀稀疏阵列可以表示为:
其中,M>1且M∈N。
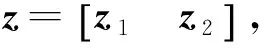

图3 互质阵列(●阵列 1,○阵列 2)
Fig.3 Coprime array (●array 1, ○array 2)
2 稀疏阵列无模糊测向方法
若阵列阵元个数为m,只有对于任意n+1个单位距离相位差ωi(0≤ωi<2π,1≤i≤n+1),扩展阵列流形Aaug=[a(ω1)a(ω2) …a(ωn)a(ωn+1)]的秩满足rank(Aaug)=n+1时,MUSIC算法可以无模糊估计出n(n 定义g=gcd(z2,z3,…,zm),其中gcd为最大公约数运算符。为便于分析,假设信源半波长λ/2=1,则单位距离相位差可以表示为ω=2πsinθ/λ=πsinθ,若来波方向θ∈[-π/2,π/2),则ω∈[-π,π)。 1) 阵元相对位置最大公约数等于信源半波长,即g=1。 (4) (5) (6) (7) 所以 (8) 因为gcd(z2,z3,…,zm)=g,上式可以写成 (9) 2) 阵元相对位置最大公约数大于信源半波长,即g>1。此时导向矢量可以表示为: (10) (11) 若在稀疏ULA位置为N处添加一个阵元,此时阵列表示为zC=[zM|N]如图4所示,即 (12) (13) 图4 稀疏均匀线阵增加阵元(gcd(M,N)=1) (14) 若aM(ω1)=aM(ωn+1),那么 (15) c1+cn+1=0,c2=c3=…=cn=0 (16) 式(14)最后一行为: c1ejNω1+c2ejNω2+…+cn+1ejNωn+1=0 (17) 将式(16)代入到式(17)中,得 ejNω1=ejNωn+1 (18) 这就意味着当-π/2≤ω1<ωn+1<π/2时,ωn+1-ω1=2πl/N,1≤l M/N=k/l (19) 本节通过仿真实验首先验证阵列相对位置的最大公约数与测向模糊之间的关系;然后验证所提方法解稀疏阵测向模糊的有效性;最后通过与阵元间距为半波长的阵列测向性能相比,验证所提方法的性能。 实验1 阵元相对位置的最大公约数与测向模糊关系 采用非等间距稀疏线阵,阵元数目m=7。两远场不相干信源分别以θ1=-30°,θ2=40°两个角度入射。信噪比SNR=0 dB,快拍数1 000。图5由(a)到(d)为阵元相对位置最大公约数与信源半波长比值分别为g/(λ/2)=1,g/(λ/2)=2,g/(λ/2)=3,g/(λ/2)=6,采用MUSIC算法进行DOA估计得到的结果。 实验2 解模糊方法有效性分析 从图6的测向结果可知,对来自于θ1,θ2的两个远场不相干信号,未添加阵元的稀疏ULAz1出现了严重的测向模糊。但增加一个阵元后,阵列z2极大的抑制了虚假谱峰,基本实现了测向解模糊。可见,所提方法能够有效地解决稀疏阵列的模糊问题,并且阵列形式更加灵活,有利于工程实现。 实验3 DOA估计性能比较 从图7(a)和图7(b)可知,当5个信源入射时,半波长均匀阵列已经不能有效的分辨出信号的个数。而本文方法仍能够分辨多个入射信号,具有更好的多目标分辨能力。从图7(c)和图7(d)可知,当2个信源以θ2=(30°,32°)入射时,角度差为2°时,半波长均匀阵列因为信源角度差较小,不能准确估计信源入射角,测向精度较低。而本文方法保留了稀疏阵列孔径大的特点,准确估计出信源入射角,具有更高的测向精度。 实验4 DOA估计性能统计分析 采用与上一节相同的阵列。一远场信源以θ=30°入射到两阵列上。均方根误差 (20) 式中,L代表蒙特卡洛实验的次数,进行300次蒙特卡洛实验,可得到如图8所示结果。 从图8(a)可知,在低信噪比条件下,半波长均匀阵列的均方根误差较大,测向精度显著下降。而本文方法在低信噪比条件下,仍能准确实现DOA估计。当信噪比较高时,本文方法比传统的阵元间距为半波长的阵列DOA估计精度更高。从图8(b)可知,所提方法本文所提方法在快拍数域全面优于半波长均匀阵列。 本文提出了基于矢量修正的稀疏阵列测向解模糊方法。该方法通过推导阵元相对位置与稀疏阵列角度估计之间的关系,分析了阵元相对位置的最大公约数对MUSIC算法测向性能的影响,利用在稀疏均匀线阵特定位置添加新的阵元的方法,对原阵列的导向矢量进行修正,解决了稀疏阵列的测向模糊的问题。仿真实验结果表明,该方法不仅保留了稀疏阵大孔径的优点,提高了多信号分辨能力和测向精度,并且在低信噪比和小快拍条件下性能较好。 [1]Schmidt R O. Multiple emitter location and signal parameter esti-mation[J]. IEEE Trans. Antennas and Prop, 1986, 34(3):276-280. [2]Cheng Qian, Lei Huang. Improved unitary root-MUSIC for DOA estimation based on pseudo-noise resampling[J]. IEEE Signal Processing Letters, 2014, 21(2):140-144. [3]Pascal Vallet, Xavier Mestre, Philippe Loubaton. Performance analysis of an improved MUSIC DOA estimator[J]. IEEE Trans on Signal Processing, 2015, 63(23):6407-6422. [4]Low-complexity DOA estimation based on compressed MUSIC and its performance analysis[J]. IEEE Trans on Signal Processing, 2013, 61(8):1915-1930. [5]Khan D, Bell K L. Analysis of DOA estimation performance of sparse linear arrays using the Ziv-Zakai bound[J]. IEEE Radar Conference, 2010:746-751. [6]Pal P, Vaidyanathan P P. Nested arrays: a novel approach to array processing with enhanced degrees of freedom[J]. IEEE Trans. on Signal Processing, 2010, 58(8): 4167-4181. [7]Keyong Han Arye Nehorai. Improved source number detection and direction estimation with nested arrays and ULAs using jackknifing[J]. IEEE Trans on Signal Processing, 2013, 61(26): 6118-6128. [8]Keyong Han Arye Nehorai. Nested array processing for distributed sources[J]. IEEE Signal Processing Letters, 2014, 21(7):1111-1114. [9]Si Qin, Yimin D Zhang. Generalized coprime array configurations for direction-of-arrival estimation[J].IEEE Trans on Signal Processing,2015,63(6):1377-1390. [10]Elie BouDaher, YongJia. Multi-frequency co-prime arrays for high-resolution direction-of-arrival estimation[J]. IEEE Trans on Signal Processing, 2015, 63(5):3797-3808. [11]Stoica P, Nehorai A. MUSIC, maximum likelihood, and Cramer-Rao bound[J]. ICASSP, 1988, 21(4): 2296-2299. [12]Manikas A. Differential geometry in array processing[M]. London: Imperial CollegePress, 2004. [13]郭跃,王宏远,周陬.阵元间距对MUSIC算法的影响[J].电子学报, 2007, 35(9):1675-1679.2.1 阵元相对位置最大公约数对测向性能的影响
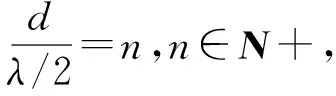
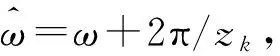

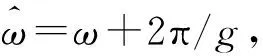
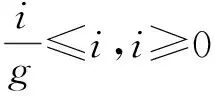
2.2 导向矢量修正解模糊方法
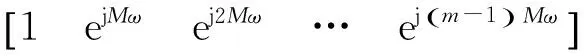


Fig.4 Spare ULA with another element (gcd(M,N)=1)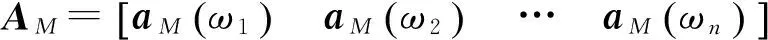
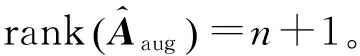
3 仿真实验
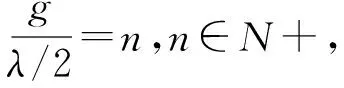
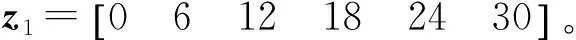
4 结论
