关注起点 深度加工 认知建构——以“按比例分配解决实际问题”为例

江苏江阴市辅延中心小学 沈 莉 金 雯

“比的应用——按比例分配”是苏教版小学数学教材六年级第十一册第三单元的最后一个内容。这部分内容含一个例题，安排1个课时进行教学，例11主要教学按比例分配的实际问题。

按比例分配问题大致有三种解法：教材采用把比转化成分数，使之成为分数乘法应用题，接着求一个数的几分之几是多少，也采用把比转化成分数后，把题目化为归一应用题。而作为正比例的习题，更能体现按比例分配的本意。解决问题中数量之间的比例关系，到第十二册学习正比例之后，才能引导学生加以认识。教学按比例分配这部分内容时，不论采用哪一种解法，必须根据比的意义弄清把总量分成几份，每个部分数量各占总数的几分之几或每份是多少，然后选择适当的方法进行解答。

以下是笔者三轮“按比例分配解决实际问题”的教学，以关注学生为起点，逐渐走向深度加工，最后落脚于知识结构化。

一、第一轮：关注学生认知起点

本节内容是学生在学完比的意义、比的基本性质后进行的，主要引导应用比的意义解答有关按比例分配的实际问题。学生在学习的过程中进一步体会数学知识间的内在联系，建立合理的认知结构。本节内容是平均分的延伸，与分数乘法有密切联系，也是学习第十二册教材比例知识的基础。

按照教参建议，按部就班，第一步理解题意，要求学生弄清题意是把30个方格按1∶2∶3的比例进行分配；第二步自主探索，引导学生独立思考或交流不同解决问题的方法，并选择一种自己喜欢的方法算出结果，再进行检验；第三步拓展认识，教师提出“把30个方格按1∶2∶3涂成红、黄、绿三种颜色，求三种颜色各应涂多少格”这一问题后，学生列式解答，并组织交流；最后引导学生比较例11中两个问题的解题过程，说一说它们有什么相同的地方，帮助进一步明确按比例分配问题的解题过程。

教学很顺利，学生学得也很轻松，可教学结束后的作业结果反馈却让教师大跌眼镜。稍变化的题目没有抓手，学生表现出很懵懂的状态。这是为什么呢？

毫无疑问，一切学习都建立在学生已有认知基础上。奥苏伯尔说：“影响学习的最重要的原因是学生已经知道了什么，我们应该根据学生原有的知识状态进行教学影响。”可由于每个人在生活经验、知识基础、学习能力、思维品质、个人素养等方面存在差异，不同学生已有的认知基础是不一样的，即便他们经历了同样的学习过程。这其中不仅对应着学生的认知起点，更隐藏着学生发展可能性的秘密。

二、第二轮：深度加工所学知识

《义务教育数学课程标准（2011年版）》指出：学生的数学学习不仅要考虑数学自身的特点，更应遵循学生学习数学的心理规律，让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程。选择一种你喜欢的方法解答后，我们发现，不管是学优生还是学困生，多数都选择转化为归一应用题的解决方法解答。归一解答，先计算出每一份是多少，方法比较简便，便于知识迁移到解答一些稍有变化的题目中去。

鉴于第一轮的教学经验，我们做好题目的整理序编，展开了3个课时的教学工作。

（一）简单的按比例分配问题

（1）一根长4.8米的绳子按3∶2截成甲、乙两段，甲、乙两段各长多少米？

（2）一根绳子按3∶2截成甲、乙两段，已知甲段长4.8米，乙段长多少米？

（3）一根绳子按3∶2截成甲、乙两段，已知乙段比甲段短4.8米，甲、乙两段各长多少米？

（二）稍复杂的按比例分配问题

1.根据部分量的比找准对应的总量和

（1）一个长方形的周长是360厘米，长与宽的比是4∶2，这个长方形的长和宽各是多少？

（2）三个人的平均年龄是40岁，这三个人年龄的比是2∶5∶3，最小的年龄是多少岁？

（3）长方体的长、宽、高的比是5∶3∶1，棱长之和是144米，这个长方体的体积是多少立方米？

（4）在一道减法算式中，被减数、减数与差的和是270，差与减数的比是2∶7，这道减法算式中减数是多少？

2.根据总量补全相对应的比

（1）一个等腰三角形，两个角的比是1∶2，这个三角形可能是什么三角形？

（2）一个等腰三角形，两条边的比是1∶2，这个三角形是什么三角形？

3.根据总量理解相对应的比

（1）两个城市相距360米，货车和客车同时从两城市相对开出，经过3小时相遇。货车和客车的速度比是7∶5。货车和客车各行多少千米？

（2）两个城市相距360米，货车和客车同时从两城市相对开出，经过3小时相遇。货车和客车的路程比是7：5。货车和客车每小时各行多少千米？

4.根据比找准相对应的量

（1）把一批图书按4：5：6分借给二、三、四三个班，已知二班比四班少分得48本。三个班各分得多少本？

（3）玩具厂有两个车间，甲车间和乙车间的人数比是3∶2，若从甲车间调走24人到乙车间，两车间的人数恰好相等，这个玩具厂共有多少工人？

（三）复杂的按比例分配问题（找到公共量和不变量）

（1）甲、乙、丙三个班人数的和是420人，甲班和乙班的比是2∶3，乙班和丙班的比是4∶5，甲乙丙三个班各是多少人？

（2）一杯盐水，盐与水的比为1∶5，再加16克盐后，盐与水的比为1∶4，原来盐水有多少千克？

（3）一班和二班的人数比为8∶7，如果将一班的8名同学调到二班去，那么一班和二班的人数的比为4∶5，求原来两个班有多少人？

通过上面的习题配置，我们将学生的无序思维有序化、数学化、系统化，加上辅助性的理解图，正确率明显提高。在做中学知识、做中练技能，总结并内化成学生的一个巩固的规范的分配方法。特别是学困生，也学得特别轻松，有了成功的体验和收获。

在教学顺利进行的同时，似乎又有隐隐的不安与疑惑。这节课为什么要安排在分数除法单元中？教师因为已有的知识系统、功力心态、本位思想形成了教学过程中的短视性思维现象。短视性思维局限了教师的思考方式，让教师在目标设定、体系认知、素养落实中缺乏或降低了反思能力。教师应注意突破这种主要由于教学的先后次序所形成的逻辑线索的束缚，并从更为广泛的角度解释这些概念之间的内在联系，从而真正建立起整体性的概念体系。

三、第三轮：力求让知识结构化

数学是整体的，其主要表现为数学知识的系统化和结构化。任何数学内容都来自某一系统，从属于某一结构。从结构的角度来把握所学习的数学内容，不仅能凸显内容的实质，建立内容直接的联系，而且有利于学生形成 “从结构的角度把握事物本质”的结构化思维。每一节课的教学都应积淀为上一个台阶，成为下一课的起点，不应该有“炒冷饭”的事发生。回归到中年级段的浅表化浅层化，是无法让学生在学习的过程中进一步体会数学知识间的内在联系，建立合理的认知结构的。

师：同学们讨论一下，两种解题方法，有没有相同的地方？又有什么不同的地方？

生：都先根据一定的比求出总的份数。

师：那不同的地方呢？

小结：方法一是求出每份数，再用乘法求几份是多少；方法二是求各部分占总份数的几分之几，再用乘法求总数量的几分之几是多少求出各部分。

随着课程改革的不断深入，尤其是在“四基”“四能”理念的指引下，数学教学已经不再仅仅满足于学生对“双基”的掌握，更要追求学生的可持续发展。有了这样的目标定位，就会多一层关注思维的考虑。课堂上并不仅仅是两种方法的呈现，我们沟通除法与分数的联系，促进认知建构的同时，让学生体会到知识的迁移力与再生力。 读出教材的“联”，从“单一”走向“立体”，学生经历“困惑—思考—交流—领悟”的过程，引导学生跳出知识的点，走向知识的面。

把一根长4.8米的绳子按3：2截成甲、乙两段，甲、乙两段各长多少米？

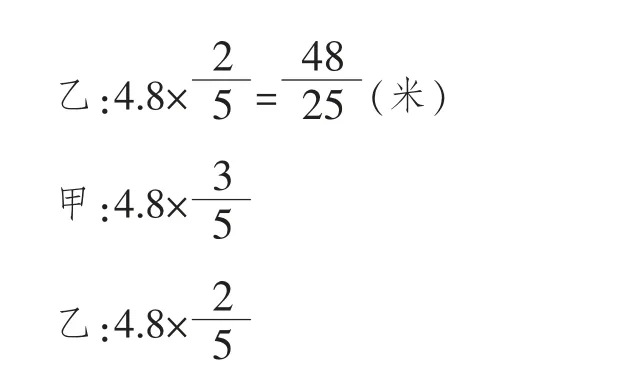
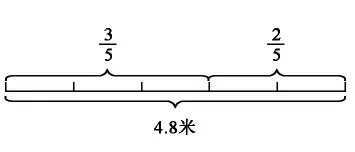
为了实现数学知识在更大范围内的沟通联系，在教学中，教师要帮助学生理清比与分数、份数之间的关系，将它们置于一个框架内，引导学生对已学习过的数学知识进行系统整理，使其形成一些内容比较充实、结构相对完整的数学知识系统，在系统内部实现其内容更高层次上的联系，掌握数学本质。

肖川博士说得好：“教育是一个不完美的人引领着另一个不完美的人追求完美的过程。”数学教师要上好数学课，应该做到三个理解：第一是理解数学；第二是理解学生；第三是理解教学。有了这样的目标定位，就会多一层关注思维的考虑，另一方面也会影响我们在课堂上对学生学习过程的评价方法——不仅仅关注对错，还要关注思维等。教师深度地教，学生深度地学，不断提升课堂教学的品质，丰富课堂教学的思想内涵，真正形成有效的数学活动，才有可能在提升学生的数学核心素养方面逐步获得进展。