带电粒子在电磁场中的运动
2018-03-10朱志平
朱志平
(渭南师范学院数理学院,陕西 渭南714099)
0 引言
带电粒子在电磁场中的运动规律在物理学和科学技术的许多研究领域有着重大意义。就应用而言,质谱仪、示波管、电子显微镜、电视显像管、磁聚焦、粒子加速器等都与它有密切关系。[1]就基础研究而言,人们对原子核和基本粒子的认识大多来源于对其间相互碰撞过程的研究,而带电粒子的碰撞过程则与它们在电磁场中的运动规律密切相关。对于空间物理和天体物理的研究,其研究对象大多是等离子体,其中又存在着各种磁场(如地球磁场、太阳磁场、恒星磁场、星系磁场等),研究带电粒子在这些磁场中的运动对许多现象和过程的认识至关重要。
对于在电磁场中运动的带电粒子,因受库仑(Coulomb)力和洛仑兹(Lorentz)力作用,其运动方程为:


其运动规律比较复杂,难以由理论分析给出一个直观的图像,也不易用实验方法实现。因此,在研究带电粒子在电磁场中的运动规律时,可以借助MATLAB软件功能将带电粒子在电磁场中的运动直观地描绘出来。[2-4]
1 带电粒子在均匀恒定电磁场中的运动
1.1 带电粒子在均匀恒定电场中的运动
带电粒子在电场中,受电场力作用,其运动方程为:

在水平方向(x方向)粒子的运动方程为:
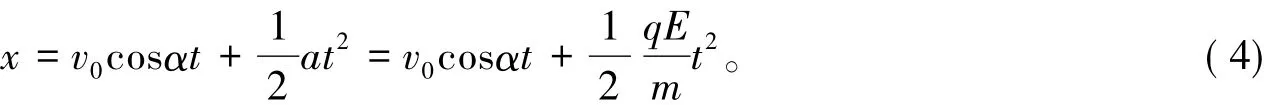
在铅直方向(y方向)粒子的运动方程为:

当α=0或π时,粒子的运动轨迹为:

当α≠0或π时,粒子的运动轨迹为:

取 E=1 N/C,q=1.6 × 10-19C,m=1.6 × 10-19kg=2 m/s,对粒子以不同入射角进入电场进行模拟,模拟图如图1所示。
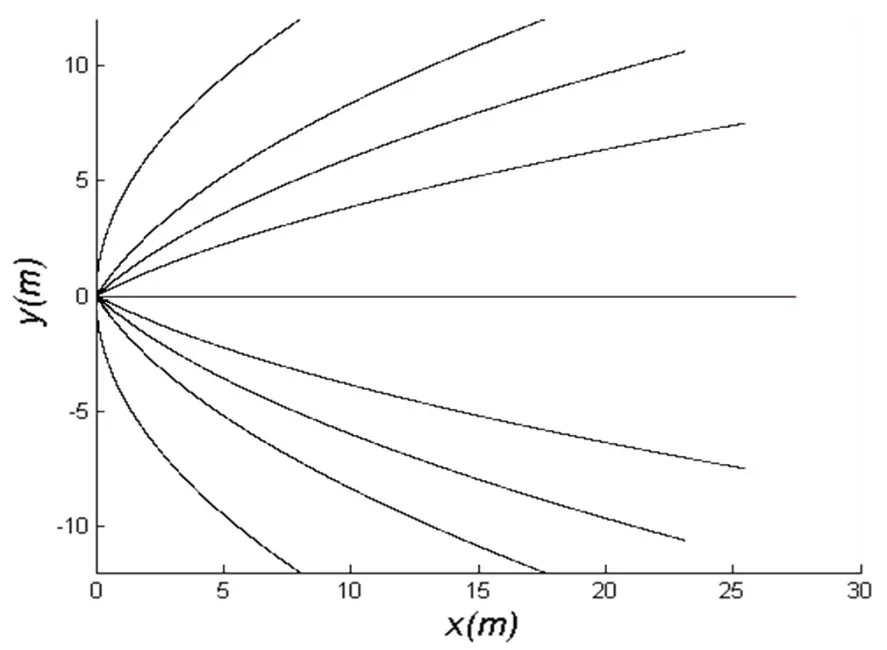
图1 带电粒子在均匀恒定电场中的运动轨迹

图2 带电粒子在匀强磁场中的螺旋运动
1.2 带电粒子在均匀恒定磁场中的运动
1.2.1 带电粒子在均匀恒定磁场中的运动
带电粒子在磁场中运动,受洛仑兹力的作用,其运动方程为:

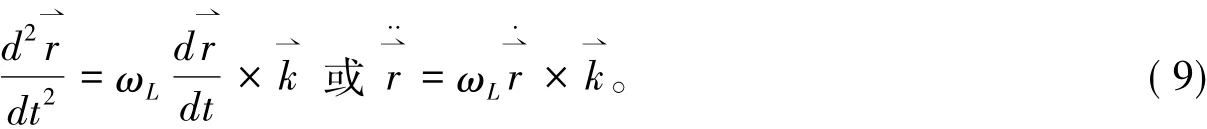
运动方程的分量形式为:

对式(10)求微分并作代换,得

对式(11)积分,得

再积分,得
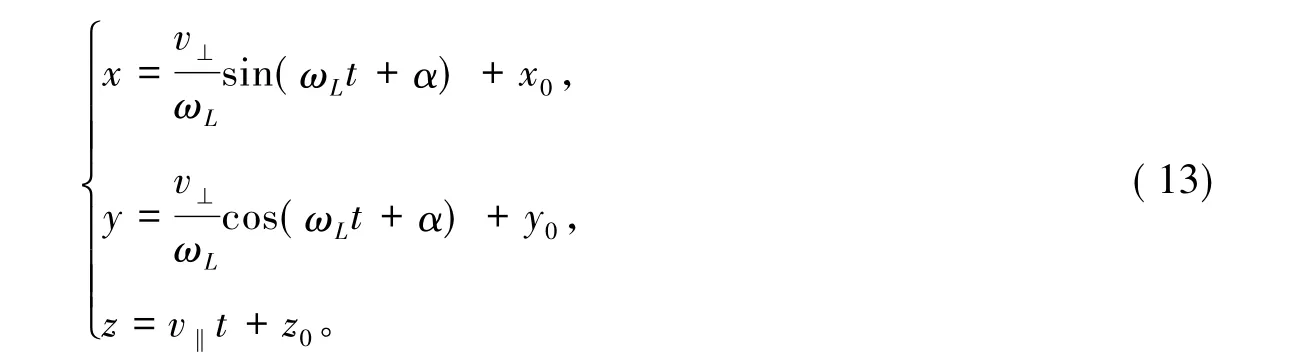
其中:v⊥=v0sinθ,v‖=v0cosθ,α及x0、y0、z0都是由初始条件确定的常数,其中α为初速度在xoy平面内的投影与x轴的夹角。
式(13)表明,带电粒子从初始位置(x0,y0,z0)出发,以初速度的平行磁场分量v‖沿磁场方向作匀速直线运动。同时,在垂直磁场的xoy平面内,以初速度的垂直磁场分量v⊥绕半径为的圆作匀速圆周运动。即x、y、z的表示式(13)式说明此轨迹是一条螺旋线。取初始入射速度方向与z轴成30°夹角进行模拟,模拟图像如图2所示。
1.2.2 磁聚焦原理
运动电荷在磁场中的螺旋运动被广泛地应用于“磁聚焦技术”[3]。磁聚焦在许多电真空系统中得到应用(如电子显微镜)。
由于电子速度的垂直分量各不相同,在磁场力的作用下,电子将沿不同半径的螺旋线前进。[5]但由于水平速度分量近于相等,所有电子从P点经过一个螺距之后又重新汇聚于P'点。这与透镜将光束聚焦成像的作用类似,叫做磁聚焦。
设磁场轴向路径长度为L,一束质量为m、带电量为e的电子先经过较大的轴向电场加速,获得速度v‖;再经过径向交变电压发散,获得不同的但很小的径向速度v⊥;然后进入轴向匀强磁场B中做螺旋运动。电子作螺旋运动的半径为,由于电子带负电荷,利用初始条件:t=0时,x=y=z=0,其运动方程可表示为:

经过1个周期,电子能在端点汇聚,则L/z=1。若L/z=n(n为整数),即增加磁感应强度B而减小周期T,则电子束有n个汇聚点(焦点)。设发散角为θ,则散角越大,焦点越少,则半径越大。如取电子束聚焦3次进行模拟,模拟图如图3所示。
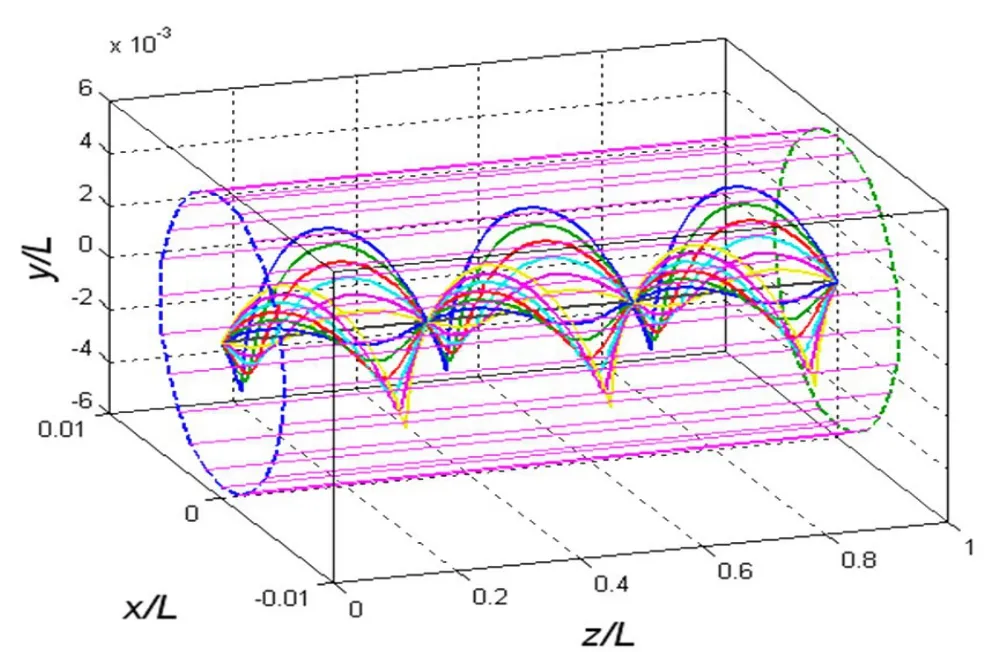
图3 磁聚焦图

图4 空间正交电磁场
1.3 带电粒子在均匀正交电磁场中的运动
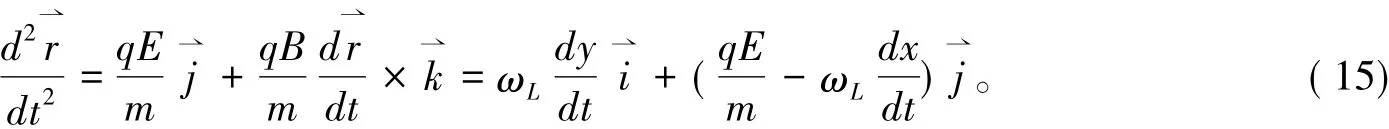
运动方程的分量形式为:

对式(16)求微分并作代换,得

利用初始条件:t=0时,有

对式(18)积分,得带电粒子的轨迹方程为:

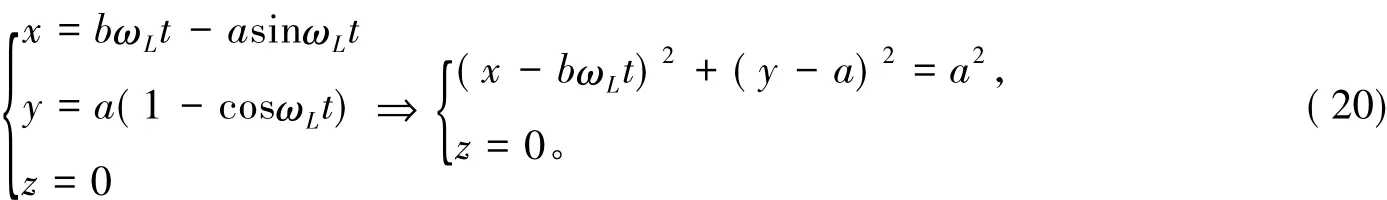
根据不同的初始速度与电磁场大小对式(20)进行数值模拟,模拟图如图5所示。
由图5可知,若v0<E/B时,带电粒子的轨迹是短幅摆线,如图5(a)所示;若v0>E/B时,带电粒子的轨迹是长幅摆线,如图5(b)所示;若v0=E/B时,带电粒子沿x轴作匀速直线运动,如图5(c)所示。
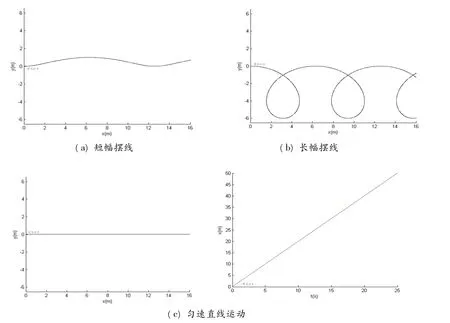
图5 带电粒子在均匀正交电磁场中的运动轨迹
2 带电粒子在电磁场中运动的普遍情况
2.1 带电粒子在均匀非正交电磁场中的运动
以上讨论了(1)只有电场而没有磁场;(2)只有磁场而电场为三者两两互相垂直的三种情况。现在讨论普遍情况下带电粒子在电磁场中的运动情况,即成任意夹角时,求解其运动规律。


图6 均匀非正交电磁场
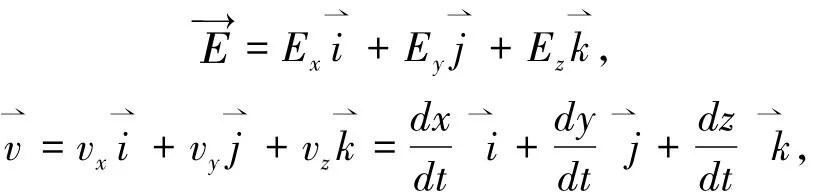
代入式(21),有
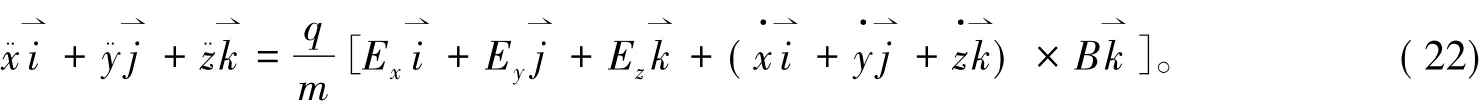
整理得一组微分方程:
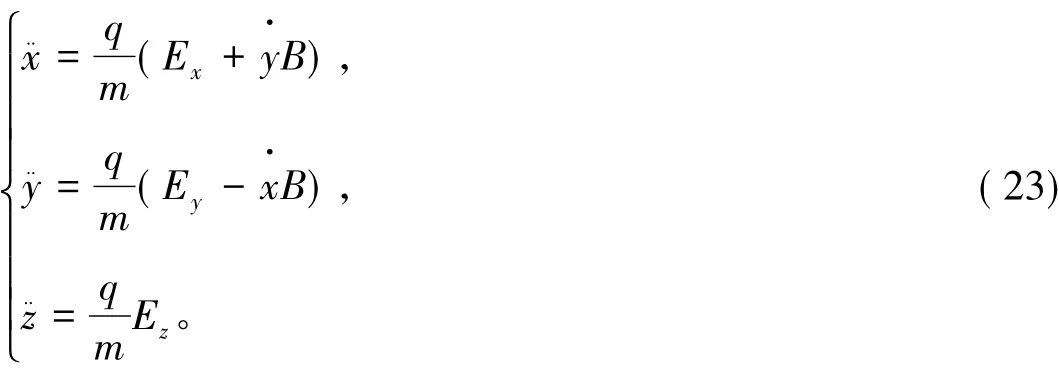
对式(23)微分并整理,得:

积分,得:

此为带电粒子在恒定电磁场中运动时其速度在x、y、z轴上的3个分量式。

图7 带粒子在匀强非正交电磁场中运动示意图

解式(26),得:
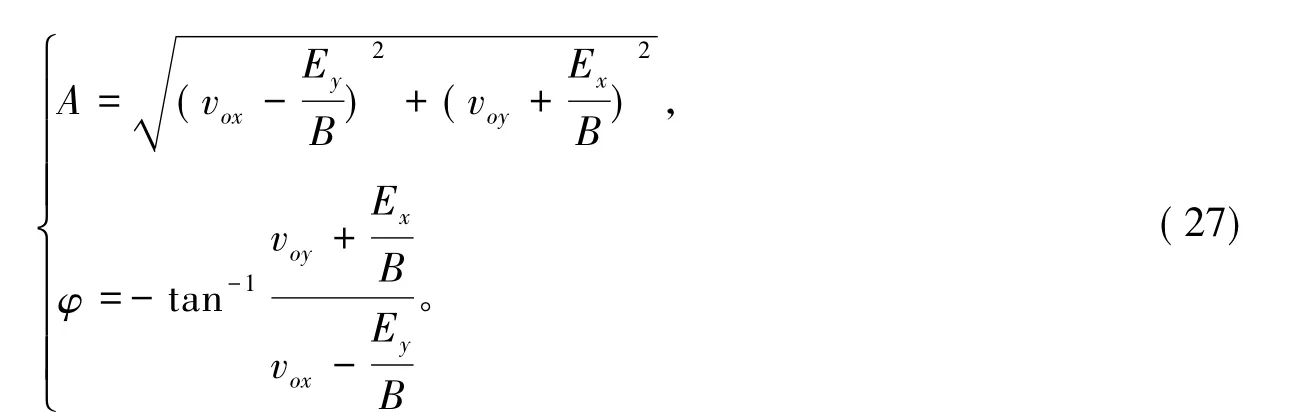
利用初始条件:在t=0时,带电粒子从原点开始运动,初速度为vo。即t=0时,有

并对式(28)积分得粒子的轨迹方程为:
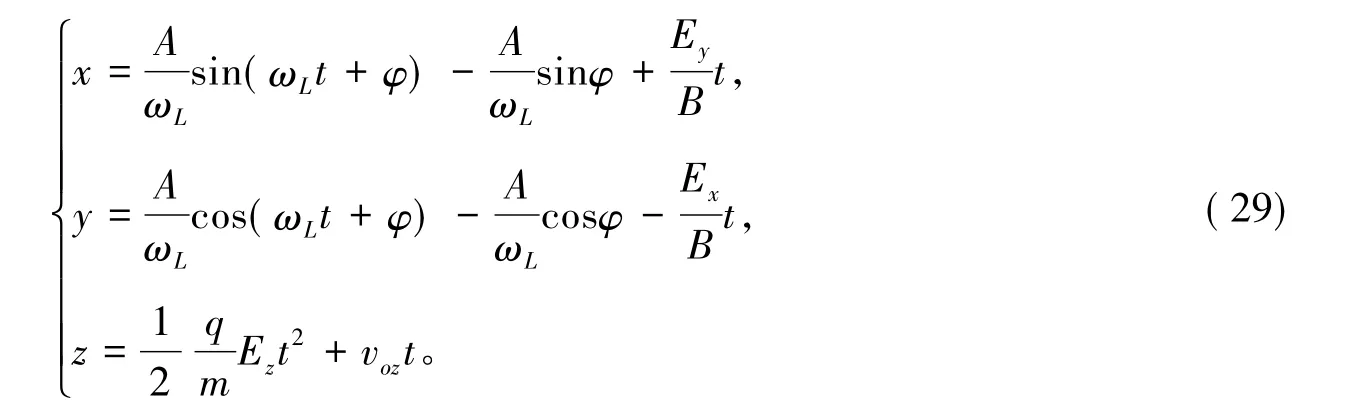
取Ex=1 N/C,Ey=Ez=2 N/C,vox=voy=2 m/s,voz=1 m/s进行模拟,轨迹曲线如图7所示。
由图7可知,在匀强非正交电磁场中运动的带电粒子,在xoy平面内作摆线运动,如图7(a)所示;在沿z轴方向作匀加速直线运动,如图7(b)所示;带电粒子在均匀非正交电磁场中的运动轨迹如图7(c)所示。

图8 非匀强磁场
2.2 带电粒子在非匀强磁场中的运动规律
带电粒子运动矢量微分方程为:

由于

粒子运动微分方程的分量形式为:

对式(32-3)积分,并利用初始条件可得

再积分,由于z(0)=0,可得

当θ=0时,vx=vy=0,因此粒子沿z轴作匀速直线运动。当θ=π/2时,vx=v0,vz=vy=0,在x=0的平面,B=0,粒子沿x轴作匀速直线运动。
再求解x方向和y方向的运动方程:由式(33-1)(33-2)得,

利用初始条件:vx=v0sinθ,vy=0得

设 vx=v0sinθcosφ,vy=v0sinθsinφ,φ 为角变量,代入式(32-1),则得

当t=0时,φ=0。对式(37)积分得
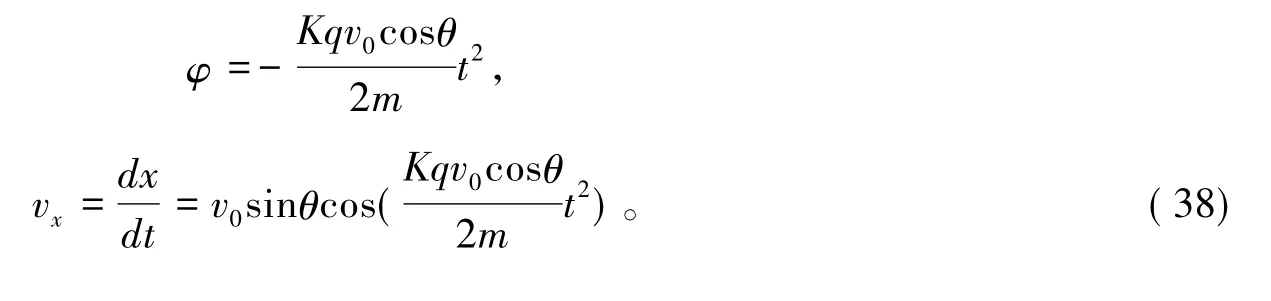
对式(38)积分得:

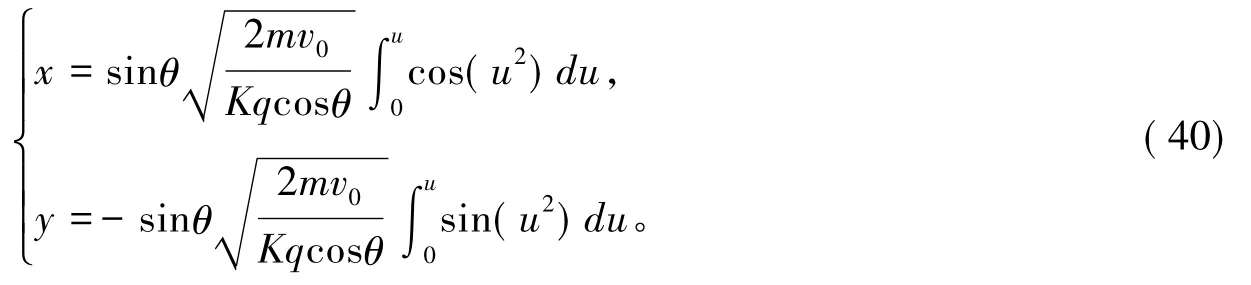
此积分称为菲涅尔余弦 /正弦积分,只有数值解。当积分上限趋于无穷大时,两个菲涅耳积分都趋于则粒子的极限坐标为:
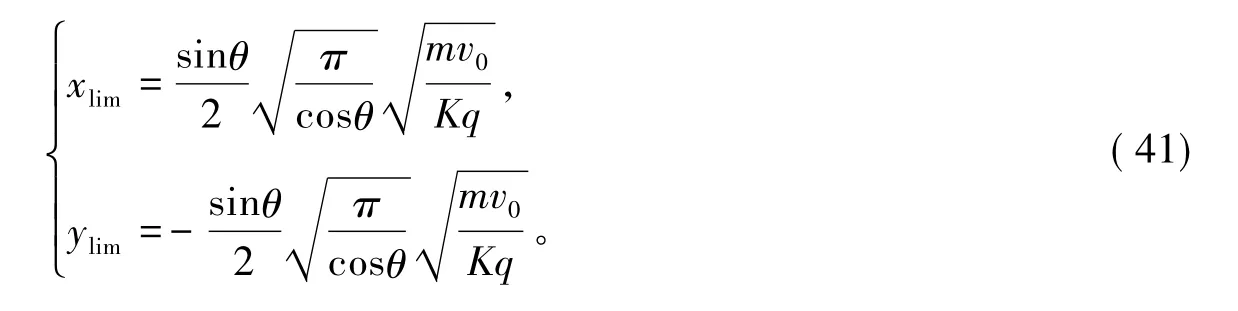

粒子的极限坐标为:

取θ=60°对式(42)进行模拟,得到带电粒子在非匀强磁场中的运动规律与轨迹,如图9(a)、图9(b)所示。
图9(a)之上图和中图表示,当带电粒子的入射角为60°时,其坐标x和y随时间均做周期性变化,时间越长,幅度越小。图9(a)之下图表示,带电粒子的z坐标随时间直线增加。图9(b)表示,带电粒子的运动轨迹是螺旋上升的,时间越长,粒子运动得越高,半径也越小。[6]由于磁场只有z分量,粒子在z方向作匀速直线运动,因此,粒子不会返回来。
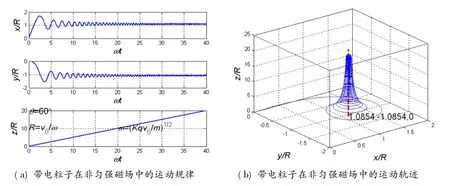
图9 带电粒子在非匀强磁场中运动的规律与轨迹
3 结语
借助MATLAB软件的作图动画功能,对带电粒子在电磁场中运动的5种情况进行模拟,将其运动规律形象而直观地描绘出来,加强了对带电粒子在电磁场中运动规律的理解和掌握,为进一步研究带电粒子在其他情况下的运动以及运动规律在科学技术中的应用提供科学参考。
[1]陈秉乾,舒幼生,胡望雨.电磁学专题研究[M].北京:高等教育出版社,2003.
[2]周博,谢东来,张宪海.MATLAB-科学计算[M].北京:机械工业出版社,2010.
[3]占亚波,于立志.计算机模拟带电粒子在电磁场中的运动[J].阜阳师范学院学报(自然科学版),2010,27(1):40-43.
[4]牛怀岗,朱志平.MATLAB 求解力学问题探析[J].渭南师范学院学报,2016,31(16):64-69.
[5]高永毅,张平柯.带电粒子在均匀电磁场中运动的普遍规律[J].湘潭师范学院学报,1996,17(3):84-87.
[6]欧阳钤,史兆宪.带电粒子在电磁场中运动的普遍情况[J].零陵师专学报,1981,2(1):47-59.
