一种高压直流断路器的混合式电弧模型

， ，

(河北工业大学 电气工程学院， 天津 300130)

断路器是电路中不可或缺的电器装置，起到接通或断开正常回路下电流以及迅速断开故障回路下电流的作用[1]。电弧总是出现在断路器开、断的时刻，因此断路器研究的关键是对断路器电弧的研究。电弧是非常复杂的物理过程，考虑到实验的局限性以及数值仿真技术的进步，电弧模型的建立成为研究电弧的首要任务，同时对于电弧相关特性的研究也有助于断路器技术，尤其是断路器灭弧技术的发展[2-3]。

当前，电弧模型分为微观模型和宏观模型2类[4]。其中微观模型是对电弧等离子体中发生的物理变化进行研究，初步的研究成果主要包括Eindhoven模型和Potapov模型[5]。应用最广的磁流体动力学模型在流体力学的基础上又考虑了热动力学以及麦克斯韦方程组[6]。在早期和目前微观模型的过渡时期，有关学者提出了流体力学、 粒子模拟、动力学方法[7-8]。宏观模型不考虑电弧内部的物理化学变化，对电弧宏观描述使用最多的是Cassie模型和Mayr模型[9-11]。两者的优点是原理和计算相对简单，但仅仅考虑了热力学和统计物理在电弧发生过程中的影响。流体模型计算速度相对较快，能体现粒子化学反应过程，但该模型是在一定的假设条件下建立的。粒子模拟方法比较真实地体现电弧物理过程，没有条件假设，缺点是计算量大。动力学模型相比流体模型和粒子模拟方法有了一定进步，但是适用范围有限。磁流体动力学模型考虑了各个因素对电弧的影响，深入研究了电弧发生过程中产生的一系列物理和化学上的变化，对电弧的研究有了更深的理解，但电弧是多个物理场耦合，耦合过程比较复杂。

Mayr模型和Cassie模型将电弧发生的物理变化与电路相关的特性有效地结合起来，形成了电弧的电学模型，对后来电弧的研究起到不可忽视的作用[12-14]，但是这2个模型都只是考虑了能量平衡理论。文献[15]中通过对现有模型的改进，增加并确定模型参数，将该电弧模型成功地应用在对高压断路器电弧特性的描述上。

本文中提出的混合式电弧模型结合了Mayr模型和Cassie模型各自的优点，通过连接函数调节2种模型在混合式电弧模型中所占的比例对电弧进行准确的数学建模。与以往电弧的应用环境不同，本研究是在直流条件下进行的。为了使电弧模型能更好地适用于直流系统，建立2种模型之间的连接函数，使其能在电弧电流较大或较小时调整Mayr模型和Cassie模型在混合式电弧模型中所占的比例，从而实现对电弧发生过程的准确建模，通过仿真实验来验证本文中提出的混合式电弧模型的准确性。

1 电弧模型的建立

1.1 Cassie模型和Mayr模型

通常，Cassie模型和Mayr模型都被认为是黑盒模型。黑盒模型的特点是对电弧宏观描述，用来表现电弧外特性，在建立电弧动态模型的基础上又便于仿真和建模。黑盒模型对断路器开、断能力研究具有一定意义[10]。

Cassie模型假设：气体通道是圆柱形；电弧气体通道有严格的边界，边界以外电导非常小；温度在截面上的分布是均匀的，并且不随电弧电流变化；随着电弧电流变化，电弧气体通道的直径也随着发生变化；忽略从电极散出的能量，认为能量散出是由电弧气体通道变化引起，且与气体通道横截面变化成正比[16]。Cassie模型在描述处于大电流(电弧电阻较小)区域的电弧时比较准确，根据假设条件，Cassie模型的具体表达式为

(1)

式中：u为电弧电压；gC为Cassie模型的电弧电导；E0为电弧电压常数；τ为电弧时间常数；g为电导；t为时间。

Mayr模型假设：体通道也认为是圆柱形，且轴向直径大小假设不变；忽略从电极散发的热量，且电弧散发的能量始终保持不变[16]。Mayr模型用于表示小电流大电阻的电弧，根据假设条件，Mayr模型的表达式为

(2)

式中：gM为Mayr模型的电弧电导；i为电弧电流；P0为电弧散热功率。

综上，Cassie模型和Mayr模型都是以电弧气体通道能量守恒为基础建立的，且假设的电弧气体通道方向都是不变的。这2种模型的区别主要在于电弧能量散失的方式不同，这决定了它们应用场所的不同。

1.2 混合模型的建立

Mayr模型和Cassie模型分别应用在电弧的小电流区域和电弧的大电流区域准确性较高，但根据电弧特性可知，电弧的小电流区域和大电流区域同时存在；因此不可能用黑盒模型中任何一种单一的电弧模型对电弧进行较准确描述，需要将2个模型结合起来进行描述。2个模型的结合能更好地展现不同电流区间的电弧特性，但两者的结合需要一个连接函数。连接后的模型表达式为

(3)

式中：garc为连接函数电导值；imax、imin分别为电弧电流的上、下限值。

设计此连接函数的主要目的是通过在电流大小不同时切换Mayr模型和Cassie模型来达到利用组合式电弧模型对电弧发生到熄灭整个过程进行完整描述的目的。从式(3)中可以看出，当电弧处于小电流区域时，gM在garc中所占的比例较大，Mayr模型在电弧的描述中起主要作用；当电弧处于大电流区域时，gC在garc中所占的比例逐渐增大，电弧的描述开始以Cassie模型为主。这样，通过此连接函数的设计，建立了由2种模型结合形成的混合式电弧模型，提高了电弧特性数学模型的准确性，相比于任何一种单一模型都更符合电弧的实际情况。

2 仿真实验及结果分析

2.1 仿真参数选取及模型建立

由混合式电弧模型式(3)可以看出，在仿真过程中，需要设置的参数有电弧电压常数E0、电弧时间常数τ和电弧散热功率P0。本文中首先对这3个参数取不同值时的情况进行仿真实验，结果如图1—3所示。

从图1中可以看出，电弧电压随着时间的变化有逐步增大的趋势，当增大到一定程度时，会经过短时的振荡过程而保持稳定。电弧电压常数E0决定着电弧电压处于稳态时的大小，E0越大，电弧电压最终的稳态值也就越大。

从图2中可以看出，电弧时间常数τ和电弧电压的主要影响表现在电弧电压开始振荡的时间和振荡的幅度上。电弧时间常数τ越大，电弧电压出现振荡的时间越晚，但振荡的时间越长，振荡的幅度也就会越大。

图1 电弧电压常数E0不同时的电弧电压波形图

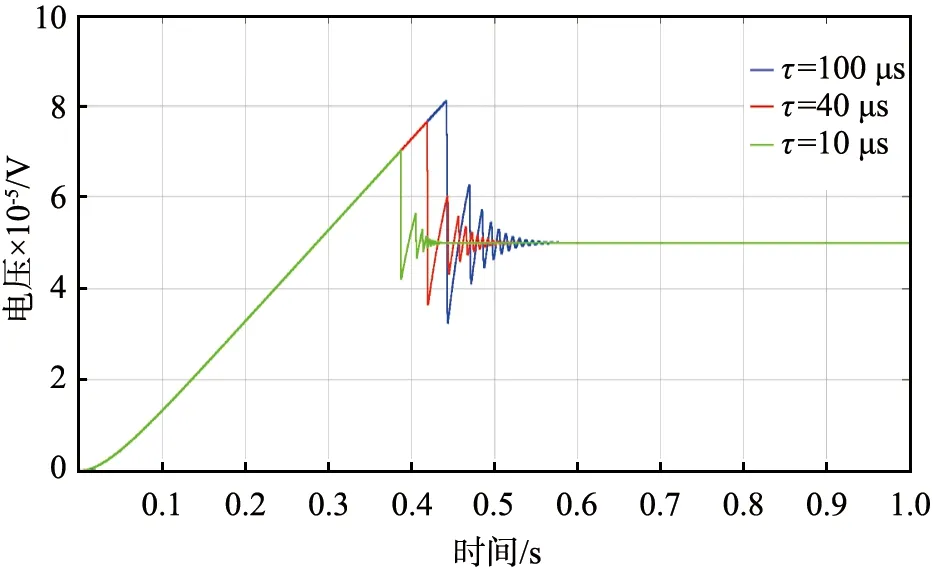
图2 电弧时间常数τ不同时的电弧电压波形图

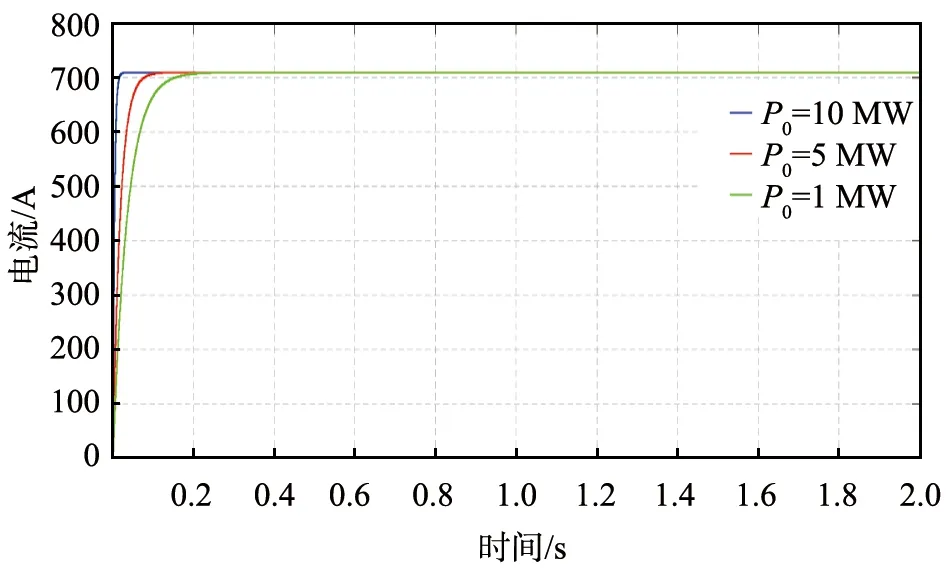
图3 电弧散热功率P0不同时的电弧电流波形图

从图3中可以看出，电弧散热功率P0主要对电弧电流的变化趋势产生影响， 影响的是电弧电流处于暂态过程的时间。电弧散热功率P0越大，电弧电流处于暂态过程的时间就会越短，电流保持稳定的时间越长。

基于上述对电弧时间参数的分析，并经过多次的仿真实验对比，本文中最终选择的混合式电弧模型仿真参数如表1所示。

表1 混合式电弧模型仿真参数

根据表1中对高压直流真空电弧所设置的仿真参数，在MATLAB/Simulink软件中建立如图4所示的仿真结构，对混合式电弧模型的准确性进行仿真实验验证。

2.2 电弧时间特性仿真结果及分析

首先对现有的Mayr模型和Cassie模型进行直流电弧时间特性的仿真实验，结果如图5所示。

从图中可以看出，在0.2 s电弧出现后，Cassie模型的电弧电压迅速跃升至开路电压值，曲线较为平滑，所以Cassie电弧模型只适于描述电弧电流较大时的情景。Mayr模型的电弧电压在最初的一段时间中没有发生变化，之后发生了较为剧烈的振荡，虽然幅值较小，但振荡的时间很长；所以Mayr电弧模型只适于描述电弧电流较小时的情景。

对提出的混合式电弧模型进行直流电弧时间特性的仿真实验，仿真实验结果及相关区域的放大图如图6—9所示。

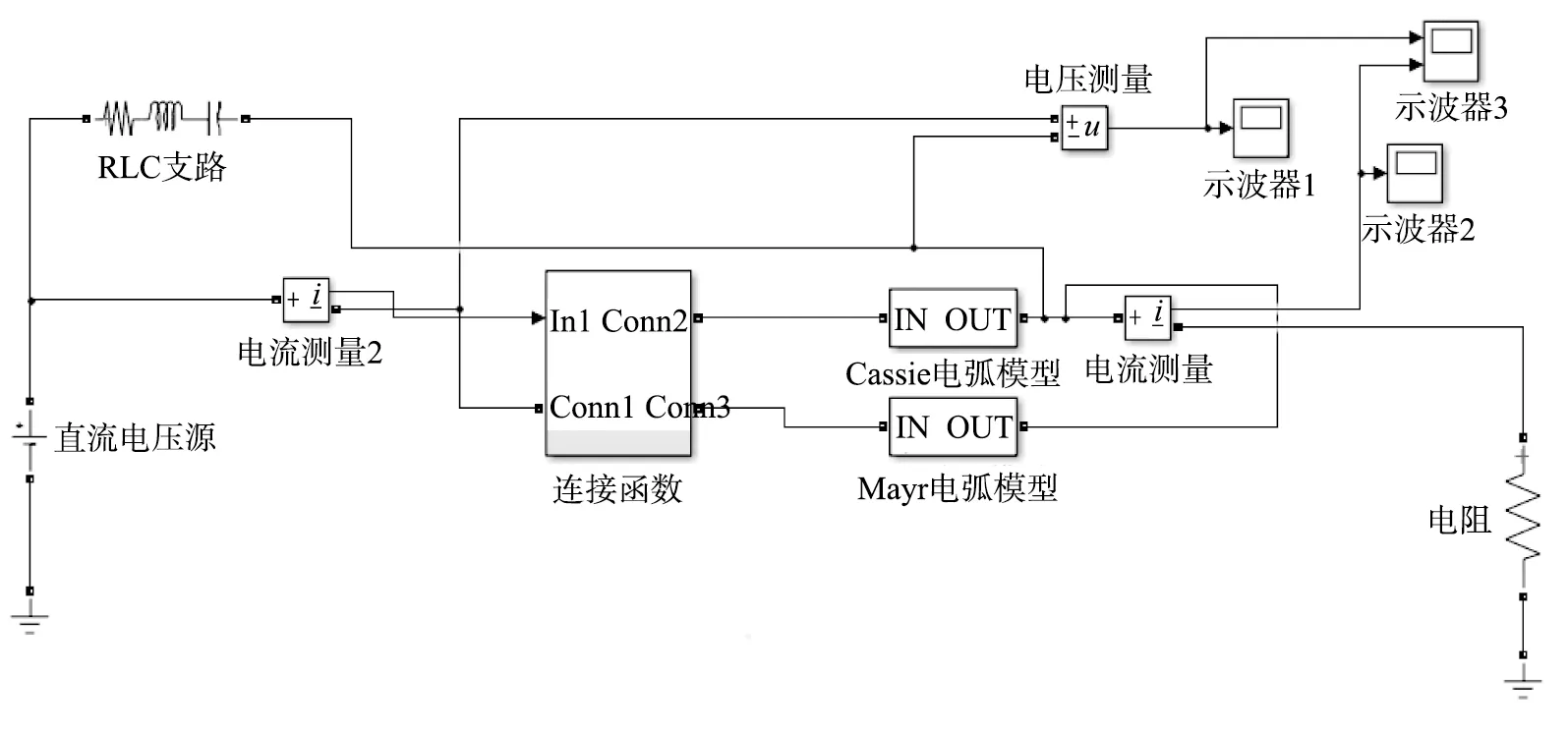
图4 仿真模型结构图

图5 Cassie模型及Mayr模型电弧电压波形图

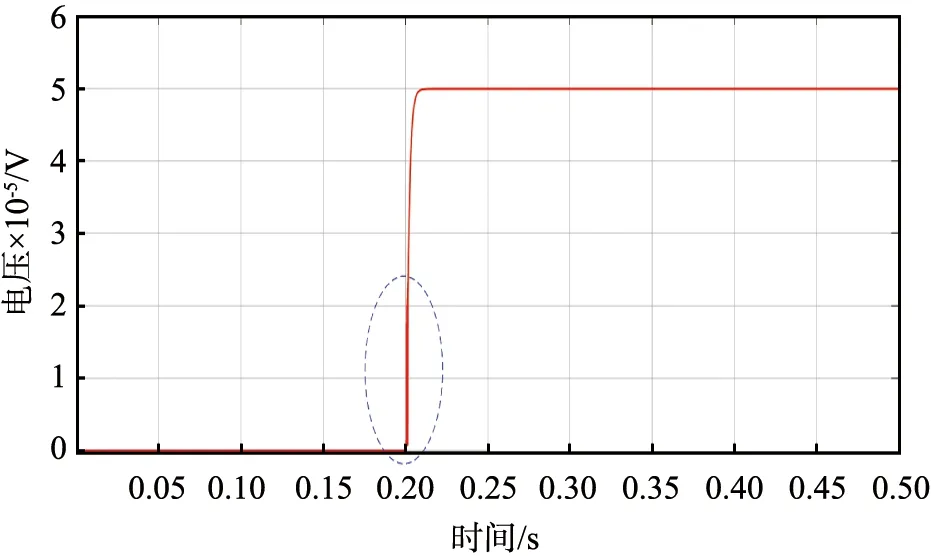
图6 混合模型电弧电压波形图

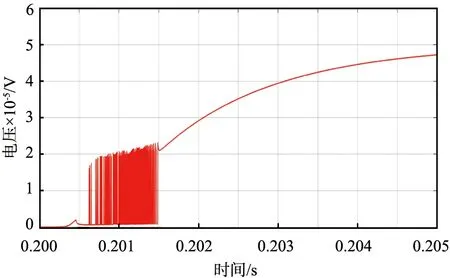
图7 混合模型电弧电压细节放大图

图8 混合模型电弧电流波形图

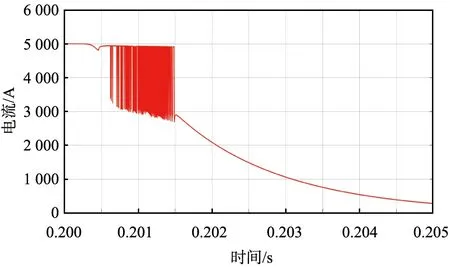
图9 混合模型电弧电流细节放大图

从图6—9中可以看出，在0.2 s电弧产生后，混合电弧模型的电弧电压及电弧电流的时间特性曲线的整体走势与Cassie模型基本相同，但在电弧刚刚发生的时间段内，电弧电压及电弧电流均出现了振荡的情况，这符合Mayr模型的情况，此现象存在约0.01 s后消失。由以上分析可以得出结论，本文中提出的混合模型有效地结合了Cassie模型和Mayr模型的电弧时间特性，对直流电弧时间特性的不同阶段准确地进行了数学描述，实现了对电弧发生全过程的准确建模。

3 结论

本文中建立了一个关于电弧电导的连接函数，即将Mayr模型和Cassie模型有机结合起来，进而提出一种高压直流断路器的混合式电弧模型，并对该混合式电弧模型的电压常数、时间常数等参数的选择进行了讨论和分析。根据选定的合理的混合电弧模型的参数，通过在MATLAB/Simulink软件中建立仿真实验模型的方式对所提出的混合式电弧模型进行了电弧的时间特性仿真实验分析。仿真实验结果表明，本文中所提出的混合式电弧模型对电弧的时间特性的描述精度均高于单一的Mayr电弧模型或Cassie电弧模型，实现了对于高压直流断路器中电弧发生全过程的准确建模，对高压直流断路器的灭弧技术研究有一定的指导意义。

[1] 刘晓明. 高压直流断路器电弧特性仿真研究[C]//中共沈阳市委员会，沈阳市人民政府，中国科学院沈阳分院.第十届沈阳科学学术年会论文集(信息科学与工程技术分册)，沈阳，2013:138-144.

[2] 舒胜文, 黄道春, 阮江军. 真空开关电弧开断过程的数值仿真方法研究进展[J]. 高压电器, 2014， 50(2):131-138.

[3] YUAN T, WANG Y. Research on high voltage switching Arc model based on MATLAB[C]//nternational Conference on Consumer Electronics, Communications and Networks. New York: IEEE, 2011:2508-2511.

[4] 黄绍平，杨青，李靖. 基于MATLAB的电弧模型仿真[J].电力系统及其自动化学报, 2005,17(5)：64-66，70.

[5] 刘春园. 磁场对真空电弧等离子体特性的影响研究[D]. 沈阳：沈阳工业大学, 2015.

[6] 李争博. 开关电弧等离子体输运特性的计算[D]. 沈阳：沈阳工业大学, 2012.

[7] 王毅, 王季梅. 真空电弧等离子体弧柱现象模型分析[J]. 中国电机工程学报, 1992(5):53-57.

[8] 李静, 曹云东, 邹积岩, 等. 直流气体放电过程中的离子分子碰撞模型[J]. 高电压技术, 2009, 35(7):1677-1682.

[9] 李静, 曹云东, 王尔智, 等. 断路器短间隙气体击穿过程的粒子模拟[J]. 中国电机工程学报, 2010, 30(16):125-130.

[10] 薄凯. 真空动态电弧微观机理研究[D]. 沈阳：沈阳工业大学, 2014.

[11] THOMAS D W P, PEREIRA E T, CHRISTOPOULOS C, et al. The simulation of circuit breaker switching using a composite Cassie-modified Mayr model[J]. IEEE Transactions on Power Delivery, 1995, 10(4):1829-1835.

[12] GUARDADO J L, MAXIMOV S G, MELGOZA E, et al. An improved arc model before current zero based on the combined Mayr and Cassie arc models[J]. IEEE Transactions on Power Delivery, 2005, 20(1):138-142.

[13] BIZJAK G, ŽUNKO P, POVH D. Circuit breaker model for digital simulation based on Mayr’s and Cassie’s differential arc equations[J]. IEEE Transactions on Power Delivery, 1995, 10(3):1310-1315.

[14] 戴隽文, 郝瑞祥, 游小杰. 一种用于大功率电弧加热器的等离子电弧模型[J]. 电工技术学报, 2011, 26(1):129-134.

[15] 贾恒, 罗隆福, 许加柱. 高压断路器KEMA电弧模型改进研究[J]. 电力自动化设备, 2012, 32(9):134-137.

[16] 孙袆. 低压交流接触器电弧动态数学模型和温度场仿真研究[D]. 北京:华北电力大学, 2010.