集值向量优化问题的Henig有效解的最优条件
2018-03-10,
,
(1. 华东交通大学 理工学院, 江西 南昌 330100; 2. 南昌大学 数学系, 江西 南昌 330031)
集值优化理论在不动点、变分学、微分包含、最优控制、工程技术、交通平衡等领域具有广泛的应用,学者们从不同的角度进行深入研究,取得了一系列丰硕的成果。在最优性条件中,凸性具有十分重要的作用,凸性概念在不断被推广。Yang等[1-2]分别引进广义锥-次类凸和近似锥-次类凸集值映射,并研究其关系。Sach[3]引进一种新的凸性——内部锥-类凸性,并建立了新的择一性定理,得到有效解、弱有效解和Benson真有效解意义下的 Kuhn-Tucker型和Lagrange型最优性条件。在近似锥-次类凸假设下,文献[4-6]中给出了超有效解Lagrange型最优性条件及强有效解的Kuhn-Tucker型最优性条件。文献[7-9]中提出了严有效点的概念,它有非常好的性质,即每个严有效点都能用严格正泛函来标量化,同时保持了超有效点的主要特征,而且存在条件比超有效点弱得多。Cheng等[10]在局部凸拓扑线性空间中,引入强有效解的概念,推广了超有效性和严有效性,并且具有良好的性质,即强有效解能用基泛函来标量化。Zheng[11-12]将Henig有效点和全局有效点的概念由赋范空间推广到局部凸空间。超有效性、 严有效性和强有效解的存在条件是很强的, 在很多情况下很难实现。 Henig有效性保持了超有效性、 严有效性和强有效解的主要特征, 而存在条件弱很多, 仅要求序锥具有基底,目前研究较少, 因此, 对集值优化问题Henig有效性的研究具有重要的理论价值。 Jahn等[13]在拓扑向量空间中提出相依上图导数的概念, 研究了集值优化问题相依上图导数的性质。Qiu[14]在相依上图导数的基础上给出广义锥-凸集值映射,讨论了有效解的最优性条件。本文中借助相依上图导数和广义锥-凸集值映射的概念,在实拓扑向量空间中研究集值向量优化问题Henig有效解和向量变分不等式Henig有效解之间的关系。
1 预备知识
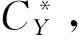
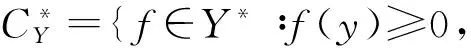
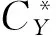
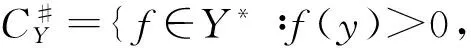
设D是Y的非空子集,D的闭包记为cl(D),且D的锥包定义为
cone(D)={ty∶t≥0,y∈D}。

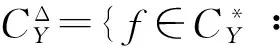
r=inf{f(b)∶b∈BY}>f(0Y)=0。
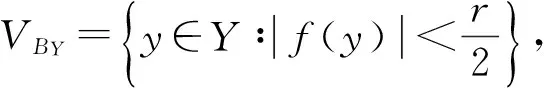
对每个零元凸邻域U⊂VBY,均有BY+U为凸集且0Y∉cl(BY+U),因此,CU(BY)∶=cone(BY+U)为点凸锥,且CY{0Y}⊂intCU(BY)。记
∑={CU(BY)⊂Y∶CU(BY)为点凸锥且
CY{0Y}⊂intCU(BY)}。
定义1[15]设D⊂Y为非空子集,称点y0∈D为集合D的Henig有效点,如果存在点凸锥CU(BY)∈∑,使得
cone(D-y0)∩[-intCU(BY)]=/○。
注1 由文献[16]可知,设D⊂Y为非空子集,点y0∈D为集合D的Henig有效点当且仅当存在点凸锥CU(BY)∈∑,使得
(D-y0)∩[-intCU(BY)]=/○。
设A⊂X为非空子集,G∶X→2Y为给定集值映射,即对每个x∈X,有G(x)⊂Y。
集合graph(G)={(x,y)∈A×Y∶y∈G(x)}称为映射G的图。
集合epi(G)={(x,y)∈A×Y∶y∈G(x)+CY}称为映射G的上图。
设(x0,y0)∈graph(G),由文献[17]可知,上图epi(G)在(x0,y0)处的相依锥记为T[epi(G),(x0,y0)],包含了在该点的所有切线向量。
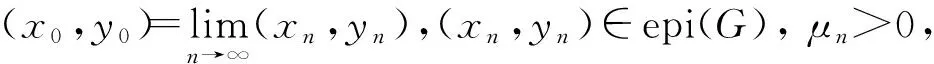
定义2[13]设(x0,y0)∈graph(G)给定,向量值映射DG(x0,y0)∶X→Y的上图等于集值映射G的上图在(x0,y0)处的切锥,即
epi[DG(x0,y0)]=T[epi(G),(x0,y0)],
称DG(x0,y0)为G在(x0,y0)处的相依上图导数。
注2[13]设(x0,y0)∈graph(G)给定,且相依上图导数DG(x0,y0)存在,则DG(x0,y0)为正齐次的。
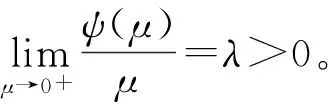
μG(x)+(1-μ)G(y)⊂G[x0+ψ(μ)ζ(x,y)]+CY。
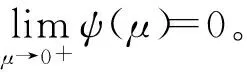
现在考虑集值向量优化问题(SVOP):
其中A⊂X为非空子集,G∶X→2Y为给定集值映射。
定义4 1)称(x0,y0)∈graph(G)为SVOP的Henig有效解,如果存在点凸锥CU(BY)∈∑,使得
[G(A)-y0]∩[-intCU(BY)]=/○。
2)称(x0,y0)∈graph(G)为SVOP的局部Henig有效解, 如果存在点x0的邻域V(x0)以及点凸锥CU(BY)∈∑, 使得
{G[A∩V(x0)]-y0}∩[-intCU(BY)]=/○。
下面给出一类向量变分不等式的Henig有效解的概念。
设x0∈A,y0∈G(x0),ζ(A,x0)={ζ(x,x0)∶x∈A}包含于相依上图导数DG(x0,y0)的定义域。
考虑向量变分不等式问题(VVIP),即寻找x0∈A,y0∈G(x0),使得
DG(x0,y0)[ζ(x,x0)]∉-intCU(BY),∀x∈A,
其中K∪{0Y}为Y中的点凸锥。
定义5 称(x0,y0)∈graph(G)为VVIP的Henig有效解,如果存在点凸锥CU(BY)∈∑,使得
DG(x0,y0)(ζ(x,x0))∉-intCU(BY),∀x∈A。
2 最优性条件
为了研究集值向量优化问题的Henig有效性,由文献[18]可知,相依上图导数具有如下性质。
引理1[18]设A⊂X关于ζ和ψ为广义凸子集,G∶A→2Y在A上关于ζ和ψ为广义CY-凸集值映射。 假定x0∈A,y0∈G(x0), 且相依上图导数DG(x0,y0)存在,则
G(x)-{y0}⊂{λDG(x0,y0)[ζ(x,x0)]}+CY,∀x∈A,
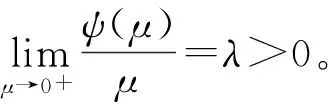
设G为SVOP中的广义CY-凸集值映射,则SVOP的局部Henig有效解即为SVOP的Henig有效解。
引理2 设A⊂X关于ζ和ψ为广义凸子集,G∶A→2Y在上关于ζ和ψ为广义CY-凸集值映射。如果(x0,y0)∈graph(G)为SVOP的局部Henig有效解,则(x0,y0)∈graph(G)为SVOP的Henig有效解。
证明: 设(x0,y0)∈graph(G)为SVOP的局部Henig有效解,由定义4的2)可知,存在点x0的邻域V(x0)及点凸锥CU(BY)∈∑,使得
{G[A∩V(x0)]-y0}∩[-intCU(BY)]=/○。
(1)
反证法。假设(x0,y0)不是SVOP的Henig有效解,则存在x*∈A,y*∈G(x*)使得
y*-y0∈-intCU(BY)。
(2)
由A关于ζ和ψ为广义凸集,根据定义3可知,
x0+ψ(μ)ζ(x*,x0)∈A,∀μ∈(0,1)。
由此,存在μ0∈(0,1),使得
x0+ψ(μ)ζ(x*,x0)∈V(x0),∀μ∈(0,μ0),
于是
x0+ψ(μ)ζ(x*,x0)∈V(x0)∩A,∀μ∈(0,μ0)。
(3)
另一方面,由G在A上关于ζ和ψ为广义CY-凸集值映射,由定义3可知,对任何μ∈(0,μ0),有
y0+μ(y*-y0)=μy*+(1-μ)y0∈
μG(x*)+(1-μ)G(x0)⊂
G(x0+ψ(μ)ζ(x*,x0))+CY。
结合式(2)可知,
μ(y*-y0)∈-intCU(BY)。
于是
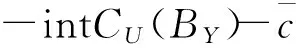
-intCU(BY)-CY⊂-intCU(BY)。
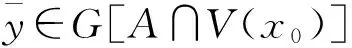
这与式(1)矛盾。引理1得证。
借助集值映射的相依上图导数与广义凸集值映射的性质,分析SVOP的Henig有效解和VVIP的Henig有效解之间的紧密关系。
设x0∈A,y0∈G(x0),相依上图导数DG(x0,y0)存在,且ζ(A,x0)={ζ(x,x0) ∶x∈A}包含于DG(x0,y0)的定义域。
定理1 设(x0,y0)为SVOP的Henig有效解,则(x0,y0)为VVIP的Henig有效解。
证明: 设(x0,y0)∈graph(G)为SVOP的Henig有效解, 则根据注1可知, 存在点凸锥CU(BY)∈∑,使得
[G(A)-{y0}]∩[-intCU(BY)]=/○。
(4)
反证法。假设存在x*∈A满足
y*=DG(x0,y0)[ζ(x*,x0)]∈-intCU(BY)。
(5)
由相依上图导数的定义可知,
(ζ(x*,x0),y*)∈epi[DG(x0,y0)]=T[epi(G),(x0,y0)],
因此存在(xn,yn)∈epi(G)及正实数序列{μn},满足
且
于是
(6)
由式(5)、(6)知,存在N0∈,有
μn(yn-y0)∈-intCU(BY),∀n≥N0。
从而
yn∈{y0}-intCU(BY),∀n≥N0。
(7)
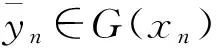
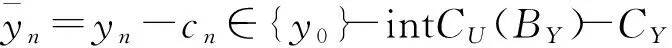
{y0}-intCU(BY)-CU(BY)⊂
{y0}-intCU(BY),∀n≥N0。
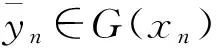
这与式(4)矛盾。定理1得证。
定理2 设A⊂X关于ζ和ψ为广义凸子集,G∶A→2Y在A上关于ζ和ψ为广义CY-凸集值映射。设(x0,y0)为VVIP的Henig有效解,则(x0,y0)为SVOP的Henig有效解。
证明: 由假设知,存在点凸锥CU(BY)∈∑,使得
DG(x0,y0)[ζ(x,x0)]∉-intCU(BY),∀x∈A。
(8)
由CU(BY)为点凸锥且λ>0可知,
λDG(x0,y0)[ζ(x,x0]∉-intCU(BY),∀x∈A。
反证法。假设(x0,y0)不是SVOP的Henig有效解,则存在x*∈A,y*∈G(x*),满足
y*-y0∈-intCU(BY)。
由引理1可知,存在c*∈CY,使得
y*-y0=λDG(x0,y0)[ζ(x*,x0)]+c*,
因此,
λDG(x0,y0)[ζ(x*,x0)]=
y*-y0-c*∈-intCU(BY)-CY⊂-intCU(BY)。
这与式(8)矛盾。定理2得证。
3 结论
1)在实拓扑向量空间中,引进一类SVOP和VVIP,给出SVOP的Henig有效解、局部Henig有效解与VVIP的Henig有效解的概念。
2)借助于相依上图导数的概念,在广义锥-凸集值映射下,得到SVOP的Henig有效解与VVIP的Henig有效解是一致的结论。
3)运用研究集值向量优化问题Henig有效性的基本思想,研究含参集值向量优化问题Henig有效性、全局有效性和超有效性是有意义的课题。
[1] YANG X M, YANG X Q, CHEN G Y. Theorems of the alternative and optimization with set-valued maps[J]. J Optim Theory Appl, 2000, 107(3): 627-640.
[2] YANG X M, LI D, WANG S Y. Nearly-subconvexlikeness in vector optimization with set-valued functions[J]. J Optim Theory Appl, 2001, 110(2): 413-427.
[3] SACH P H. New generalized convexity notion for set-valued maps and application to vector optimization[J]. J Optim Theory Appl, 2005, 125(1): 157-179.
[4] XU Y H, ZHU C X. On super efficiency in set-valued optimization in locally convex spaces[J]. Bull Austral Math Soc, 2005, 71(2): 183-192.
[5] XU Y H, LIU S Y. Super efficiency in the nearly cone-subconvexlike vector optimization with set-valued functions[J]. Acta Math Scientia, 2003, 25(1): 95-102.
[6] 徐义红. 集值优化问题强有效解的Kuhn Tucker最优性条件[J]. 数学研究与评论, 2006, 26(2): 354-360.
[7] 傅万涛. 赋范线性空间集合的严有效点[J]. 系统科学与数学, 1997, 17(4): 324-329.
[8] FU W, CHENG Y. On the strict efficiency in a locally convex space[J]. Sys Math Scis, 1999, 12(1): 40-44.
[9] 傅万涛, 陈晓清. 逼近锥族和严有效点[J]. 数学学报, 1997, 40(6): 933-938.
[10] CHENG Y H, FU W T. Strong efficiency in a locally convex space[J]. Mathematical Methods of Operations Research,1999, 50(3): 373-384.
[11] ZHENG X Y. Proper efficiency in locally convex topological vector spaces[J]. J Optim Theory Appl, 1997, 94(2): 469-486.
[12] ZHENG X Y. The domination property for efficiency in locally convex spaces[J]. J Math Anal Appl, 1997, 213(213): 455-467.
[13] JAHN J, RAUH R. Contingent epiderivatives and set-valued optimzation[J]. Mathematics Methods of Operation Research,1997,46(2): 193-211.
[14] QIU J H. Cone-directed contingent deriatives and generalized preinvex set-valued optimization[J]. Acta Mathematica Scientia, 2007, 27(1): 211-218.
[15] HENIG M I. Proper efficiency with respect to cones[J]. J of Optim Theory Appl, 1982, 36(3): 387-407.
[16] GONG X H. Optimality conditions for Henig and globally proper efficient solutions with ordering cone has empty interior[J]. J Math Anal Appl, 2005, 307(1): 12-31.
[17] JAHN J, RAUH R. The existence of contingent epiderivatives for set-valued maps[J]. Applied Mathematics Letters, 2003, 16(8): 1179-1185.
[18] YU G L. Henig globally efficiency for set-valued optimization and vector variational inequality[J]. J Syst Sci Complex, 2014, 27(2): 338-349.
