3类图像稀疏表示的去噪性能研究

，

(海南大学 机电工程学院， 海南 海口 570228)

图像去噪是图像的前期处理中一种重要的预处理方式，可以有效增强画面质量，提高信噪比。其最终目标是尽可能地将原始图像信息与噪声信号分离，消除噪声信号，还原图像的真实信号。 噪声对图像的影响类型分为加性噪声与乘性噪声， 前者指的是噪声信息与图像信号的线性叠加， 后者是指图像的噪声项是非线性的[1-3]。本文中主要研究常见的加性噪声，因为其与图像信号呈非线性相关，并不是原始图像的组成成分，所以可利用稀疏变换将其进行分离，实现噪声的去除或减弱。

稀疏变换有3类正交基函数，分别为二维离散余弦变换(DCT)、离散小波变换(DWT)、奇异值分解(SVD)。目前，这3种稀疏变换在图像领域中的应用是图像压缩、图像主成分分析等，尚未在图像去噪方面分析各自降噪的性能优劣[4]。本文中就此着手，对含高斯噪声污染的图像进行稀疏变换，提取出图像的稀疏结构，重构主成分，获得降噪后的图像，比较其性能，得出这3类稀疏矩阵的综合评价。

1 3类含高斯噪声图像的稀疏变换与重构

实际生活中的图像往往会受到加性的类高斯噪声的污染，来源一般是由拍摄设备的电子线路、低照明度等带来的[4]，因此，可在原始图像上叠加高斯噪声近似模拟实际受污染的图像。二维图像中的任意点M(i,j)的高斯噪声的分布模型为

(1)

式中：ζi, j表示M(i,j)的灰度值；μ为ζi, j的均值；σ为ζi, j的标准差；σ2为ζi, j的方差。

实际上，图像的噪声往往是均值μ为0的高斯白噪声。高斯噪声的ζi, j集中在μ附近，其密集程度取决于标准差σ，ζi, j值距离均值越远，噪声分布的范围越小[5]。设Y(i,j)为受高斯噪声影响的图像，而X(i,j)为原始图像，则噪声图像的理想退化式为

X(i,j)=Y(i,j)-Ni, jζi, j。

(2)

1.1 离散余弦变换与重构

DCT在JPEG图像压缩方面取得了良好的成效，其原理是将图像线性变换成一组系数，可以将带有图像大部分信息的多数系数量化和编码，实现以较小值的稀疏系数矩阵实现最大化的压缩[6]。图像的去噪可以借鉴这个原理，即在对噪声图像进行稀疏分解后，提取代表图像主要特征的近似系数，确定最佳去噪性能的系数个数，经由DCT反变换重构噪声退化后的图像。二维图像的DCT表示为

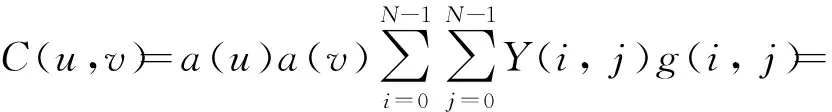
(3)

(4)

式中：u、v、i、j均表示图像点的坐标，取值范围为u、v、i、j=0, 1, 2, …,N-1，N为整数;a(u)为坐标u的幅值；a(v)为坐标v的幅值；g(i,j)表示余弦变换。其理想的图像去噪后的反变换重构式为

(5)

1.2 离散小波变换与重构

图像的离散小波分解中，每完整稀疏变换一次，经过不同低通滤波器h和高通滤波器g的分解后，获得4个分量，包括表示近似系数的低频分量和表示细节系数的3个高频分量dψ(n,m)。其中高频分量为图像矩阵的3个矢量方向上的小波系数，分别为水平、垂直和对角方向[7-9]。

(6)

(7)

(8)

(9)

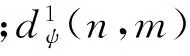
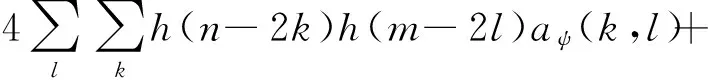
(10)

式中(k,l)为图像的分辨率索引。

由于高斯噪声信号混合在图像的高频分量dψ(n,m)中，因此可以考虑去掉高频分量，保留图像最主要的低频分量aψ(n,m)，利用其进行近似反变换重构，

(11)

1.3 奇异值分解与重构

图像像素可视为一个实矩阵， 对于任意的实数矩阵Xi×j， 可以通过奇异值分解来进行正交分解， 得到2个正交矩阵Ui×j、Vj×j和对角阵Di×j， 则SVD模型为

(12)

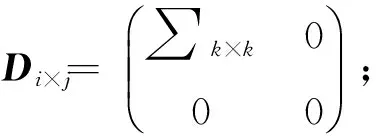
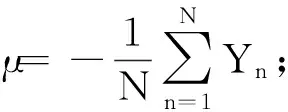
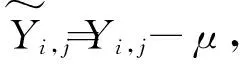
4)计算协方差矩阵的奇异值σi和特征向量ui；

5)选取前d个∑d×d=diag(σ1,σ2,…,σd)和Ud=(u1,u2,…,ud)；

2 仿真实验

灰度直方图描述了输入图像各个灰度级分布情况和发生概率。该图像直方图的横坐标与纵坐标分别对应灰度级g(0≤g≤l-1)和灰度级的频数Ng。利用MATLAB工具中的Cameraman.tif图像，并分别添加标准差为σ=10、 20、 30、 40、 50的高斯噪声，作为实验图像。根据原始图像和含高斯噪声图像绘制灰度直方图，如图1所示。

从图中可以看出，Cameraman的原始图像与含高斯噪声图像具有相同的双峰特性， 而原图受到高斯噪声污染后，灰度值较小的部分削弱，灰度值较大的部分得到补偿，并且有所增加，即高斯噪声的添加并不影响图像的主体结构，而是改变灰度分布情况。根据上述结论，可以通过对噪声图像的稀疏分解，得到图像的主要结构，再经过反变换重构图像，便可以实现噪声图像的去噪。

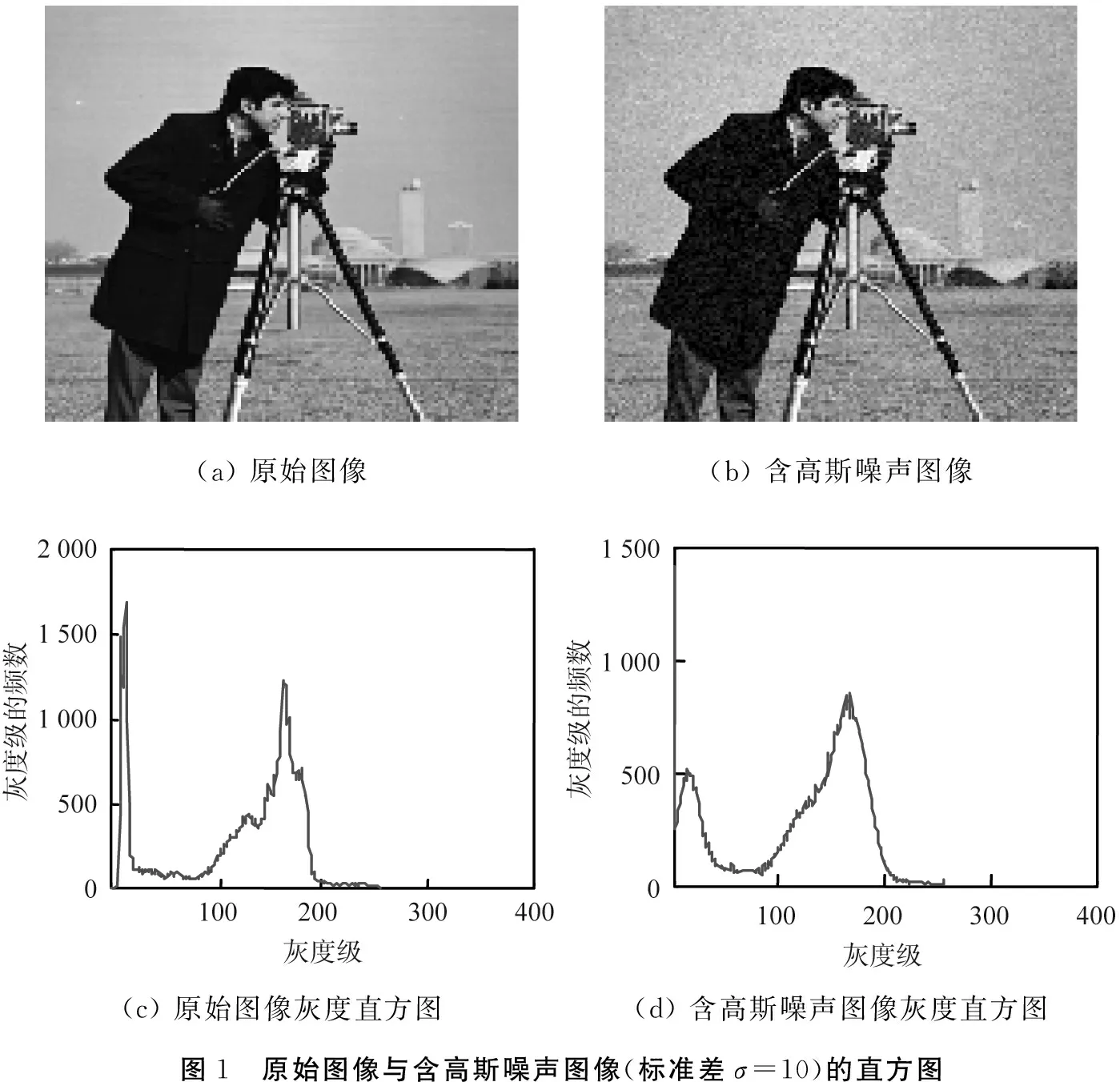
(a)原始图像(b)含高斯噪声图像(c)原始图像灰度直方图(d)含高斯噪声图像灰度直方图图1 原始图像与含高斯噪声图像(标准差σ=10)的直方图

在DCT稀疏变换与重构中，本文中采用DCT系数矩阵的8×8的窗口滑动方式逐一分解噪声图像，并取低频系数方阵中的左上角10个系数，此时重构的细节性较强[12]；对于DWT中的重构方式来说，则是根据DWT的近似反变换公式(式(10))来实现低频分量重构和高频分量去除，小波类型选择db4小波；而SVD算法只考虑使用60个特征值作为主成分，原因是在仿真过程中发现，低频系数的取值越小时，去噪图像清晰度下降越大，取60～80个特征值时去噪重构效果最佳。对3类稀疏变换进行验证和仿真，得到3类稀疏变换对原始图像和高斯噪声图像的去噪效果对比结果，分别如图2、3所示。

从视觉效果的角度来看，3类稀疏算法的去噪效果大致一样，与受高斯噪声污染的噪声图像相比(图1、2)，在细节表现方面都比较清晰，噪声点减少，失真度较小，但都不可避免地存在高斯噪声叠加后留下的高灰度值，即雪花式斑点。

在放大去噪图像后可以看出，DCT去噪算法损失了一些关键性的细节，图像边缘存在较多明显锯齿状的像素块，如图2(b)中Cameraman的面部和相机轮廓都有一定的模糊化，远处的背景建筑物边缘失光。而经SVD算法处理后的噪声图像，锯齿状的边缘较少，画面较为平滑，物体的边缘轮廓特征较好地保留下来，在这方面比DCT算法更优，但是噪点却是3类稀疏算法中最多的，其原因是特征值的选取受主观因素影响较严重，需要进一步研究在不同噪声和图像的情况下，最优特征值的取值范围。DWT去噪是通过非线性的高、低通滤波器来完成稀疏分解的，由图2(c)可知，该算法的去噪性能在视觉上的效果是最好的，噪声点受到了较为强烈地抑制，基本上退化了噪声图像。

由图3可以看出，通过DCT、DWT、SVD算法去除噪声后，大幅度缩小了与原始图像之差。DCT和DWT剩余的噪声信号大部分集中在图像内部的轮廓边缘上，使得高频分量(细节系数)仍然携带着高斯噪声信息。SVD则是均匀分布在整幅图片上，因此验证了上述所提到的SVD算法可以保留图像轮廓特征信息的想法。

(a)原始图像(b)离散余弦变换后的图像(c)离散小波变换后的图像(d)奇异值分解后的图像图2 3类稀疏变换对原始图像的去噪效果对比(标准差σ=10)

(a)高斯噪声图像(b)离散余弦变换后的图像(c)离散小波变换后的图像(d)奇异值分解后的图像图3 3类稀疏变换对高斯噪声图像的去噪效果对比(标准差σ=10)

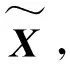
MSE评价指标反映的是去噪图像与原始图像之间的差异程度，差异越大，去噪效果越差，而PSNR表示图像的失真程度，其数值越大，图像失真越小。通过对比分析表1中的数据，可以发现，随着标准偏差σ值的增加，即噪声的不断加强，均方误差也随之增大，两者呈线性相关，从一定程度上表明了，当图像中的高斯噪声点过多，稀疏算法去噪的效果也不明显，因此图像的噪声退化程度具有广义上的局限性。 在标准偏差较小的场合时， SVD算法的MSE值是相对较小的，次之则是DWT，最次为DCT。从表1可以直观地看出，DCT算法对高斯噪声的敏感度不大， 所以在σ值较大时， MSE值的增幅反而是最小的，次之为DWT，最后是SVD算法。这3类稀疏去噪算法中，DWT的运行时间最短。

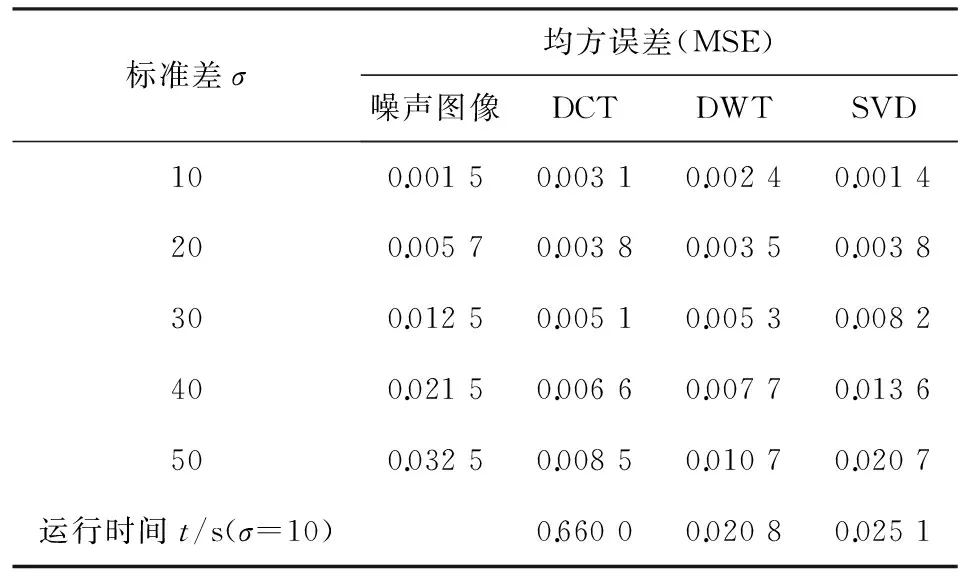
表1 3类稀疏算法去噪效果的均方误差值

注：1)DCT表示离散余弦变换；2)DWT表示离散小波变换；3)SVD表示奇异值分解。

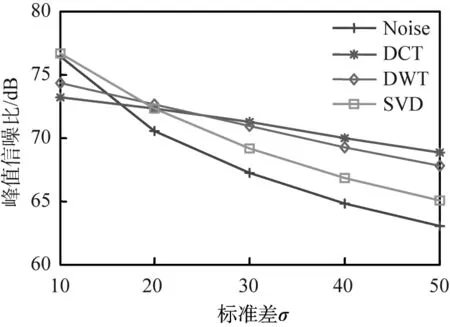
Noise—噪声图像；DCT—离散余弦变换；DWT—离散小波变换；SVD—奇异值分解。图4 3类稀疏算法去噪效果的峰值信噪比

根据图4可知，在高斯噪声的标准偏差较小时(σ=10)，得到的PSNR值与人眼观察到的图像质量不一致，即噪声图像的失真程度反而比去噪后的更小，如此并不符合人类视觉的特性。不过，当图像添加的噪声偏差较大时，PSNR指标没有出现奇异值。综上所述，PSNR对亮度变化差异较大时敏感度较强，并且图像失真程度随着σ的增大，其值呈现逐渐减缓的趋势，直至达到最小边界值。

通过DCT、DWT、SVD算法重构去除噪声后得到的图像分别如图5—7所示。分析可知：DCT变换的特点是去噪后的图像大部分的能量通常集中在低频部分；DWT变换可以比较好地对噪声进行抑制，而且还较好地对图像的细节进行了保护；SVD算法去噪后的效果比较符合视觉感官，去噪效果也较好。

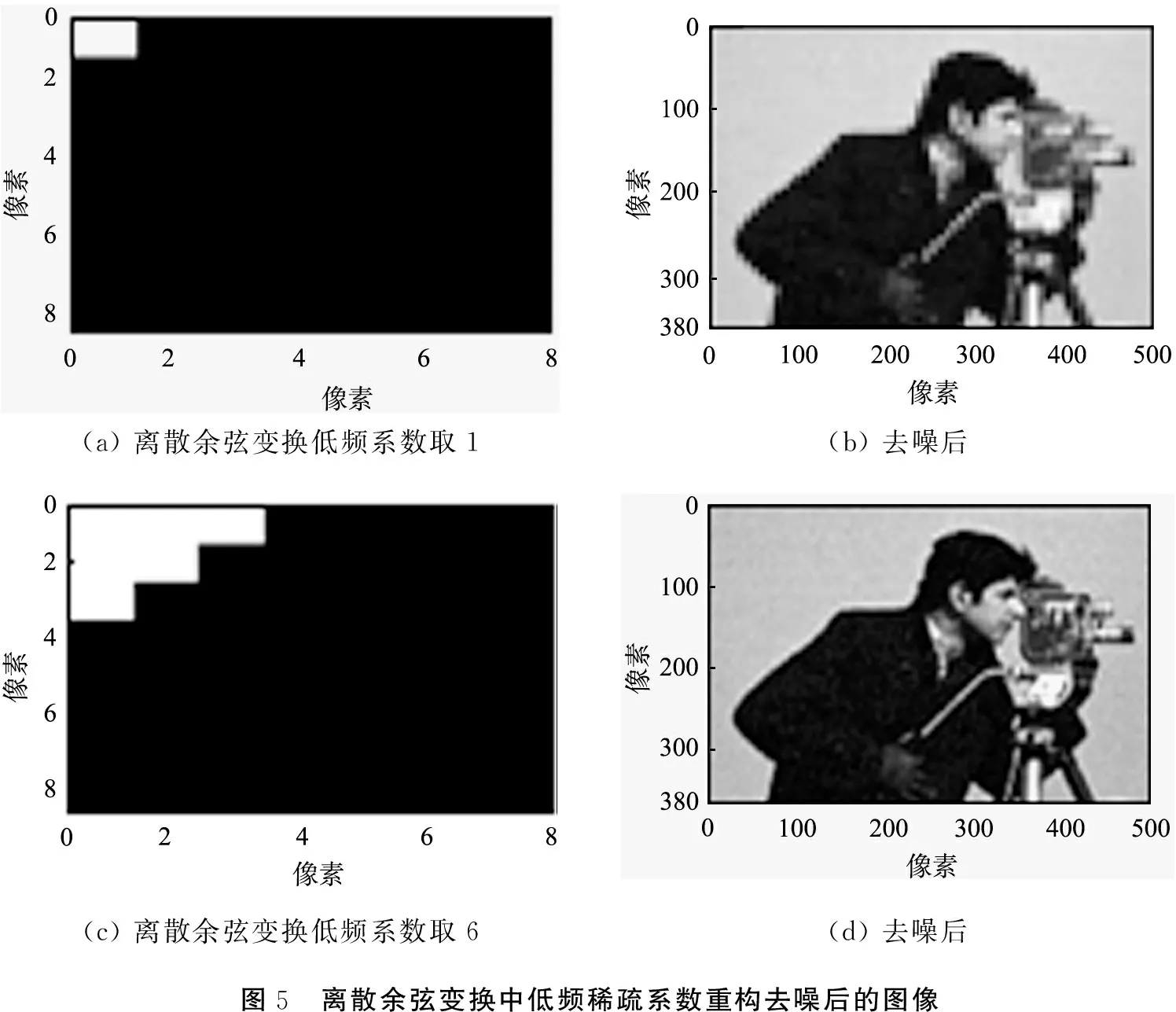
(a)离散余弦变换低频系数取1(b)去噪后(c)离散余弦变换低频系数取6(d)去噪后图5 离散余弦变换中低频稀疏系数重构去噪后的图像

(a)小波稀疏分解(b)去噪后图6 离散小波变换分解与重构去噪后图像

(a)噪声图像 (b)1个特征值重构(c)30个特征值重构 (d)70个特征值重构图7 奇异值分解特征值重构图像

3 结论

通过对3类稀疏表示的去噪性能进行了仿真对比实验，综合主观视觉与客观指标评价方法，得到以下结论：稀疏表示的去噪算法对高斯噪声具有明显的削弱作用，可以有效地退化噪声图像，同时去噪后的图像均方误差小，失真程度低。其中，DCT与DWT算法具有低灵敏度、去噪性能稳定的性质，SVD算法在σ=20之前的去噪图像失真程度最小。

[1] 王保宪,唐林波,陈聪葱,等. 基于圆形采样和稀疏表示模型的鲁棒目标跟踪[J]. 北京理工大学学报, 2016, 36(9)：983-990.

[2] 马晓，张番栋，封举富.基于深度学习特征的稀疏表示的人脸识别方法[J]. 智能系统学报，2016, 11(3): 279-286.

[3] 高红霞, 吴丽璇, 徐寒, 等. 微焦点X射线图像乘性加性混合噪声的去除[J]. 光学精密工程, 2014, 22(11): 3100-3113.

[4] 王智文，李绍滋.基于多元统计模型的分形小波自适应图像去噪[J]. 计算机学报, 2014, 37(6): 1380-1389.

[5] 汪春霆, 李修国, 王爱华. 基于FPGA的高精度高斯白噪声产生方法[J]. 北京理工大学学报, 2010, 30(4): 474-477.

[6] 石光明, 刘丹华, 高大化, 等. 压缩感知理论及其研究进展[J]. 电子学报, 2009, 37(5): 1070-1081.

[7] 陈伟，蔡占川，齐东旭. 一类新的正交矩-Franklin矩及其图像表达[J]. 计算机学报, 2015, 38(6): 1140-1147.

[8] 牟世刚, 冯显英, 晏志文, 等. 基于小波分析的动平衡机不平衡量提取方法研究[J]. 山东大学学报(工学版), 2011, 41(3): 62-66.

[9] 田伟, 乔谊正, 马志强. 基于DWT的二次特征提取脱机中文签名鉴定[J]. 山东大学学报(工学版), 2007，37(3): 55-59.

[10] 彭玉楼, 何怡刚, 林斌. 基于奇异值分解的压缩感知噪声信号重构算法[J]. 仪器仪表学报, 2012, 33(12): 2655-2660.

[11] 陈大伟, 闫昭, 刘昊岩. SVD系列算法在评分预测中的过拟合现象[J]. 山东大学学报(工学版), 2014, 44(3): 15-21.

[12] 李恒建, 张家树, 陈怀新. 基于稀疏模型的Bandelet图像去噪方法[J]. 铁道学报, 2010, 32(5): 108-113.

[13] 王敏,周磊,周树道,等. 基于峰值信噪比和小波方向特性的图像奇异值去噪技术[J]. 应用光学, 2013, 34(1): 85-89.

[14] 穆峰, 常发亮, 蒋沁宇. 基于改进EMD算法的信号滤波[J]. 山东大学学报(工学版), 2015, 45(3): 5-42.

[15] 徐凌伟, 张浩, GULLIVER T A.TAS/SEC系统在N-Nakagami信道下的性能分析[J]. 山东大学学报(工学版), 2015, 45(4): 84-90.