连续刚构桥悬臂施工合龙误差风险分析

谢逸超 张智超 徐旗强

(1.宜昌市夷陵区公路管理局 宜昌 443100； 2.湖北三峡职业技术学院 宜昌 443100)3.中国公路工程咨询有限公司 北京 100032)

随着对桥梁工程风险分析研究的不断深入，桥梁工程领域中的风险概率估计的方法也越来越多，因此，综合利用已有研究成果，有效消除不确定性，建立准确度高、实用性强的桥梁工程风险概率估计方法具有重要研究意义。本文以大跨径预应力混凝土连续刚构桥为主要研究对象，以百岁溪大桥悬臂浇筑施工为依托，参考借鉴已有桥梁风险分析理论和方法，应用基于BP神经网络和蒙特卡罗原理的风险概率估计方法，对该桥悬臂浇筑施工中跨合龙误差风险进行分析。

1 基于BP神经网络-蒙特卡罗原理的风险概率估计方法

1.1 桥梁悬臂施工风险概率定义

桥梁工程中风险概率[1]模型可定义为描述桥梁结构或者构件风险损失现实发生可能性的数学描述。设桥梁结构或构件在风险事态A情况下，其效应值为S，结构或者构件的抗力值为R。设风险事态A在区间[A1,A2]时，结构或者构件失效，其损失发生概率可表示为

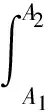
(1)

将式(1)离散化，可得

(2)

由式(2)可见，对于桥梁工程，若要准确计算具体风险损失的风险概率模型，既要确定只与风险事态本身属性有关的风险事态出现概率，也要确定与风险事态本身属性、桥梁结构特性等均有关的风险事态引起桥梁损失发生的概率。对于风险事态引起桥梁损失的概率，往往是通过建立极限状态方程，用失效概率近似代替风险概率。

1.2 桥梁悬臂浇筑施工风险概率计算模型

桥梁悬臂浇筑施工过程中，损失现实发生与风险事态之间的关系十分复杂，即一种风险事态发生后可能引起多起风险损失，而一种风险损失的产生也可能是由多种风险事态共同作用的结果。桥梁悬臂浇筑施工过程中，具体风险损失的概率函数一般是非线性、非显示表达式[2]。为研究此类风险概率的计算，本文综合运用有限元分析、正交试验设计、BP神经网络以及蒙特卡罗等相关原理对桥梁施工过程中具体的风险事件发生的概率进行求解，具体计算流程见图1。

图1 风险概率估计流程图

2 百岁溪大桥中跨合龙误差风险分析

2.1 百岁溪大桥概况及悬臂施工模型

百岁溪大桥位于湖北省宜昌市，大桥全长368 m，为95 m+170 m+95 m连续刚构桥，主梁为单箱单室三向预应力箱梁，箱梁顶宽10 m、底宽5.5 m，悬臂长2.25 m。梁高从墩顶的10.0 m向跨中的3.8 m以二次抛物线过渡。

采用midas Civil建立百岁溪大桥悬臂浇筑施工仿真模型，模拟该桥悬臂浇筑施工过程，主梁为C50混凝土，主墩为C40混凝土，纵向预应力为фs15.2-19钢绞线。根据现场实际情况，将模型划分为76个施工阶段，着重分析中跨合龙阶段(70号施工阶段)的合龙挠度误差。

2.2 百岁溪大桥中跨合龙误差风险概率估计

根据文献[3]，将主梁混凝土容重、主梁混凝土弹性模量、预应力钢束张拉控制误差、挂篮荷载误差及两悬臂施工进度误差(主梁混凝土收缩徐变的影响)作为研究百岁溪大桥悬臂浇筑施工中跨合龙挠度误差的主要控制参数。其中，将挂篮荷载误差进一步细化为挂篮重量误差和挂篮偏移误差。各随机变量的分布类型及变异系数(标准差)部分参考GB/T50283-1999 《公路工程结构可靠度设计统一标准》、JTG/T F50-2011 《公路桥涵施工技术规范》、JTJ04-2000 《公路钢筋混凝土及预应力桥涵设计规范》关于各参数误差允许的规定以及文献[4-5]确定，见表1。

表1 基本随机变量统计特征及随机变量水平值

对百岁溪大桥中跨合龙准备阶段(即70号施工阶段)的合龙挠度误差进行风险分析，根据前文主要控制参数建立风险临界状态函数

g(x)=δr(Er，rr，F1r，F2r，Dr，Zr)-

δl(El，rl，F1l，F2l，Dl，Zl)

(3)

式中：δr，δl为两悬臂端中跨合龙准备阶段的挠度值;E，r，F1，F2，D，Z为各悬臂端所对应的控制参数值。

根据临界状态方程及各控制参数所服从的分布规律，利用等水平正交试验设计方法，按照6因数5水平的正交试验设计表生成25个BP神经网络训练输入样本(各参数水平值见表1)，并将输入样本代入已建立的百岁溪大桥悬臂浇筑施工分析模型，求得中跨合龙阶段的合龙挠度值作为输出样本。其中，随机取5个样本作为检验样本。利用MATLAB软件建立BP神经网络模型，输入个数为6，输出个数为1，隐层节点数取16个。模型训练至42 919步时，误差满足要求，并且最终形成收敛水平曲线，停止训练。图2为百岁溪大桥中跨合龙挠度有限元计算输出与BP神经网络训练输出和BP神经网络检验输出对比图。

图2 有限元计算值与BP神经网络输出值对比图

由图2可见，网络训练效果比较好。因此，该BP神经网络模型可近似替代百岁溪大桥在70号阶段的最大悬臂端累计位移与基本随机变量的映射关系。

在建立百岁溪大桥悬臂浇筑施工中跨合龙挠度与随机变量之间映射关系的BP神经网络后，根据蒙特卡罗模拟原理，按照前面建立的临界状态函数，分别计算该桥中跨合龙时，两悬臂挠度误差大于20，30，50 mm的风险概率。

利用MATALAB软件自带随机数生成器，按照各控制因素所服从的分布规律随机生成2组输入样本，分别模拟该桥两悬臂施工中各控制参数值，每组N个仿真样本。将2组输入样本代入训练好的BP神经网络进行仿真计算，模拟该桥中跨合龙时的悬臂端挠度值。并随机从2组数中各取出一个求差值，设差值的绝对值大于临界值的次数为n，则风险发生的概率可以定义为

(4)

计算得出，百岁溪大桥悬臂浇筑施工中跨合龙挠度误差大于20 mm的风险概率为14.25%，大于30 mm的风险概率为2.63%，大于50 mm的风险概率为0.0 017 148%。

2.3 百岁溪大桥中跨合龙误差风险分析

根据该桥中跨合龙挠度误差是否满足设计要求、是否可以直接合龙(施工损失)、合龙后是否对结构后期运营有较大损伤(结构损伤)，对合龙挠度误差所引起的损失划分损失等级，并进一步列出该桥中跨合龙挠度误差风险评价，结果见表2。

表2 百岁溪大桥中跨合龙挠度误差风险评价表

3 结论

1) 综合运用有限元软件、正交试验设计、BP神经网络以及蒙特卡罗等相关原理，对桥梁施工过程中具体的风险事件发生概率进行求解的方法切实可行。

2) 百岁溪大桥悬臂浇筑施工中，主梁C50混凝土弹性模量及容重、挂篮荷载重量及偏移距离、预应力束张拉控制力、施工阶段持续时间在容许的范围内变动时，中跨合拢挠度误差不满足设计要求的风险概率为14.25%，施工中应重视对该桥悬臂浇筑过程线形的监控。

3) 本次分析未考虑预拱度设置、立模标高误差、前期施工状态、人为因素及合龙环境等对中跨合龙挠度误差的影响，实际施工中出现挠度误差风险损失等级为3、4级的风险概率应比计算结果更大。

[1] 阮欣，陈艾荣，石雪飞.桥梁工程风险评估[M].北京：人民交通出版社，2010.

[2] GUO X, GUO Y. Probability of collapse of a bridge system under seismic and scour hazards[J]. Proceedings of the Institution of Mechanical Engineers Part O Journal of Risk & Reliability,2016,230(2):195-203.

[3] 王永宽.大跨度连续刚构桥施工控制误差风险性分析[D].西安：长安大学,2011.

[4] 张杰.大跨度桥梁施工期风险分析方法研究[D].上海：同济大学，2007.

[5] 唐小兵,贾志伟,黄爱,等.连续刚构桥施工过程中腹板斜裂缝成因分析及试验研究[J].武汉理工大学学报(交通科学与工程版),2017,41(2):195-198.