采用改进的LQR进行Pendubot系统的平衡控制

， ，，，

(东北大学机械工程与自动化学院，辽宁 沈阳110819)

0 引言

Pendubot是一种典型的欠驱动非稳定机器人[1]，由两个机械臂组成，第一个机械臂(肩部关节)由电机驱动，为主动机械臂，第二个机械臂(肘部关节)可以自由活动，为欠驱动臂。Pendubot可以作为欠驱动基准系统，用于验证各种非线性控制算法。Pendubot系统的控制分为摇起控制和平衡控制两部分。摇起控制是从稳定的下垂位置(Down-Down)运动到最高不稳定平衡位置(Up-Up)；平衡控制是使系统稳定在最高不稳定平衡位置。通常，摇起控制和平衡控制分别设计，并通过控制转换装置进行切换。

早在1995年美国的Spong等就对Pendubot系统的可控性进行了证明[2]。Pendubot系统的摇起控制主要方法主要有部分反馈线性化方法[2]、能量控制方法[3-4]、混杂控制方法[5]、滑膜控制方法[6-7]和智能控制方法[8]等；平衡控制的主要方法有线性二次型调节器(LQR)[2]、极点配置法、模糊控制[9-10]、角动量控制[11]和神经网络控制[12]等。在Pendubot系统的控制中，LQR控制器是应用最广泛的平衡控制器。在已有的文献中，采用LQR控制器进行Pendubot系统的平衡控制时，两个机械臂均处于竖直位置，平衡状态下主动臂的力矩为0。对Pendubot系统处于非最高不稳定平衡位置时的平衡控制进行研究，平衡状态下主动臂的力矩不为0。在详细分析Pendubot系统的动力学方程的基础上，对LQR控制器进行了改进。建立Pendubot系统的仿真模型，对该方法进行了验证。

1 Pendubot系统的动力学模型

通过拉格朗日方程来建立Pendubot系统的动力学模型(不考虑摩擦力的影响)为:

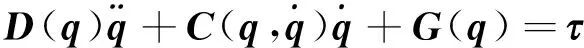
(1)

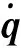
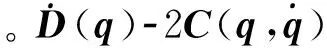
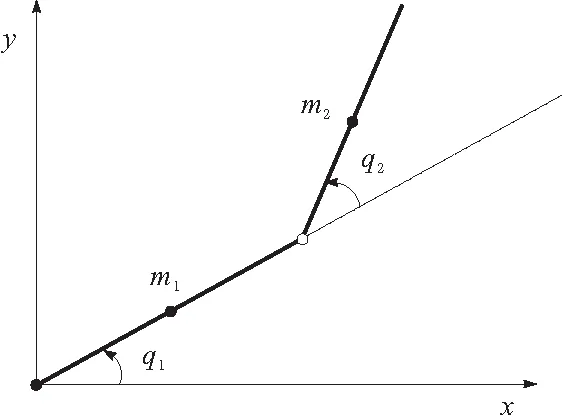
图1 Pendubot系统的模型

在图1中，m1和m2分别表示主动臂和欠驱动臂的质量，q1表示主动臂相对于坐标轴x的夹角，q2表示欠驱动臂相对于主动臂的夹角，l1和l2分别表示主动臂和欠驱动臂的长度，lc1和lc2分别表示主动臂和欠驱动臂相对于质心的距离，I1和I2分别表示主动臂和欠驱动臂的转动惯量。下面将Pendubot系统的动力学方程中的参数变为以下的5个新参数。

(2)

将式(2)中的参数带入到Pendubot系统的动力学方程中，可以得到

(3)

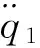
(4)

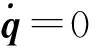
(5)

假设τ1/θ4g≤1，可以求解出q1和q2为：

其中n=1,3,5,…

(6)

(7)

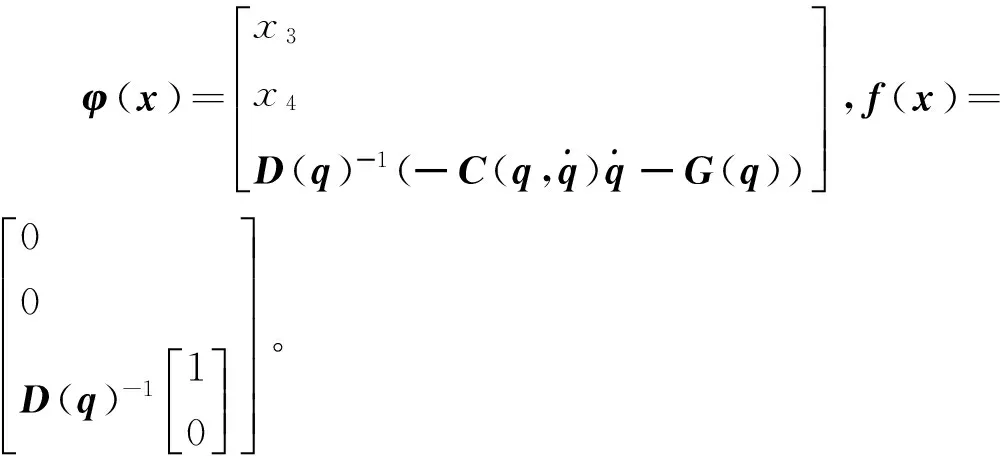
(8)

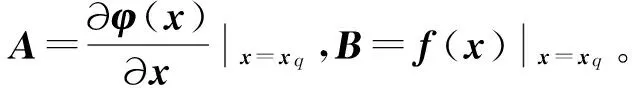
2 LQR控制器

线性二次型调节器(LQR)属于现代控制理论，其性能指标易于分析、处理和计算，并具有很好的鲁棒性。LQR的目的是在一定的性能指标下，使系统的控制效果最佳，即利用最少的控制量来达到最小的状态误差。根据Pendubot系统在平衡位置进行线性化后的状态方程，定义如下的性能指标

(9)

矩阵Q是正定或半正定实对称矩阵，即Q≥0，矩阵R是正定实对称矩阵，即R>0。矩阵Q和R用来平衡状态变量和输入向量的权重。使 J达到最小值的最优控制律为：

τ1=-R-1BTPx= -Kx

(10)

其中，参数K=R-1BTP为最优状态反馈矩阵，参数P是下面Riccati方程的解。

ATP+PA-PBR-1BTP+Q=0

(11)

3 改进的LQR进行平衡控制

如果将Pendubot系统稳定在状态变量xi=[π/2 0 0 0]T的不稳定平衡位置，由于平衡状态下主动臂的驱动力矩为0，因此可以直接采用式(10)进行平衡控制。本文的控制目标是将Pendubot系统稳定在状态变量为xq=[3π/8 π/8 0 0]T的不稳定平衡位置，即主动臂的角度为3π/8，欠驱动臂为竖直位置。对于位置xq，由于驱动力矩大于0，不能直接采用式(10)进行平衡控制。为了使Pendubot系统稳定在平衡位置xq，需要对LQR控制器进行改进。

首先求解平衡位置xq处的状态反馈矩阵K。将状态变量xq带入到式(8)中，得到矩阵A和B分别为：

在MATLAB软件中采用函数lqr()进行LQR控制器的设计，该函数的调用格式为K=lqr(A,B,Q,R)，其中参数Q为4阶单位矩阵，参数R=1。在平衡位置xq，得到的状态反馈矩阵为K=[-71.22 -56.78 -12.76 -8.31]。

为了使Pendubot系统稳定在平衡位置xq，在式(10)中，将状态变量修改为xqΔ=[3π/8+Δπ/8-Δ0 0]T，即

τ1=-KxqΔ

(12)

参数Δ为补偿角度值。下面介绍如何求解Δ。

Pendubot系统处于平衡位置xq时，驱动力矩为恒定值，并满足式(5)，则驱动力矩为：

τ1=θ4gcos(q1)+θ5gcos(q1+q2)

=0.783 1 N·m

(13)

将力矩τ1，状态变量xqΔ和反馈矩阵K带入公式(12)，可以求得 Δ=0.054 3。

3 仿真分析

在仿真中采用的Pendubot系统[3]模型参数为θ1=0.030 8 kg·m2，θ2=0.010 6 kg·m2，θ3=0.009 5 kg·m2，θ4=0.208 6 kg·m，θ5=0.063 0 kg·m。

采用MATLAB/Simulink建立Pendubot的系统模型，系统的仿真时间为3 s，初始状态的状态变量为xi=[π/2 0 0 0]T，仿真步长为1 ms。

将Pendubot系统从初始状态稳定到状态变量为xq=[3π/8 π/8 0 0]T的不稳定平衡位置。采用LQR控制器和改进的LQR控制器的结果如图2和图3所示。在图2中，采用LQR控制器时，系统稳定时主动臂的角度q1=1.226 0，大于设定的角度值3π/8；欠驱动臂的角度q2=0.344 8，小于设定的角度值π/8。采用改进的LQR控制器时，系统稳定时主动臂的角度q1=3π/8，欠驱动臂的角度为q2=π/8，即稳定在位置xq。

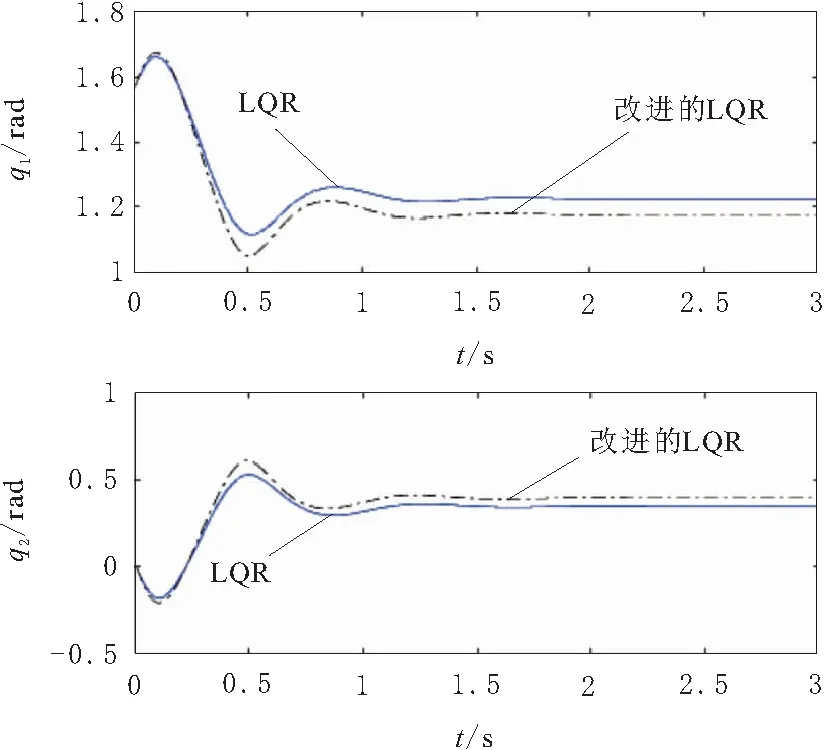
图2 Pendubot系统的输出角度

在图3中，采用LQR控制器时，稳定状态下的驱动力矩为0.691 7 N·m；采用改进的LQR控制器时，稳定状态下的驱动力矩为0.783 1 N·m，和式(13)的计算值相等。采用LQR控制器和改进的LQR控制器都能使Pendubot系统稳定。直接采用LQR控制器时，Pendubot系统并没有稳定在设置的平衡位置xq，但是改进的LQR控制器能够使系统稳定在设置的位置xq。

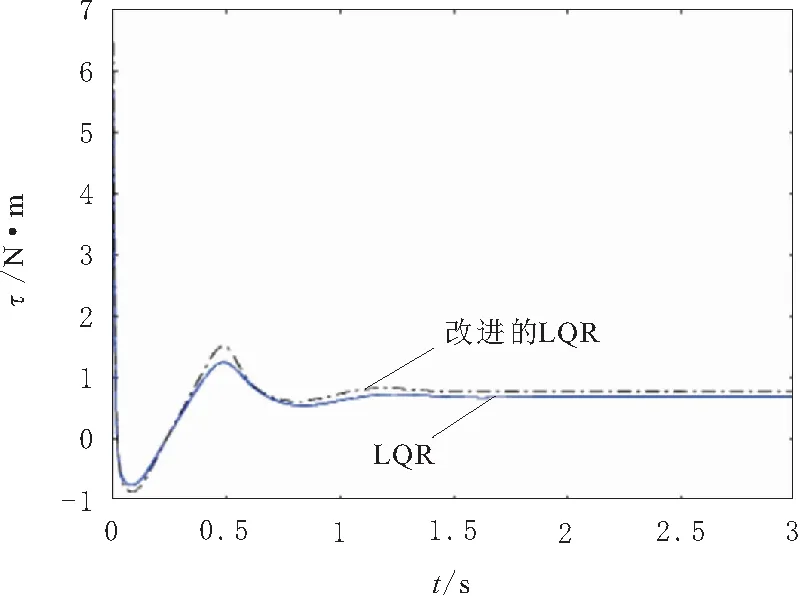
图3 输入力矩

4 结束语

在利用LQR进行Pendubot系统的平衡控制中，当主动臂和欠驱动臂都处于竖直位置时，在稳定状态下主动臂的输入力矩为0，可以直接采用LQR进行平衡控制。利用LQR对Pendubot系统的平衡位置进行控制时，主动臂不在竖直位置，只有欠驱动臂在竖直位置。如果直接采用LQR进行控制，由于平衡位置的力矩大于0，Pendubot系统并不能稳定在设置的位置。根据设定的平衡位置，以及平衡位置处的力矩值，设计了一个补偿参数，并给出了补偿参数的详细计算方法。通过改进的LQR控制器，使得Pendubot系统能够稳定在设置的平衡位置。

[1] LIU Y, YU H. A survey of underactuated mechanical systems[J]. IET Control Theory and Applications, 2013, 7(7):1-15.

[2] SPONG M W, BLOCK D J. The pendubot: a mechatronic system for control research and education[C]//Proceedings of the 34th Conference on Decision & Control, 1995, 555-556.

[3] FANTONI I, LOAZNO R, SPONG M W. Energy based control of the pendubot[J]. IEEE Transactions on Automatic Control, 2000, 45(4):725-729.

[4] XIN X, TANAKA S, SHE J, et al. New analytical results of energy-based swing-up control for the Pendubot [J]. International Journal of Non-linear Mechanics, 2013, 52(3):110-118.

[5] ZHANG M, TARN T J. Hybrid control of the pendubot[J]. IEEE/ASME Transactions on Mechatronics, 2002, 7(1):79-86.

[6] 王伟，易建强，赵冬斌,等. Pendubot的一种分层滑膜控制方法[J]. 控制理论与应用, 2005, 22(3):417-422.

[7] 牛瑞燕，许午啸，刘金琨. 欠驱动机械臂滑膜控制与实验研究[J]. 仪器仪表学报, 2016, 37(2):348-355.

[8] EOM M, CHEA D. Robust swing-up and balancing control using a nonlinear disturbance observer for the pendubot system with dynamic friction[J]. IEEE Trans. Robotics, 2015, 31(2):331-343.

[9] LI W, TANAKA K, WANG H O. Acrobatic control of a Pendubot[J]. IEEE Transactions on Fuzzy Systems, 2004, 12(4):549-552.

[10] Sanchez E, Flores V. Real-time underactuated robot swing-up via fuzzy PI+PD control[J]. Journal of Intelligent & Fuzzy Systems, 2006, 17(1):1-13.

[11] AZAD M, FEATHERSTONE R. Angular momentum based balance controller for an under-actuated planar robot [J]. Autonomous Robots, 2015, 40(1):1-15.

[12] XIA D, WANG L, CHAI T. Neural-network-friction compensation based energy swing-up control of Pendubot[J]. IEEE Transactions on Industrial Electronics, 2014, 61(3):1411-1423.