多阵面天线运动控制的实现

，

(成都天奥测控技术有限公司，四川 成都 611731 )

0 引言

卫星通信具有通信距离远、覆盖范围大、通信方式灵活多样、质量高、不受地理和自然环境限制等一系列的优点，随着全球经济和信息化的飞速发展，越来越多的信息通过卫星进行传输，在移动载体上进行卫星通信已经成为实时通信的迫切需求，因此移动载体卫星通信必将是卫星通信的一个发展趋势。按照载体的类型不同分为车载卫星通信平台，机载卫星通信平台和船载卫星通信平台三大类[1-2]。由于机载设备特别是舱外设备需具备重量轻、迎风面小、响应快等要求，为此本文提出了一种具有低剖面、多轴联动控制的平板阵列动中通天线，其优点是轮廓低，射频集成化高，可实现收发共用[2]。现在主要适用于大型飞机上，填补国内空白，具有广阔的应用前景。

1 基本原理

低剖面动中通天线多轴控制系统基于机载稳定平台控制原理，使用3个天线阵面朝同一方向，并且阵面的正上方不得相互遮挡。采用3轴联动控制，可实现方位和俯仰两个方向的旋转运动，以及阵面的直线运动。运用2个单轴速度陀螺进行稳定控制，通过坐标转换将载体的姿态信息转换到方位和俯仰2个运动控制轴上，同时直线运动机构根据俯仰的运动角度进行横向运动，实现3个天线阵面互不遮挡且在整个运动过程中法向面面积始终保持不变。阵面原理如图1所示。

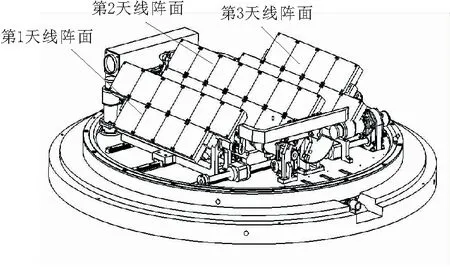
图1 天线阵面原理图

2 控制策略

2.1 总体控制策略

低剖面动中通天线多轴运动控制系统具有捕获和跟踪两种模式。捕获时，根据目标姿态值信息快速运动到相应位置。为了达到系统的响应要求和控制精度，采用了速度前馈补偿控制策略。捕获完成时系统迅速转入到跟踪模式，采用速度陀螺作为稳定环路进行稳定控制。本控制系统采用共轴跟踪控制原理[3-5]，它的特点是通过引入惯性角位置反馈信号(载体导航信息)构成独立的位置回路，旋转变压器、跟踪控制算法等控制指令结算环节与随动控制系统分离，从而使控制系统摆脱了滞后等因素的带宽限制。该系统采用载体的GPS信息及辅助惯性导航信息作为基准姿态信息，它构成了位置反馈的主回路，同时在接收基准姿态信息的间隔内，采用速度陀螺作为稳定回路，其控制原理图如图2所示。

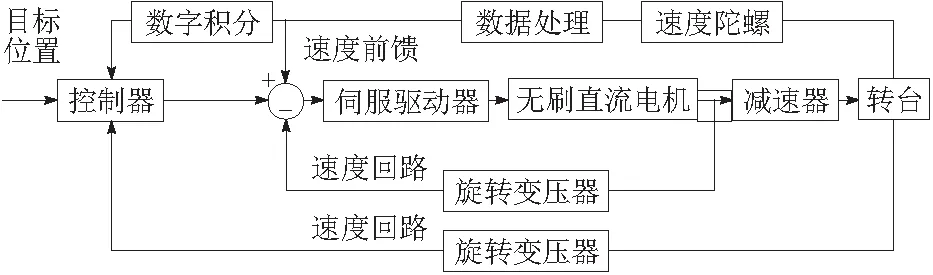
图2 控制系统原理

2.2 直线同步跟踪控制

为了实现在整个过程中3个阵面互不遮挡，左右两边的阵面在转动的过程中还需要分别向左右进行直线运动，运动的位移有阵面转动的角度决定，如图3所示。根据图3可得：

(1)

其中L为阵面的宽度，并与L1相等。

则移动的位移为：

S=L2-L1

(2)

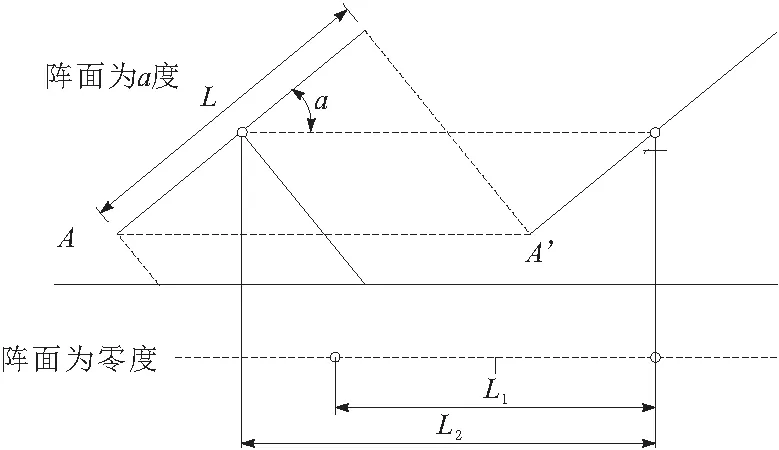
图3 阵面变换

由于直线运动与阵面的俯仰运动存在同步控制关系，实现同步控制的策略有以下几种：

主从同步控制，该方法采用俯仰轴为主动轴，直线运动轴根据俯仰轴反馈的角度进行实时计算后，跟随俯仰轴运动；缺点是受俯仰轴控制精度的影响，同时存在较大的滞后；

虚拟轴同步控制，该方法是建立一个虚拟运动轴，俯仰轴和直线轴同时去跟随虚拟轴，但是系统的跟随精度在同步运动的过程中不能受控；

主从控制补偿控制，该方法是主从控制的优化控制，在主从控制的基础上，根据两轴的反馈值进行实时补偿，以达到同步跟踪的更高精度控制。该方法跟随精度高，跟随性能好，弥补前两种控制策略的不足，但是控制策略较复杂。

由于本系统需要俯仰控制的精度高动态响应快，同时直线运动的精度要求相当较低，防止俯仰轴反馈角度对直线的影响，因此采用虚拟轴同步控制策略。

3 系统的隔离控制原理

对载体(基座)外界干扰进行隔离，主要采用惯导系统实现，目前比较主流的方式有两种，一是将三轴陀螺安装在载体上，陀螺能够敏感的感知载体的姿态变化，但是由于需要将载体的姿态转换到天线阵面坐标系下，转换存在较复杂的非线性模型。第二种方式是将二自由度的陀螺安装在俯仰天线阵面上，一轴垂直于阵面，一轴平行于阵面转动轴[6-7]，如图4所示。

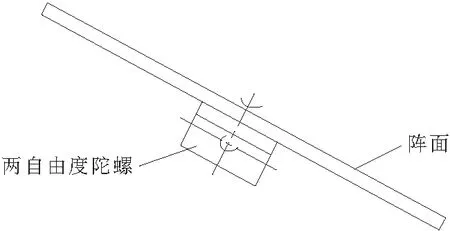
图4 陀螺安装

根据陀螺的安装方式首先设定基座的所在坐标系为b系，根据坐标系变换将b系转换到天线阵面坐标系(设定为f系)。首先坐标系绕b系的Z轴(即垂直于基座平面的轴)转动θa角度，记为a系；然后以a系为基准绕X轴(即俯仰方向)转动θf度，记为f系，a系和b系的相对位置如图5所示，f系和a系的相对位置如图6所示。

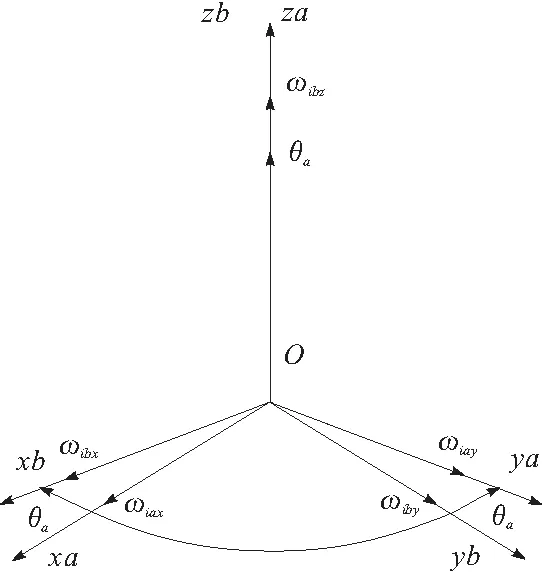
图5 a系和b系的相对位置

图6 f系和a系的相对位置

设定ωibx，ωiby，ωibz为载体(基座)沿3个坐标轴的角速度分量，根据坐标转换的公式进行运算[8-9]，a系的坐标转换结果为:

(3)

f系的坐标转换结果为:

(4)

f系的角速度等于由载体角速度和方位、俯仰伺服回路角速度的叠加为：

(5)

按照天线稳定系统的要求计算得：

(6)

(7)

ωifx由俯仰陀螺测得，此处俯仰陀螺轴线平行OXf轴；ωifz由方位陀螺测得，此处俯仰陀螺轴线平行OZf轴。

4 系统控制仿真分析

4.1 仿真模型的建立

根据本系统的控制策略，建立控制系统的仿真模型，主要包括伺服电机数学模型、控制策略数学模型和稳定控制模型。首先根据功能要求进入捕获模式，当捕获完成后系统立即切换到跟踪模式。在跟踪模式下，速度陀螺在时间间隔内进行位置积分，然后将积分值经坐标系变换后与给定目标值进行数据叠加，其仿真框图如图7所示。

其中伺服电机的仿真模型包括电机数学模型、电流环控制、速度环控制、反电动势、转矩系数和转速输出[10]，如图8所示。

4.2 仿真模型分析

根据动中通天线的相关技术要求，天线指向角速度最大值：方位≥90°/s，俯仰≥30°/s；天线指向角加速度：方位≥25°/s2，俯仰≥60°/s2。因此将方位拟合成振幅324°，周期为22.4 s的正弦曲线；俯仰振幅15°，周期为3.14 s的正弦曲线进行仿真，其仿真结果如图9、图10所示。

经过仿真分析，采用传统PID控制动态响应不够，导致系统跟踪误差不能达到要求，其跟踪精度都高达0.4°以上，而采用了传统PID控制与速度前馈补偿相结合的控制策略大大提高了动态响应性能，方位跟踪精度达到0.2°，俯仰跟踪精度达到0.28°。

图7 控制系统模型

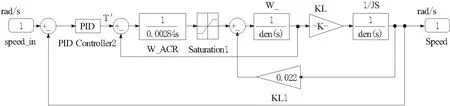
图8 伺服电机模型

图10 俯仰跟踪误差

5 测试结果

为了验证本控制系统的控制效果，在实验室里将天线安装在转台上，通过转台的运动来改变天线的姿态，分别进行了静态控制和动态跟踪测试，其结果如表1所示。

表1 系统控制精度

6 结束语

低剖面动中通天线控制系统的跟踪精度直接影响通信质量，为了抑制因控制精度而引起的与卫星通信信号的衰减量，详细分析了控制系统的控制策略，在传统PI控制策略的基础上，引入了速度前馈补偿和同步控制策略，达到了较高的跟踪精度。同时采用二轴速率陀螺的稳定控制策略，避免了因引入传统三轴速度陀螺进行复杂的坐标变换而引起的非线性耦合误差。通过仿真和实际测试表明，该控制系统达到了机载动中通天线的静态精度和动态跟踪要求。

[1] 陈健明.船载卫星天线自动跟踪技术研究与实现[J].大连理工大学学报，2009，1:1-3.

[2] 牛传峰，杜彪，韩国栋,等. 低轮廓动中通天线[J].中国电子科学研究院学报，2013,8(2)：149-155.

[3] 黄一，吕俊芳，卢广山. 机载光电跟瞄平台稳定与跟踪控制方法研究[J].飞机设计，2003(3):38-42.

[4] 李富贵，夏群利,蔡春涛，等. 导引头隔离度对寄生回路稳定性的影响[J].红外与激光工程，2013,42(9)：2341-2347.

[5] 刘晓军.稳定跟踪平台移动载体姿态测试技术与建模[D].长沙：国防科技大学，2005.

[6] 杨蒲，李奇.基于滑模变结构的陀螺稳定平台非线性解耦控制[J].仪器仪表学报，2008,29(4)：771-776.

[7] 原晓刚，吴旭光，宁腾飞. 稳定平台设计与控制[J].国外电子测量技术，2012,31(9)：41-42.

[8] 李少伟，施朝健，黄震民. 船载稳定水平平台系统[J].电子测量技术与仪器学报，2007,30(6)：192-194.

[9] 杨蒲，李奇. 三轴陀螺稳定平台控制系统设计与实现[J].中国惯性学报，2007,15(2)：171-176.

[10] 张佳阳，高海涛，郑立熹.直流伺服电机拖动系统的仿真研究[J]. 中国制造业信息化,2009,38(15):44-50.