基于嵌入冗余信息方式的图像加密方案与实现
2018-03-07杨刘洋刘梦梦楼梦佳罗云秀吴仁红
吕 翔, 杨刘洋,, 刘梦梦, 楼梦佳, 罗云秀, 吴仁红
(1.浙江师范大学 数理与信息工程学院,浙江 金华 321004;2.重庆市潼南中学,重庆 402660;3.浙江师范大学 经济与管理学院,浙江 金华 321004)
0 引 言
在世界经济加速发展的当今,网络为经济建设提供了平台和技术支持.虽然网络通信可提供一些优质服务,但也会面临安全问题,比如:信息被修改、被拦截、被复制、被伪造、被恶意扩散等.针对这些问题,各国政府提出了多项保护性法律法规,并要求相关部门和运营商提供安全性更高的网络环境和技术支持.研究者为解决此类问题设计了多种信息隐藏、保护方面的应对方案.对数据量较大的图像类信息如何进行保护?各国学者也进行了大量的探索研究,已提出了多种各具优点的加密和保护方案.
比如,数字水印技术[1-6]就是一种应用于图像类信息的最典型、最常用的保护技术.该技术已在文艺领域、工业应用、国防科技等方面得到了大量的运用,起到了一定范围的防盗、维护版权作用.同时为了满足“绝密”的需要,也出现了只对特定对象才成“可视图像”的加密方案,比如文献[7-18]等.虽然近几十年来已经出现了大量的图像加密方案,但是总会存在一些缺点或漏洞.这就迫使人们需要不断努力地提出安全性更高、种类更多的图像加密方案,为网络通信提供保障.
很多以光学为手段的图像加密方案[7-9]对光学器件、物理环境要求较高;以混沌系统或超混沌系统为基础的图像加密方案[15-18],虽然在安全性方面有很大程度的提高(比如,可以抵抗统计和差分攻击),但是增加了计算的复杂性、计算量;以正交拉丁方为基础的图像置乱加密方案[10-11],虽然原理较简单,但是安全性不够高,尤其是对差分攻击的抵御能力非常弱.
为简化图像加密算法的复杂程度和提高算法抗攻击的能力,本文设计了一种基于嵌入冗余信息方式的图像加密方案,并进行了一定次数的加/解密仿真实验、抗攻击仿真实验及参数计算.
从所得仿真结果看,该算法不仅加/解密效果理想,而且还可以抵抗统计分析、差分分析、剪切攻击等多种外界攻击,表明本文提出的图像加密方法比文献[10-14]等的方法更加实用和有效.
1 嵌入冗余信息方式的图像加密算法
1.1 循环拉丁方与完备拉丁方的构造方案
定义1[12-14]若一个大小为n×n的数字矩阵A(n)=(aij)满足下列2个条件:
1)元素aij∈Sn=0,1,2,…,n-1(i,j∈Sn);
2)同行、同列元素互异;
则称该矩阵A(n)为一个n阶拉丁方.
定义2[12,14]若一个n阶拉丁方A(n)满足条件:相邻行、相邻列各元素组成的元素数对互异,则称该拉丁方A(n)为一个n阶完备拉丁方.
定义3[14]若一个n阶拉丁方A(n)满足条件:每行元素都是上一行元素依次向左循环移动k位而得,并且(n,k)=1(1≤k≤n-1),则称该拉丁方A(n)为一个n阶k循环拉丁方,记为Ak(n).
引理1[12,14]设n=2m为一个大于2的正偶数,若一个n阶拉丁方A(n)满足首行元素为0,1,2m-1,2m-2,3,2m-3,…,m-1,m+1,m,且其余各行均为前一行对应元素+1(modn)而得,并按照首行顺序进行换序,使得首列顺序与首行相同,则可得到一个n阶完备拉丁方B(n).
引理2[14]若设n阶不同拉丁方所具有的总数为L(n),则有L(n)≥(n!)2n/(nn)n.
由定义3可知,可以随意构造出一个A3(5)和一个A4(5),如下所示:

1.2 原始图像的预处理加密
在预处理加密阶段,为了满足不同大小图像的需要和像素在[0,255]之内取值,即可按照如下2种情况分别进行预处理.设有一个大小为n×n的256级原始灰度图O(n),则有[13]:
1)针对n≤256的情况:随意构造一个拉丁方A(n),并将其与图像O(n)按位进行异或运算实现预处理加密,即得加密图像M(n);
2)针对n>256的情况:先随意构造一个拉丁方A(n),再对其中大于等于256的元素进行连续取模直到所有元素均小于256为止,得到对应矩阵B(n),如
B(n)=A(n) (mod 256)
(1)
所示.最后将B(n)与图像O(n)按位进行异或运算实现预处理加密,即得加密图像M(n).由引理2和参考文献[14]可知,所有n阶不同拉丁方的总数量会随着阶数n的不同而具有指数级增长趋势,当阶数超过11时已经无法统计.因此,该方案可以有效抵抗枚举攻击.
1.3 预处理后的深度变换加密
为了进一步提高图像的安全性,常常需要对预处理后的图像作进一步深度变换加密处理.为了减少外界攻击干扰,设法将预处理图像随机地嵌入到一幅较大的噪声图像中,再利用完备拉丁方进行一定次数的空间坐标变换加密.嵌入后的图像对于预处理图像来说相当于增添了大量的冗余信息,经空间坐标变换后,一方面起到了隐藏有效信息的作用;另一方面还可以抵抗很多种外界攻击(比如差分攻击、剪切攻击等),从而为破解图像增加了难度.
深度变换处理步骤如下:
第1步,添加标记.
对预处理加密图像M(n)添加全“0”标记,分布在M(n)的首行和首列之前,使M(n)成为大小为(n+1)×(n+1)的标记图像C(n+1).
第2步,构造随机噪声图像.
随机构造一个大小为r×r的噪声图像D(r),要求r≥2n.
第3步,嵌入噪声图像.
将标记图像C(n+1)随机地嵌入到噪声图像D(r)中,替换D(r)中原来某一区域的噪声信息,即得冗余图像E(r).
第4步,空间坐标变换.
对冗余图像E(r)按照完备拉丁方变换矩阵H(r)的规律进行x次(x≥1)的空间坐标变换加密,即得最终加密图像F(r).
为满足不同大小图像加密的需要,下面分2种情况介绍完备拉丁方变换矩阵的生成方法[12].
1)r为偶数:
首先根据引理1的方法构造出一个r阶完备拉丁方W(r),然后将其扩展成具有r×r个互异数对的变换矩阵H(r).扩展规则:将前一列元素与后一列元素合并作为新的列数对,而最后一列元素重复合并后作为最后一列数对.例如:


2)r为奇数:
首先根据引理1的方法构造出一个(r-1)阶完备拉丁方W(r-1),然后加上一个相同阶数的全“1”矩阵,再扩展成具有r×r个互异数对的变换矩阵H(r).扩展规则:将前一列元素与后一列元素合并作为新的列数对,最后一列元素重复合并后作为最后一列数对,第一列元素s(1≤s≤r)扩展成首列数对(0,s),最后一行元素t(1≤t≤r)扩展成最后一行数对(t,0).例如:


1.4 基于嵌入冗余信息的图像加密算法设计
基于以上思想,笔者设计了如下加密算法:
第1步:读取原始灰度图像O(n);
第2步:计算O(n)的阶数n;
第3步:构造一个拉丁方A(n)或对应矩阵B(n),并将A(n)定为1级密钥;
第4步:将O(n)与A(n)或B(n)按位进行异或运算,得预处理加密图像M(n);
第5步:对M(n)的首行和首列进行添加全“0”标记,得标记图像C(n+1);
第6步:生成随机噪声图像D(r)(r≥2n)和随机整数y,z(0≤y,z≤r-n-1);
第7步:将C(n+1)按照y和z规定的坐标依次替换D(r)中对应的坐标像素,得冗余图像E(r),实现随机嵌入;
第8步:由r和引理1生成一个完备拉丁方W(r)或W(r-1),生成对应的变换矩阵H(r),并将W(r)或W(r-1)定为2级密钥;
第9步:对E(r)按照H(r)的规律进行x次(x≥1)的空间坐标变换,即得最终加密图像F(r),并将x定为3级密钥;
第10步:判断变换任务是否完成,若完成,则直接输出F(r),并终止程序,否则跳转至第9步继续进行.
而其解密操作步骤如下:
第1步:根据2、3级密钥,针对加密图像F(r)进行x次空间坐标逆变换,即得冗余图像E(r);第2步:读取E(r),并判断全“0”标记的坐标位置,然后根据坐标挖取预处理加密图像M(n);第3步:根据1级密钥,将M(n)与A(n)或B(n)按位进行异或运算,得原始图像O(n),并输出O(n).

图1 基于嵌入冗余信息方式的图像加/解密算法流程图
2 算法仿真与参数计算
设计基于以上加/解密算法的程序,在个人PC机上通过仿真软件MATLAB 7.11对一幅256×256的原始灰度Lena图进行多项仿真实验和参数计算.由于预处理阶段中第1级密钥A(n)的构造方法、类型均不固定,因此,以下仿真实验中可采用定义3的方法构造一个A11(256)作为第1级密钥.
2.1 预处理阶段的统计特性仿真与分析
程序对大小为256×256的原始灰度Lena图O(256)进行预处理加密仿真,得其加密前、后的效果图和像素分布直方图,如图2、图3所示.

图2 原始Lena图及其直方图

图3 预处理加密图及其直方图
由图2和图3可得,预处理加密后的图像M(256)比原始图像O(256)的安全性更高,除少部分轮廓信息外,大部分信息都已被很好地隐藏起来了.将两者的直方图进行对比可得,后者的统计特性比前者更好,像素值分布相当均匀.由此说明基于拉丁方的图像预处理加密可降低图中各像素之间的相关性,达到了隐藏图像信息的目的,从而产生抵抗统计分析攻击的作用.
2.2 预处理图像的深度加/解密仿真与分析
先对预处理后的M(256)添加全“0”标记,得到标记图C(257),如图4所示.然后生成一个随机噪声图像D(512),并将C(257)随机地嵌入其中,得到如图5所示的冗余图像E(512).再对此冗余图E(512)进行x=1和x=10次空间坐标变换加密,可得两者的最终加密效果图F(512),如图6所示.

图4 预处理加密图及其标记图

图5 随机噪声图及冗余图

图6 进行1次和10次空间坐标变换后的效果图
基于以上解密算法思路设计解密程序,先对以上加密x=10次后的图像进行10次逆变换解密,得其解密效果,如同7所示.然后根据图中的全“0”标记挖取出预处理图像,并进一步解密,得其解密效果,如图8所示.

图7 进行10次逆变换前、后效果图

图8 挖取图及其解密效果图
从图4~图6可得,将预处理后的加密图嵌入较大的随机噪声图中后经过一定次数的空间坐标变换,使得图像中所有信息都得到了很好的隐藏,在视觉效果上,根本无法识别出原始图像的任何信息.由图7~图8可得,不但能够解密出所需图像,而且还与原始图像吻合得非常好.由此说明该加密方案确实有效,得到的加/解密效果好,并可大幅度地提高图像的安全性.
2.3 密钥空间分析
从前面的算法步骤可以看出,加密密钥由3级密钥构成.由引理2和参考文献[14]可知,第1级密钥的密钥空间随拉丁方阶数n急剧增加,当n=11时,就已超过1050.若阶数再大,则其密钥空间将无法估计.由文献[12]可知,第2级密钥的密钥空间至少为n(n-1)/2,还有可能随着完备拉丁方阶数的增加而增加.第3级密钥x的密钥空间就更大了,因为x的取值范围一般为:x≥10.当对嵌入的图像进行再次加密时,密钥空间主要由第2级密钥和第3级密钥的密钥空间所决定.由于第3级密钥的密钥空间几乎是无限大,因此,由以上3级密钥构成的密钥空间将大到无法计算,若他人想通过枚举方式进行破解加密图像,则是不可能成功的.在解密时,即使有微小的一部分密钥出错,也不能解密出正确的图像,只有使用正确的3级密钥才能解密出正确的图像.若使用不同的原始图像、不同的密钥,则可得到不同的加密效果,说明加密图像对原始图像和密钥充分敏感.
2.4 图像参数计算与抗攻击实验
目前,学界对不同的图像加密算法提出多种评定方法[19-22]. 本文根据各法之优点,主要从不动点比、信息熵、相邻像素的相关性、扩散性与抗差分攻击这样4个方面进行相关的计算和分析.抗攻击实验的分析,则从统计分析攻击、差分攻击、剪切攻击、椒盐噪声攻击、JPEG压缩攻击、Gaussian低通滤波攻击等角度进行仿真及分析.
2.4.1 不动点比
由表1可得,相比于原始图像O(256)而言,预处理图像M(256)的不动点比已经非常低,然而经过冗余信息嵌入后的10次深度变换加密得到的图像F(512)的不动点明显更低.从统计分析角度看,若不动点比越低,则像素变化得越多,图像的像素分布就会更加均匀.

表1 目标图与加密图的不动点比
2.4.2 信息熵
由表2可知,原始图像O(256)经过预处理得到的图像M(256)的信息熵7.997 1已经非常接近理想值8,而嵌入冗余信息后经过10次深度变换得到的加密图F(512)的信息熵7.997 7却更加接近最大值8.此结果可说明该算法能够有效地打乱图像中各像素的分布,提高图像的安全性.

表2 目标图与加密图的信息熵
2.4.3 相邻像素的相关性
对加密图像而言,若图像中各像素相关性越小,则说明加密效果越好,反之效果越差.先从原始图像和最终加密图(x=10次的加密结果)中分别在水平相邻、垂直相邻、对角线相邻这3个方向上随机选取3 000对像素,然后根据式(2)~式(5)计算各像素对的相关性,并得到了数据,具体见表3.加密前、后在水平方向上的相关性比较见图9和图10(以下各式中,x,y均为相邻像素的灰度值).
(2)

(3)

(5)
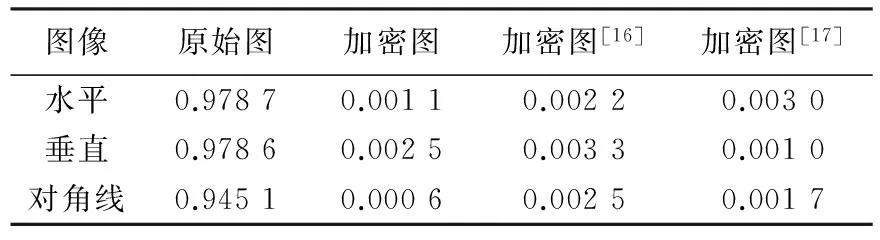
表3 3个不同方向上相邻像素的相关性比较

图9 原始图的水平相关性图示
由表3和图9、图10可得,原始图像无论在哪个方向上各像素的相关性都比较大,并且在0.94以上,而本文的加密图像在水平、垂直、对角线这3个方向上的相关性都比较低,且对角线上都已低到0.000 6.与文献[16-17]中的值对比,更能说明本文算法得到的加密图像中各像素的相关性较低.

图10 加密图的水平相关性图示
综合图2、图3的直方图,表1、表2、表3中数据,以及对图9、图10等的分析可得,本文提出的加密方案确实有效地抵抗了统计分析攻击.
2.4.4 扩散性与抗差分攻击
在扩散性分析中有2个重要参数:像素改变率(number of pixels change rate,NPCR)和一致平均改变强度(unified average changing intensity,UACI)[23],常被用来作为评价图像加密算法抗差分攻击的主要指标.
设有2幅加密图像X1和X2,两者加密前的原始图像只有1个像素不同,且两者在相同坐标处的像素为X1(i,j)和X2(i,j),则有:
(6)

(7)
(8)
选2幅仅相差一个像素的256×256阶Lena图,经过相同加密算法、相同密钥加密得到了2幅完全不同的加密效果图.由式(6)~式(8)计算在不同加密次数时的NPCR和UACI值,如图11、图12所示.

图11 不同加密次数时的NPCR值
由图11、图12可得,虽然加密次数x不同,但NPCR和UACI值均相对稳定,并且NPCR值保持在99.60%~99.61%.已知256级灰度图其理想NPCR=99.609 4%,而本文得到的NPCR值与之符合得很好,说明该加密算法对明文(原始图像)非常敏感.即使2幅原始图像仅相差一个像素,但加密后的图像却完全不同,说明该加密方案的扩散性非常好,扩散速度很快,具有很强的抵抗差分攻击能力.

图12 不同加密次数时的UACI值
2.4.5 抗攻击仿真及其结果分析

图13 抗1/16剪切攻击及解密恢复图

图14 抗1/4剪切攻击及解密恢复图

图15 抗1/2剪切攻击及解密恢复图

图16 抗3/4剪切攻击及解密恢复图

图18 抗JPEG压缩攻击及解密恢复图

图19 抗Gaussian低通滤波攻击及解密恢复图
图13~图19均是采用256阶Lena图进行x=10次坐标深度变换加密后,再进行抗剪切攻击、抗椒盐噪声攻击、抗JPEG压缩攻击和抗Gaussian低通滤波攻击的仿真实验.从以上受到不同攻击后得到的解密效果图看,虽然解密图像没有原始图像那样完整,但是仍然保留了很多原始图像信息.由此可得,如果通信过程中密钥保管安全,那么本文的图像加密算法能较好地抵抗外界的攻击.
从抗剪切攻击仿真实验可得,当加密图像受到剪切攻击时,部分图像信息虽然会丢失,但仍可较大程度地恢复出原图像的基本信息.图像受到剪切攻击还能够恢复的原因,是因为坐标深度变换加密可使原图中所有信息都比较均匀地隐藏在一幅较大的噪声图像中,在剪切时就不至于丢失所有信息,在解密时只要在剪切图像中能找出原来存留的部分原图信息(比如“全0”标记),就可最大限度地进行恢复.若被剪切的信息量占总信息量的比例太大,则不能有效地恢复出原图. 只要被剪切的信息量不太大,就不必担心找不到“全0”标记,因为“全0”标记也会被均匀地分散到噪声图像中,在剪切时总会存留一部分.
由此可得,该图像加密算法可对外公开,只需保管好加密密钥,通过安全的专用信道进行传输密钥,就可保证图像通信的安全性,并能较好地抵抗外界攻击.
3 结 论
网络通信不但需要良好的网络环境,而且还需要更高的通信技术保障.在网络通信中,有很多关键性技术问题倍受关注,而图像通信的安全性问题更是重点.设计性能优良的图像加密算法可以有效地增强图像的安全性、提高图像通信的质量.本文在研究完备拉丁方的扩展性质后,提出了基于嵌入冗余信息方式的图像加密方案,并设计了相应的加/解密算法步骤,进行了一定量的相关仿真实验和参数计算.从加密算法步骤和流程图角度看,该算法简单、计算量少、易于实现.从加/解密效果看,其效果都非常理想,不少性能都接近理论最好值.从参数计算和抗攻击仿真实验结果看,该加密算法可抵抗多种外界攻击,比如统计分析攻击、差分攻击、剪切攻击、压缩攻击、滤波分析等.从以上角度可以说明,该图像加密方案比文献[10-13]中的方案适用性更强.由于拉丁方的计算模式多、类型多、数量庞大、密钥空间非常大,所以基于拉丁方的图像加密方案有很大的安全性.本文所提图像加密方案比基于光学方法的图像加密方案更加简单、硬件要求低.和基于混沌系统或者超混沌系统的加密方案相比,总体效果相当,在相邻像素相关性指标上要略好,而且方案简单,密钥空间更大.和传统的基于拉丁方的方案相比,则具有很强的抗差分攻击能力,一些性能指标几乎达到理论极限,其他各项指标也更加好.因此,本文所设计的图像加密方案具有较大的实用价值.
[1]Hui Y Q,Dong Z,Ji Y Z.Human visual system based adaptive digital image watermarking[J].Signal Processing,2007,88(1):174-188.
[2]徐光宪,李玉华,张鑫.基于幻方变换的抗剪切扩频水印算法研究[J].清华大学学报:自然科学版,2013,53(8):1087-1090.
[3]Chen C H,Tang Y L,Wang C P,et al.A robust watermarking algorithm based on salient image features[J].Optik International Journal for Light and Electron Optics,2014,125(3):1134-1140.
[4]王金伟,周春飞,王水平,等.基于分数阶四元数傅里叶变换的彩色图像自适应水印算法[J].电子与信息学报,2016,38(11):2832-2839.
[5]项世军,罗欣荣,石书协.一种同态加密域图像可逆水印算法[J].计算机学报,2016,39(3):571-581.
[6]汤永利,高玉龙,于金霞,等.基于DCT域的增益不变量化的数字图像水印算法[J].重庆邮电大学学报:自然科学版,2017,29(2):223-231.
[7]Lu D,Jin W M.Fully phase color image encryption based on joint fractional Fourier transform correlator and phase retrieval algorithm[J].Chinese Optics Letters,2011,9(2):34-36.
[8]Cai J J,Shen X J,Lin C.Images encryption based on joint transform correlator and vector decomposition[J].Journal of Optoelectronics Laser,2015,26(5):1005-1009.
[9]曾大奎,马利红,刘健,等.基于两步正交相移干涉的振幅图像光学加密技术[J].光子学报,2012,41(1):72-76.
[10]李国富.基于正交拉丁方的数字图像置乱方法[J].北方工业大学学报,2001,13(1):14-16.
[11]巨亚荣,刘小兵.一种基于Logistic模型和正交拉丁方变换的图像加密方法[J].重庆科技学院学报:自然科学版,2008,8(10):143-146.
[12]杨刘洋,吕翔.一种基于完备拉丁方的图像加密算法[J].计算机应用研究,2015,32(11):3433-3442.
[13]吕翔,杨刘洋,刘中帅.一种无损伤的图像加密算法与实现[J].浙江师范大学学报:自然科学版,2017,40(2):153-160.
[14]杨刘洋.拉丁方在二维光正交码和图像加密中的应用研究[D].金华:浙江师范大学,2015.
[15]Wang X Y,Teng L,Qin X.A novel colour image encryption algorithm based on chaos[J].Signal Processing,2011,92(4):1101-1108.
[16]廖雪峰,邹华胜.超混沌图像加密方案的分析与改进[J].计算机工程与应用,2012,48(33):105-111.
[17]陈在平,蔡鹏飞,董恩增.基于超混沌AES图像加密算法[J].吉林大学学报:信息科学版,2013,31(2):158-164.
[18]胡春杰,陈晓,郭银.基于多混沌映射的光学图像加密算法[J].激光杂志,2017,38(1):110-114.
[19]徐江峰,杨有.加密图像置乱性能分析[J].计算机科学,2006,3(33):110-113.
[20]王迤冉,王春霞,詹新生.一种图像加密算法的性能评价方法[J].微计算机信息,2006,22(10-3):313-314.
[21]黄建,柏森.一种有效的图像置乱程度衡量方法[J].计算机工程与应用,2009,45(30):200-203.
[22]卢振泰,黎罗罗.一种新的衡量图像置乱程度的方法[J].中山大学学报:自然科学版,2005,44(6):126-129.
[23]张同峰.基于一维复合混沌映射的数字图像加密算法研究[D].兰州:兰州大学,2016.
