品味类比，直觉与发敖

常文武+文江

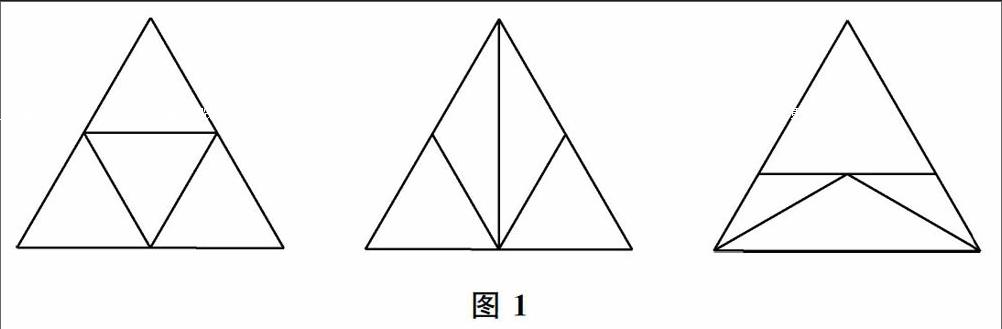
人与人相遇是缘，人与题目相遇也是缘.偶有学生来问：如何找m三种方法将正三角形切割为4个等腰三角形？

师生讨论出的答案如下：

前两种方法一目了然（但解讀有多种）.第三种却不易一眼发现水平线的具体位置.需申明水平切割线是过几何对称中心（重点）.

作为求教者，学生已经释然.作为老师却感觉有必要继续引申一番，于是追问：如果题目改为“找出将一个等腰三角形切割为4个等腰三角形的方法”，又将如何求解呢？

请读者类比一下：以上关于等边三角形的结果是否可以行得通呢？

第一种“联结中点”法得到的是与初始等腰三角形相似的四个全等三角形，所以形状保持了大三角形等腰的形状；对第二种切法，利用直角三角形斜边中线长等于斜边一半的性质可轻易判定.（不过这只是一种解读和推广，读者读到文末白会领会）

第三种方法就不敢保证了，

调动直觉思维，如果等腰三角形比较“瘦”，似乎只要让方法三的水平切割线下移一些就可以满足要求.而对于“胖”的等腰三角形，应该上移那条水平切割线.总之，方法应该可行！

那么如何找到切割位置呢？自然想到设未知数来解方程.

对于图2的等腰三角形，设BD长为未知数x.AB=AC=a，BC=b为已知数.根据题设，DE= 2x，DE∥BC.利用相似，可得AD：AB=DE：BC，即a-x：a=2a：b.解得x=ab/（2a+b）.

既然第三套切法也有了推广的解，问题似乎得到了“圆满”解决：任何等腰三角形同样能如同等边三角形那样有三种方法切割为4个等腰三角形.

一个更大胆的问题冒出来了：这是全部的解吗？

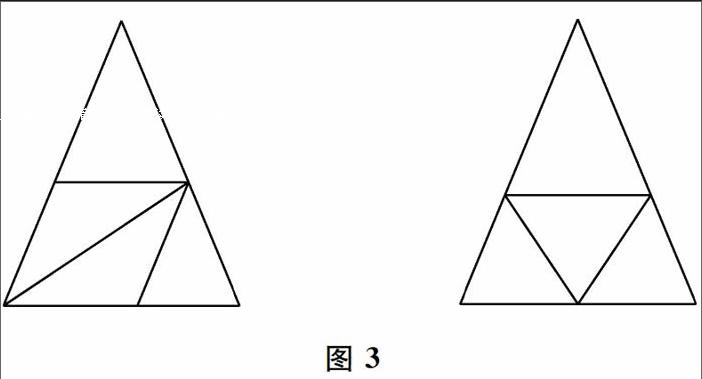
本文第二作者利用对前面两个切法的不同解读，竟然义拓展产生了两个“衍生产品”.请看图3（不要忽略钝角三角形也必须满足条件）.

从图3中可以看出，有一个切法是边中点联三角形的推广，打破了只有联结中点才行的“神话”.另外一个方法是“个”字型切割法，它是原先方法二的再推广.改变了“个”字起笔（即为角平分线）在底边的套路.

这样，针对新的问题“切等腰三角形为4个等腰三角形”一共找到了五种方法：倒三角切法二种，“个”字切法二种和K字切法一种.

你还能找到其他解法吗？

看来哪怕是课本配套习题册上面的普通题目，只要勤思考多动脑去发散思维，有趣又深刻的结果就有可能被你发现.如果再把心得及时记录下来写成文字，你必定会在数学甚至语文学科上都取得骄人的成绩.endprint