巧用类比学概念、性质
2018-03-06周春元
周春元

类比思想是同学们在数学学习过程中常用的一种重要的思想方法,它是指同学们在学习过程中将新事物与旧事物之间的某些方面作类似的比较,把已经获得的知识、方法、理论迁移到新事物中,从而解决新问题.其思维过程大致如图1所示:
观察、比较→测新的结论→联想、类推
同学们在学习有关数学概念、性质等的时候,如果能够学会用类比思想来学习理解、消化记忆,将会大大降低学习数学的难度,提高学习数学的兴趣,从而让同学们不再害怕数学,使数学成为同学们的好朋友.在数学学习的过程中,很多方面同学们都可以利用类比思想来学习,下面举几个必修中的例子.
一、立体几何学习中的类比
立体几何初步这一章的学习使同学们从初中熟知的平面几何一下子跃人高中陌生的空间立体几何.很多人不能够适应这种变化,感到立体几何的学习比较困难、抽象.因此,在学习过程中,同学们要学会培养自己的类比推理的思维,掌握二维与三维之间某些方面的相通或相似点.
案例1 球的概念及性质类比
圆与球在它们的生成、形状、定义等方面都具有相似的属性.据此,在网与球的相关元素之间建立如图2所示的对应关系:
根據圆的性质,可以类比球的性质如表1:
案例2 四棱台概念的类比
梯形与四棱台在它们的生成、形状、定义等方面都具有相似的属性.据此,在梯形与四棱台的相关元素之间建立如表2的对应关系:
从而,梯形可以认为是用平行于三角形一边的直线截去一个小三角形后得到的,而棱台则可认为是用平行于棱锥底面的平面截去一个小棱锥后得到的.故有如图3所示的对应关系:
进而可得到图4所示的对应关系:
立体几何学习中的类比,实际上是把平面几何从二维推广到三维,只要注重它们之间的联系、类比,立体几何一定难不倒我们.
二、平面向量学习中的类比
由于平面向量是新生事物,同学们对其中共线向量、平面向量的理解存在困难,特别是对共线向量定理、平面向量基本定理之间的关系在思维上容易产生混淆,因此,同学们在学习过程中,可以将共线向量与平面向量进行类比学习.
案例3平面向量定理的类比
平面向量定理学习的类比实际上只是把一维向量推广到二维向量.通过这种类比方法在以后的空间向量的学习过程中,我们也可以类比得出空间向量基本定理.也就是说,向量的类比学习可如图5所示:
一、数列学习中的类比
数列这一章的学习过程中,同学们在学完等差数列之后学习等比数列时,就可以利用类比的方法来进行学习.这样,能够对等比数列的学习起到很大的帮助.
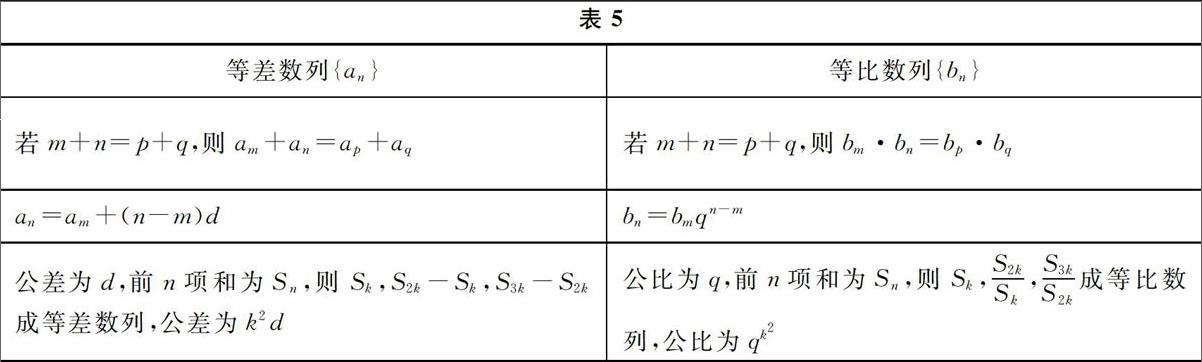
案例4数列概念类比
案例5 数列性质类比
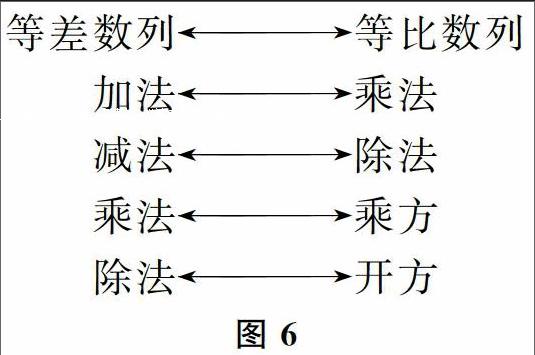
在学习等差数列类比等比数列时,同学们通过上面几个案例可以看出类比的规律,那就是:“等差数列类比等比数列,其运算抬高一级.”
一级运算:加减运算;二级运算:乘除运算;三级运算:乘方开方运算.
类比思想是同学们在接受新生事物时所采用的比较行之有效的方法之一.在学习高中数学的过程中,把新知与旧知中有关联的事物建立内在联系,巧用类比思维帮助自己学习数学的有关知识,将会起到事半功倍的效果.endprint
