理清变化机理 参数刻画运动

漆光宗

运动、变化是绝对的，而静止、不变是相对的，对许多解析几何中的变化型问题，如果能认真地分析运动变化的机理及相互制约的因素，看看是谁引起了运动和变化，就将其作为参数引入，这个参数往往可以作为桥梁，沟通着主要变量之间的联系，明确变量之间的函数关系.参数的变化引起运动，运动就可以由参数来刻画.这样就可以把变化中的量转化为参数的变化，从而使问题的解决变得豁然开朗.

经过定点M（x₀，y₀）的直线l的点斜式方程为：y-y=k（x-x₀），若把斜率k看成参数，则不同的k值对应着经过点M的不同的直线，因此方程就可以表示jL经过点M的除去直线x=x₀。（斜率不存在）的所有的直线.从运动的角度看，k的变化引起了直线l的转动.特别地：方程y=kx+b（k为参数，b为常数）则表示经过定点（O，6）的除去直线x=0的所有直线.

例1 当直线l经过点P（3，2）且与x，y轴正半轴交于A，B两点，点0是坐标原点，当△OAB面积最小时求直线Z的方程.

分析 经过点P（3，2）的直线有无数多条，由于斜率k的变化引起了直线的转动，从而引起△OAB面积的变化，因此可以引入参数k，△OAB面积就可以表示成关于k的函数f（k），这样问题就转化为探求函数f（x）取得最小值时k的取值，从而写出所求直线l的方程.

例2 求与直线3x+4y+l=0平行且过点（1，2）的直线l的方程.

解 设与3x+4V+l=0平行的直线l方程为3x+4y+A—O，

点（1，2）在直线上，则3×1+4×2+λ一0，所以λ=-11，

故所求直线方程为3x+4y-ll=0.

从运动、变化的角度看，曲线可以看成由点的运动所形成，当生成曲线的动点P（称为被动点）随着另一动点Q（称为主动点）的运动而有规律地运动，且Q又落在一给定的曲线C上时，可以把点Q看成参数（称为点参数），只需根据条件去寻找表示P，Q两点间规律的表达式，然后将Q点的两个坐标分别用P点的坐标来表示，再把Q点的坐标代入曲线C的方程.从而得到被动点P的坐标之间的关系，即所求曲线的方程.

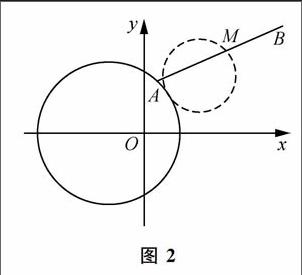
例3 （人教版必修二P129例5）已知線段AB的端点B的坐标是（4，3），端点A在圆（x+1）²+y²=4上运动，求线段AB的中点M的轨迹方程.

分析 如图2，点M为什么运动？是因为点A的运动引起的，因此可以把点A看成主动点（参数），点M看成被动点，要探求被动点M的轨迹方程即探求点M的坐标（x，y）所满足的关系式.而主动点A在已知圆上运动，点A的坐标满足方程（x+1）²+y²=4.建立点M与点A坐标之间的关系，就可以建立点M的坐标满足的条件，从而求出点M的轨迹方程.

解 设点M的坐标是（x，y），点A的坐标是（x₀，y₀）.由于点B的坐标是（4，3），且M是线段AB的中点，所以x=（x₀+4）/2，y=（y₀+3）/2

于是有x₀=2x-4，y₀=2y-3，

①

因为点A在圆（x+1）²+y²=4上运动，所以点A的坐标满足方程（x+1）²+y²=4即（x₀+l）²+y₀²=4，

②

把①代入②，可得（2x-4+1）²+（2y-3）²=4，即（x-3/2）²+（y-3/2）²=1.

所以，点M的轨迹是以（3/2，3/2）为圆心，半径长是1的圆，

参数是刻画运动的好帮手——相信你通过上述的几个例子已经深有体会，通过参数来刻画运动，不但可以揭示运动的本质属性，还能提高我们分析和解决几何问题的能力.endprint