“解几”入门 方法先行

余建国

解析几何（简称“解几”）的本质就是用代数的方法研究几何问题.这里有两个问题：一是研究什么几何问题，二是何为代数方法.“解析几何初步”中对直线与网的研究历程清楚地说明了这两个问题，并且为我们今后学习圆锥曲线奠定了基础.下面以圆为例，与同学们谈谈如何通过研究解析几何的常见问题，把握解析几何学习的典型方法，跨入解析几何的大门.

一、问题与方法

“解析几何初步”中，我们研究了直线和圆，这是平面中两个最基本的图形.正如前面研究直线——建立平面直角坐标系求直线的方程，利用直线的方程研究直线的几何性质一样，对于网的研究，我们同样经历这两个步骤.本期将重点研究圆的几何性质.

1.直线与圆的位置关系

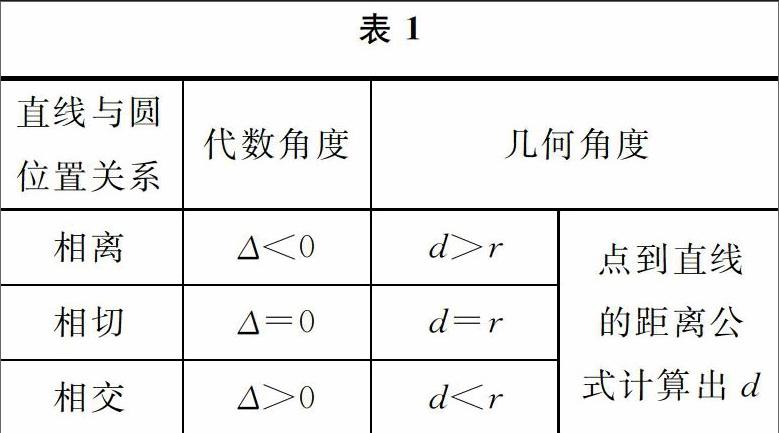
根据平面几何知识，直线与网有相交、相切和相离三种位置关系，并且用同心到直线的距离（d）与圆的半径（r）比较可得，而通过同心坐标与直线方程计算这个距离就是解析几何的“拿手好戏”了；我们还可以从解方程组（直线方程与网的方程联立）——纯粹的代数的角度，考察所得方程组的解的情况判别直线与网的关系.这两种方法都体现了解析几何在沟通代数与几何上的桥梁作用.具体结论见表1.

2.相交时的弦长问题

当直线l与网C相交时，连结两个交点A，B的线段AB称为圆的弦，

从代数的角度看，只要通过解方程组求得两个交点A，B的坐标（x₁，y₁），（x₂，y₂），利用两点间的距离公式：求得距离，如果直线AB的斜率k存在的话，也可以写成：

3.相切时的切线问题

直线与网相切，常见的问题是求切线方程，求切线长、范围和最值等.

从代数的角度看，直线与网相切时，△一0，这是一个方程，一般通过这个方程就能求解一个未知数，例如切线的斜率（如果直线的斜率存在）；而从几何的角度看，直线与网相切时，d=r，同样这个方程也能求解切线的斜率.特别地，在已知切点的情况下，利用切点与网心的连线与切线互相垂直，可以直接确定切线的斜率，课本上习题提供了这个问题的结论：

4.圆与圆的位置关系

将两个圆的方程联立，解所得方程组.若方程组没有实数解，说明两个网没有交点（公共点），此时两圆是相离，还是内含就需要结合图形来看，因此，纯粹的解方程组手段就没有表2的判断方法简洁，表中d是两圆心0₁，Q₂间的距离，R，r分别是两圆半径（R≥r）.

二、示例与思想

在求解网的问题时，一方面，通过分析图形，找出可以使用的几何关系，并尽可能地将几何语言转化为代数语言，用坐标、方程等代数语言去表征、去求解；另一方面，由于在初中的平面几何学习中，较多地了解了网的有关性质，因此充分利用网的已有的几何性质，例如垂径定理，实现代数运算的简化，也是同学们需要感悟的解题思想.

例 已知圆C：x²+y²+x-6y+m=0与直线l：x+2y-3=0相交于A，B两点，若以AB为直径的圆通过坐标原点O，求实数m的值.

分析一 “以AB为直径的网通过坐标原点0"，一方面，转化为代数语言就是原点0（0，0）的坐标满足以AB为直径的圆的方程，若设交点A（x₁，y₁），B（x₂，y₂），则以AB为直径的圆的方程是（x-x₁）（x-x₂）+（y-y₁）（y-y₂）=0，原点O在网上等价于（O-x₁）（0-x₂）+（0-y₁）（O-y₂） =O，即XlX2+y.Y2 =0；另一方面，这句话也等价于OA上OB，当X₁=O（y=0）或x₂=0（y₁=0）时，满足x₁x₂+y₁y₂=O，当x₁·x₂≠0时有k_OA=y₁/x₁，k_OB=y₂/x₂，由k_OA1·k_OB=-1得x₁x₂+y₁y₂=0，因此对所有A，B都满足x₁x₂+y₁y₂=0，殊途同归，

分析二 从代数的角度想，求解一个未知数出，只需找到一個含m的方程，“算两次”是典型的建立方程的方法.在图1中，取线段AB中点M，由于CM⊥AB，可以求得直线CM的方程，从而得到M的坐标，于是OM长可求，由于OA⊥OB，而M是线段AB的中点，所以OM=1/2AB—AM，另一方面，可以通过类似于求弦长的方法求得AM，于是建立方程OM=AM求得m

略解二 取线段AB中点M，由CM-LAB可得直线CM的方程为2x-y+4=0，与AB方程联立，得M（-1，2），所以Am₂=OM₂=5.

另一方面，因为cM₂=5/4，CA₂=r₂=37-4m，在Rt△ACM中，有AM2一r2CM₂=8-m.所以8-m=5，解得M=3.

反思 将几何语言转译为代数语言，并通过代数（坐标、方程）运算解决几何问题是解析几何的本质方法.而研究直线与网的位置关系时，涉及的二元二次方程组的处理方法也是将来进一步研究圆锥曲线的通法.需要指出的是，由于我们在初中学习过网的几何性质，如垂径定理，因此解决直线与圆的位置时，也要尽可能地挖掘其平面几何性质，这样，需要转化为代数语言的部分越少，计算的量和障碍就越少，真正发挥数形结合的优势.

总之，同学们在学习直线与圆的几何性质的过程中，不仅要学会相应的数学知识，更重要的是领悟解析几何的思想方法，发挥坐标法研究问题的统一性、程序性和简洁性，善于将几何语言转化为代数语言，从不同的角度表征数学问题，从而寻求问题的解.

巩固练习

1.过点（3，1）作圆（x-1）²+y²=1的两条切线，切点分别为A，B，则直线AB的方程为

（

）

A. 2x+y-3=0

B.2x-y-3=0

C.4x-y-3=0

D.4x+y-3=0

2.过点（3，1）作网（x-2）²+（y-2）²=4的弦，其中最短的弦长为_______.endprint