一种基于MRⅡ算法的三层二值双向联想记忆网络

徐 彦,熊迎军

(南京农业大学信息科学技术学院，江苏 南京 210095)

1 引言

联想记忆是神经网络一个重要的应用，多种神经网络如Hopfield网络、Cellular网络、混沌神经网络以及双向联想记忆BAM(Bidirectional Associative Memory)网络等都可以用来实现联想记忆功能。双向联想记忆网络最初是由Kosko[1]提出的，是一种双向运行的采用全连接两层结构的网络，可以用来存储、记忆两组对应的模式。自从BAM网络被提出之后，很多研究者提出了很多不同的双向联想记忆网络结构或算法[2]，到现在依然不断有最新的研究成果发表[3]。在文献[1]中，作者采用Hebbian规则训练网络权值存储模式对，Hebbian学习规则的主要缺点是对非正交的模式对学习能力很差。

文献[4]提出了BL(Bidirectional Learning)算法训练BAM网络。这个算法使用感知机规则训练网络的权值。文献[5]提出了PRLAB(Pseudo-Relaxation Learning Algorithm for BAM)算法，该算法通过迭代的方法，依次将模式对输入网络学习调整权值，迭代的初始权值是随机选取的。文献[6]将Hebbian规则和PRLAB算法结合起来提出了QLBAM(Quick Learning for BAM)算法。该算法的迭代步骤和PRLAB一样，所不同的是将用Hebbian规则得到的权值矩阵作为迭代的初始权值，因此其存储模式的能力不低于PRLAB算法，但是收敛的速度更快。

两层BAM网络的存储能力是由两层神经元的个数，或者说是由需要存储的模式对的维数决定的，若模式对过多，网络会无能为力。另外，以上介绍的学习算法只有当模式之间是正交时训练的效果才会比较好。以上两点限制了BAM网络的存储能力。一个有效提高BAM网络存储能力的方法是扩大网络的结构，构建三层或多层BAM网络。但是，网络层数的增加会导致学习难度的增加。一个可行的方法是采用具有连续型激活函数的神经元，然后用类似BP的算法实现三层网络的学习[7]。

最初的BAM网络是一个二值网络，即存储模式的元素只有两个值(-1或1)。输入输出只处理二值的神经元以硬极限函数作为激活函数，其结构简单、运行效率较高。很多实际问题处理过程中只涉及两个值，解决这类问题时，若采用连续型网络，会引起输出结果二值化的误差和效率的降低，采用二值网络处理有着固有的优势。因此，二值神经网络依然具有较高的研究价值。目前，具有三层结构的二值BAM网络的研究还很少。

三层二值BAM网络的难点在于学习。因为神经元采用硬极限函数，所以其无法利用梯度下降以及误差反向传播实现三层网络权值的调整。利用前馈神经网络的学习算法实现BAM网络的学习是被研究者多次采用的方法。与三层二值 BAM网络对应的前馈神经网络是多层二值前馈网络，这被研究者称为Madaline网络[8]。该网络目前最成功的学习算法称为MR II(Madaline Rule Ⅱ)算法[9,10]。实验表明MR Ⅱ算法具有较强的性能。

为了克服两层BAM网络的缺点，同时避免采用连续型网络处理二值模式所带来的问题，本文提出一种三层结构的二值BAM网络TLBBAM(Three-Layer Binary BAM)。通过在传统的两层BAM网络之间加入一个中间层，极大地提高了网络的存储容量，同时也提高了网络存储小差别与非正交模式的能力。TLBBAM中神经元的激活函数为硬极限函数，采用 MR Ⅱ算法训练网络权值存储模式对，使得网络的输入、输出、运行及权值的训练等全部采用二值处理。目前，研究者对BAM网络的研究更多的集中在复杂的连续型BAM网络的稳定性理论上[11,12]，TLBBAM作为一种新的BAM网络结构与学习算法可以从另一个重要方面拓展与完善BAM网络的研究，因此具有较高的理论与实际意义。

2 TLBBAM的结构以及学习算法

2.1 两层BAM的结构及QLBAM算法

三层二值BAM网络以两层二值BAM网络为基础。如图1所示，初始的两层BAM网络由X层和Y层构成。

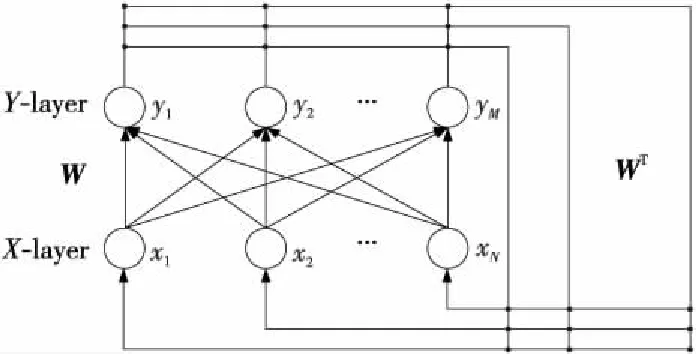
Figure 1 Two-layer BAM network图1 两层BAM网络

(1)

(2)

其中,λ,ξ为参数。当Y(k)输入到Y层，若在X层模式输出错误，也需要调整权值和偏置值，其调整规则与式(1)和式(2)完全类似。

2.2 TLBBAM的结构

本文提出的TLBBAM网络为三层结构，即在传统两层BAM网络的X层和Y层之间加上一个中间层。其结构如图2所示。其中X层和Y层的功能与两层BAM网络一样，负责模式的输入与输出，H层为中间层。

Figure 2 Three-layer Binary BAM图2 三层二值双向联想记忆网络结构

其中，(W1)N×T为X层和中间层之间的权值矩阵，(W2)T×M为中间层和Y层之间的权值矩阵，θx和θy分别为X层和Y层的偏置，θh为中间层的偏置，N、M、T分别为X层、Y层和中间层的神经元个数，k∈{1,…,K},K为存储的模式对个数。网络X层和Y层神经元的个数由所存储的模式对的维数决定，中间层神经元的个数是一个可以调节的参数，理论上中间层神经元个数越多，网络的存储能力越强，可以存储的模式对越多。

2.3 TLBBAM的学习算法

TLBBAM网络的学习算法，我们引入二值多层前向网络Madaline的MR Ⅱ算法[8]。MR Ⅱ算法是一种有监督的学习算法，网络的训练过程实际上就是对网络的权值与偏置值调节的过程。对权值和偏置值的每一次调节，总希望在满足当前样本学习的同时，尽量使得本次学习对网络总体的结构改变最小，这样就可以让网络通过前面样本学习到的性能得到最大限度的保持。这就是MR Ⅱ算法的理论基础“最小扰动原则”。

假设有一个三层Madaline网络。网络在学习过程中，权值的调整从中间层到输出层依次进行，一次完整的学习过程称为一次迭代或一个学习周期。设当前为第k次迭代，按照最小扰动原则选择网络某一层的一个神经元翻转其输出状态作为期望输出计算调整该神经元的权值。此时，以神经元的“信任度”，即该神经元内部此次运行的加权和的绝对值|u|=|W(k)X(k)|作为衡量该神经元权值改变对整个网络影响程度的指标量，其中W(k)和X(k)分别为神经元的权值和输入向量。并且规定，当某个神经元的信任度大于某一数值δ时，不对这个神经元的权值进行调整，对于其它的神经元按照信任度从小到大依次选择进行学习。权值调整后若网络的最终实际输出更接近网络的最终期望输出，则保留这次翻转。具体的权值调整公式为:

W(k+1)=

其中，n为当前神经元的输入维数，η为确保输出翻转的常数，d(k)为神经元的期望输出，L是一个常数。该算法重复上述的过程，直到网络训练成功或者达到某一最大训练迭代次数为止。

TLBBAM借助于MR Ⅱ算法可以成功地将X层、中间层和Y层连接起来实现模式对的训练存储。在学习过程中，依次使用需要存储的K个模式对V={(X(k),Y(k))},k=1,…,K训练网络。对于每一对模式(X(k),Y(k))，在网络的两个方向上都训练一次。首先从X层到Y层，将X(k)看成Madaline网络的输入，Y(k)看成Madaline网络的期望输出，利用MR Ⅱ算法，训练网络的权值和偏置值。接着从Y层到X层，将Y(k)看成Madaline网络的输入，X(k)看成Madaline网络的期望输出，利用MR Ⅱ算法，训练网络的权值和偏置值。这样循环下去，直到网络成功收敛或者达到某一最大循环迭代次数。本文中学习收敛指的是通过训练网络可以成功地存储并正确回忆所有待存储模式对。

TLBBAM的学习算法可以表述为：

(1)在训练的初始阶段，随机选择一组数作为网络的初始权值和偏置W1,W2,θx,θy,θh。

(2)重复运行下列学习周期，直到收敛或达到某一个最大学习周期数：

对需要存储的模式对V={(X(k),Y(k))},k=1,…,K，作如下循环，Fork=1 toK

①将X(k)作为输入，Y(k)作为期望输出，利用MR Ⅱ算法，在X层到Y层方向上训练网络;

②将Y(k)作为输入，X(k)作为期望输出，利用MR Ⅱ算法，在Y层到X层方向上训练网络;

Nextk

(3)测试以上学习得到的网络权值和偏置值。

3 实验

下面我们用几组实验来验证TLBBAM网络存储模式的能力。在第一组实验中我们存储0～9这10个数字的点阵模式与它们的二进制模式组成的模式对。数字的点阵模式用二值10×8方格表示，黑的方格为-1，白的方格为1。标准的二进制是由0，1表示的数字，在这里我们将0用-1代替。因为10个数字的二进制模式只需要四位二进制数，所以我们用二值1×4方格表示。如图3所示，上面的10个是数字的点阵模式，下面的10个是二进制模式，两两对应组成10个模式对。

Figure 3 Lattice and binary models of numbers图3 数字的点阵模式和二进制模式

二值1×4方格总共有16个，其中数字模式占去10个，还剩下6个。为了增加学习的难度，在这6个中我们选出4个，和加、减、乘、除这四个运算符的点阵模式组成模式对，并且将剩下的2个和另外2个随机产生的10×8点阵模式组成模式对，如图4所示。这样，需要存储的模式一共有16对。这里用X(k),k=1,…,16来表示数字和运算符的点阵模式，用Y(k),k=1,…,16来表示数字的二进制以及运算符的四位模式，上标中1～10依次为数字1～9和0，11～14依次代表加、减、乘、除四个运算符，15、16代表随机模式。

Figure 4 Lattice and four bit binary models of operators and random models图4 运算符及随机模式的点阵模式和四位模式

这个例子有如下几个特点。第一，实验中的四位模式使用了全部的16个四位二值向量，我们称之为模式的饱和存储问题，模式中有的模式之间差别很小，比如数4和5的二进制只相差末尾的1位，在学习结束回忆模式时任何误差都会导致回忆出的是另一个模式，这需要网络提供足够强的模式区分能力；第二，模式对之间不是两两正交的;第三，一个模式对中80维向量对应于4维向量，向量维数之间差距很大。这些都增加了学习存储模式的难度。

首先我们采用传统两层二值BAM网络来学习存储这16对模式，网络的X层有10×8=80个神经元，Y层有4个神经元。实验中我们采用RPLAB和QLBAM算法训练网络，每次实验迭代周期的最大值设置为1 000次。实验结果表明,两层结构的BAM网络在任何实验设定下都无法将这16对模式全部存储进网络。以性能最强的QLBAM算法为例，图5显示了经过训练之后将两组模式中的前14个分别从两个方向输入网络后得到的对应模式回忆结果。由图5可知，网络经过训练后模式联想回忆的结果很差，点阵模式除了一个能完美回忆，4个回忆有噪音以外都没有正确回忆出来，而四位模式只有5个能正确回忆。这说明两层BAM网络整体存储这16对模式的性能很差。

Figure 5 Recall results of TLBBAM for 16 pair models图5 两层二值BAM网络回忆16对模式的结果

在实验中如果只选择16对模式中的一部分进行学习，则存储性能会有所提高。例如，如果只学习7～14这8个模式对，两层二值BAM网络采用QLBAM算法可以训练成功。这也是两层BAM网络学习这16对模式存储结果最好的情况，或者说对于这个例子两层BAM的存储性能在此时达到极限。

接下来我们采用本文提出的TLBBAM网络来学习存储这16对模式。实验中X层和Y层的神经元个数和上面的两层BAM网络一样，中间层神经元的个数设置为从10个开始，每次增加两个，逐渐增加到34个。实验中MR Ⅱ算法参数选择如下:δ=6.5,η=0.4,L=3.5；网络的初始权值和偏置值随机选择由1或-1组成的矩阵和向量。每种情形下进行100次实验，每次实验的最大迭代周期数设置为500，记录网络能成功存储并回忆所有16对模式的实验次数以及这些成功实验中网络学习所需要的平均周期数。实验的结果如表1所示。

Figure 6 An experimental result of TLBBAM learning 16 pair models图6 TLBBAM学习存储16对模式的一次实验结果

神经元个数成功次数学习周期神经元个数成功次数学习周期107136249988123310226998014609928100821673953010078189392321007820978734100732299 88

从表1可以看到，随着中间层神经元个数的逐渐增加，学习成功的次数也随之增加。在中间层只有10个神经元时，只有大约7%的实验可以成功存储这16对模式；当中间层神经元个数超过26个，每一次实验都可以成功地将16对模式存储进网络，即此时成功率为100%。因此，两层二值BAM无法成功存储16个模式对，采用TLBBAM网络可以成功存储并正确回忆。实验的结果说明，TLBBAM网络相比较两层BAM网络在模式记忆与区分能力上有了极大的提高，可以有效解决饱和模式存储问题。观察表1中的学习周期可知，随着中间层神经元个数的增加，学习周期数呈现逐渐下降的趋势，这说明增加中间层神经元个数可以提高网络的学习效率。

图6显示了当中间层神经元个数为10时某一次没有成功的实验在训练结束后前14个模式对的回忆结果。此时，数字与运算符的点阵模式有2个回忆错误，有1个回忆时出现噪音，其余全部正确；而四位模式中只有2个回忆错误，总体错误率较低。对比图5可知，虽然在这次实验中训练没有收敛，但是模式回忆的结果也明显好于两层BAM网络。

下面考察TLBBAM网络的存储容量，训练网络存储6×5的随机模式对。图7显示了五对随机产生的6×5模式。实验先采用两层BAM网络结合QLBAM算法，网络的X层和Y层各有30个神经元，QLBAM的两个训练参数设置为λ=1.5,ξ=0.05。实验中存储的模式对个数从30个开始逐步增加，每种情况进行50次实验，每次实验学习的最大迭代周期数设置为1 000。实验结果显示，QLBAM算法可以使两层BAM网络最多成功存储39对随机模式，此时训练成功平均需要115个迭代周期。

Figure 7 Five pairs 6×5 models generated randomly图7 随机生成的5对6×5模式

接着，我们采用TLBBAM网络来存储6×5的随机模式对，实验中我们从两层BAM网络能够存储的39个模式对开始，逐步增加存储的模式对个数，这个例子中MR Ⅱ算法参数选择如下:δ=7,η=1,L=3.5。实验结果如表2所示，表中第一列为模式对个数，第二列为50次实验均能成功存储模式对需要的最少的中间层神经元个数，第三列为学习需要的平均迭代周期数。

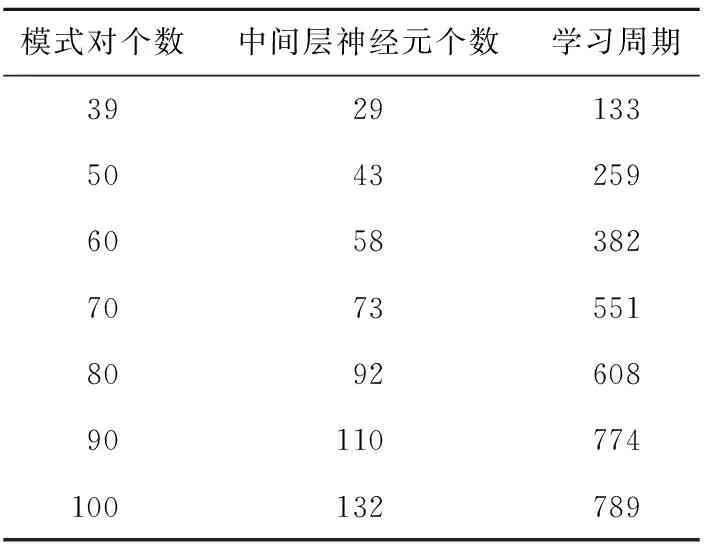
Table 2 Experimental results of TLBBAM learning 6×5 random model pairs

由表2可知，当存储的模式对个数为39个时，TLBBAM网络需要29个中间层神经元就可以成功存储所有模式对，此时需要的学习周期数平均为133，略多于QLBAM算法的。当存储的模式对个数不断增加，两层BAM网络已经不能成功存储所有模式，但是TLBBAM网络只要相应地增加中间层神经元个数就可以将所有模式对存储进网络。例如，当模式对个数为100时，中间层神经元个数增加到132个即可，此时网络的存储容量大概是两层BAM网络存储容量的2.5倍。由此可知，相比较两层BAM网络，TLBBAM网络极大地提高了存储容量。另外，理论上只要继续增加中间层神经元个数，网络中能够存储的模式对个数就会继续增加。由表2的第三列可知，伴随着存储容量的增加，TLBBAM网络需要的学习周期数也会增加。

对于BAM网络，针对学习算法的收敛性、网络存储容量以及算法学习效率的理论分析[13]是研究者普遍会讨论的内容。但是，TLBBAM有着自身的特点，首先，由于TLBBAM采用MR Ⅱ算法，而MR Ⅱ算法的一个显著特点就是不断地尝试翻转神经元的输出，这种试验性导致缺乏对其收敛性进行系统分析的理论基础。但是，这并不影响MR Ⅱ成为一种十分有效的学习算法。对于网络的存储容量，因为中间层神经元的个数不同，整个网络的存储容量也会不同，结合MR Ⅱ算法的特点导致TLBBAM网络的存储容量的理论分析会比较复杂，本文对此暂不考虑。但是，TLBBAM网络的存储容量具有很高的灵活性，通过增加中间层神经元个数就可以增加其容量，并且提高学习的成功率。

4 结束语

针对传统两层BAM存储能力不足的缺点，同时避免采用连续型神经元带来的问题，本文提出了一种三层二值BAM网络TLBBAM。该网络中的神经元使用硬极限函数作为激活函数，在处理二值问题时具有更高的效率和精度。TLBBAM网络通过增加中间层的方式在结构上扩展了传统的BAM网络，在学习方法上将MR Ⅱ算法应用于BAM网络首次实现了多层二值BAM网络的学习。实验表明，TLBBAM网络的模式存储和区分能力比传统两层BAM网络有极大的提高。今后的研究中我们将继续深入探讨TLBBAM网络的性质，如存储能力的分析、对带噪音模式的抗干扰能力以及网络参数的选择等等。

[1] Kosko B.Bidirectional associative memories[J].IEEE Transactions on Systems,Man and Cybernetics,1988,18(1):49-60.

[2] Maria E A-M,Cornelio Y M,Marco A A-M.Bidirectional associative memories:Different approaches[J].ACM Computing Surveys,2013,45(2):1-30.

[3] Sakthivel R,Vadivel P,Mathiyalagan K.Design of state estimator for bidirectional associative memory neural networks with leakage delays[J].Information Sciences,2015,296:263-274.

[4] Leung C S. Optimum learning for bidirectional associative memory in the sense of capacity[J].IEEE Transactions on Systems,Man and Cybernetics,1994,24(5):791-796.

[5] Oh H,Kothari S C.Adaptation of the relaxation method for learning in bidirectional associative memory[J].IEEE Transactions on Neural Networks,1994,5(4):576-583.

[6] Hattori M,Hagiwara M,Nakagawa M.New results of quick learning for bidirectional associative memory having high capacity[C]∥Proc of IEEE International Conference on Neural Networks,1994:1080-1085.

[7] Roukhe A,Fares A,Bouzid A.Multilayer neural network of adaptive bidirectional associative memories[J].Comptes Rendus de l’Acad′emie des Sciences-Series IIB-Mechanics-Physics-Astronomy,1999,327(7):691-699.

[8] Zhang W.MADALINE neural network with truncated momentum for LTV MIMO system identification[C]∥Chinese Control and Decision Conference,2012:23-25.

[9] Winter R,Widrow B.Madaline rule ii:A training algorithm for neural networks[C]∥Proc of IEEE International Conference on Neural Networks,1988:401-408.

[10] Sheng Xin-xin, Yan Wei-qiong, Wang Bing-hui.An improved learning algorithm for madaline network [J].Computer Technology and Development,2006,16(6):224-226.(in Chinese)

[11] Wang Fen,Wu Huai-yu.Existence and stability of periodic solution for BAM neural networks [J].Computer Engineering and Applications,2010,46(24):15-18.(in Chinese)

[12] Gao Ming.Stability of impulsive BAM neural networks with time-varying delays [J].Mathematica Applicata,2012,25(1):160-166.(in Chinese)

[13] Kabashima Y,Tanaka T,Kakiya S.Capacity analysis of bidirectional associative memory[C]∥Proc of International Conference on Neural Information Processing,2000:779-784.

附中文参考文献：

[10] 盛新新,颜伟琼,王炳辉.Madaline网络学习算法改进[J].计算机技术与发展,2006,16(6):224-226.

[11] 王芬,吴怀宇.BAM神经网络周期解的存在性与稳定性[J].计算机工程与应用,2010,46(24):15-18.

[12] 高明.变时滞脉冲BAM神经网络的稳定性[J].应用数学,2012,25(1):160-166.