基于均匀设计法的磨粒流加工试验
2018-03-06乔泽民张心明李俊烨卫丽丽赵伟宏
乔泽民 张心明 李俊烨 卫丽丽 赵伟宏
1.长春理工大学机电工程学院,长春,1300222.山西省计量科学研究院,太原,030032
0 引言
伴随着科技的进步与发展,机械加工由原始的粗加工逐步转向精密、超精密加工[1-2]。在所有的精密加工方法中,磨粒流加工(abrasive flow machining,AFM)是比较典型的一种精密加工方法,它可有效提高工件表面精度[3-4]。而在实际生产加工中,影响工件精度的因素众多,如何从大量的试验因素中选取最优的参数成为研究的重点[5-6],而均匀设计便可解决这一问题并可节省大量试验时间,节约成本。
均匀试验设计方法是基于“伪蒙特卡罗方法”的应用扩展而来的,其试验点的选取是基于总的试验范围从均匀性角度均匀散布的试验设计思路[7-9]。均匀设计是在试验范围的试验点中挑选部分代表性的试验点来进行设计的,在试验点的挑选上符合均匀分散、整齐可比性[10]。 “均匀分散”让每个有充分代表性的试验点都能均衡地分布在试验范围内,最终得到正确的指标;“整齐可比性”易于估计各因素的主效应和部分交互效应,对试验结果分析更为方便,能够分析出各因素对指标影响的大小及指标的变化规律。正交设计中,为了达到“整齐可比”,其试验点并未充分 “均匀分散”,只能选取较多的试验点数目,至少要做q2次试验(q为因素的水平数);而均匀设计的优势体现在试验范围大、水平数多的情形下,仍然能够极大地减少试验次数,只需要与因素水平数相等次数的q次试验即可,但不具备整齐可比性,其试验结果还需采用回归分析方法[11-12]处理。
本文利用均匀设计方法的试验点进行均匀布点,通过直接观察法选取出指标最好的试验条件组合,进而完成试验设计;或选取出最好的试验条件进行该条件小范围内试验测试,直到完成试验目标,从而结束试验[13]。
1 磨粒流加工试验及参数设计
1.1 试验对象及加工因素与参数
试验对象为坦克发动机喷油嘴。坦克发动机喷油嘴的作用是使柴油或汽油经喷油嘴内孔进入气缸,通过高压喷油,使油雾化,经火花塞点火燃烧,启动发动机,因此,对喷油嘴小孔加工精度要求非常高,其加工精度直接影响发动机喷射雾化和性能。
试验加工因素。在实际磨粒流加工过程中,影响磨削加工的因素很多,包括磨粒的选取(磨粒种类、磨粒粒径、磨粒浓度(质量分数)等)、加工时间、挤压压力、研磨系统初始温度等,而在众多参数中,能够明显影响加工效果的主要有加工时间、磨粒粒径、磨料浓度等工艺参数。在其他超精密加工方法中,如电解池加工,液体PH值会对加工产生明显的影响,而在磨粒流加工中人们还未对此因素进行研究,因此,选取研磨液PH值作为试验的因素来探究其是否对磨粒流加工效果产生影响。在均匀设计中,指标是检验试验加工的依据,而磨粒流加工要实现加工零件内表面的去毛刺和倒圆角的目标,能够检验加工效果的最佳指标是表面粗糙度,故选取表面粗糙度作为检验指标。
在试验过程中,每种因素各取10个水平:磨料浓度2%、4%、6%、8%、10%、12%、14%、16%、18%、20%,磨粒粒径2.5 μm、3.5 μm、5.5 μm、6.5 μm、7 μm、8 μm、10 μm、14 μm、28 μm、40 μm,PH值3、4、5、6、7、8、9、10、11、12,加工时间30 s、60 s、90 s、120 s、150 s、180 s、210 s、240 s、270 s、300 s,参数数据选取方面比较均匀,水平数较多,能够合理反映出试验所要达到的目标。均匀设计参数对照表见表1。
1.2 磨粒流加工试验进程
在进行磨粒流试验前,根据所选取的加工因素,进行磨料浓度比例的调配,磨粒选取绿碳化硅磨粒,用托盘天平进行磨粒的称量。根据颗粒粒径的不同进行研磨液的调配,采用PH调制仪进行研磨液PH值调节。
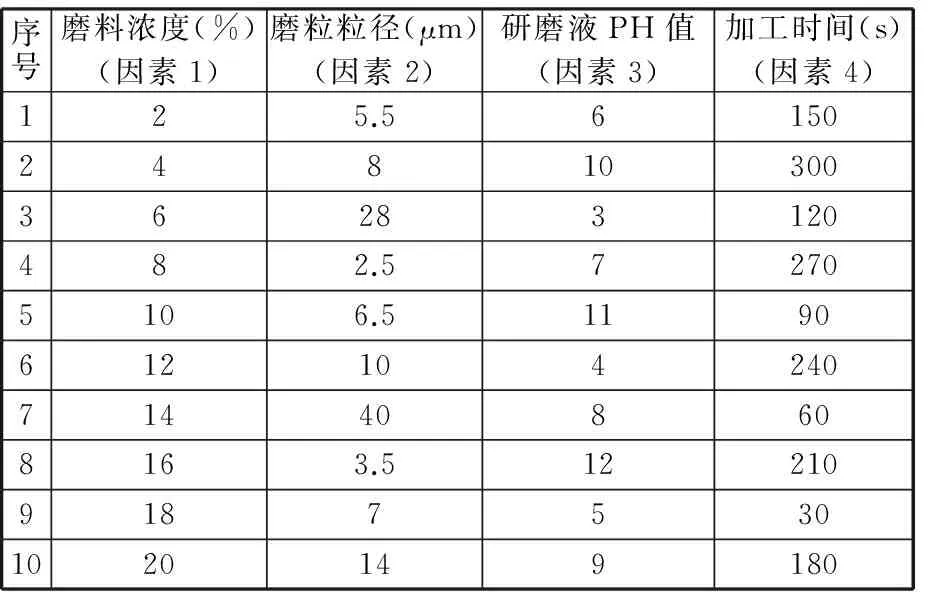
表1 磨粒流加工试验参数对照表
依据均匀试验参数进行磨粒流加工试验,只进行10组试验,分别记作样件01,样件02,……,样件10,试验过程中应注意磨料缸的清洗,去除磨粒对液压缸壁面的黏附及PH值对下一组试验加工的影响。
为进行磨粒流加工后的表面质量检测,需对切割后的喷油嘴工件进行清洗。把工件放入20 kHz超声振荡仪内,加入少许氧化锌、酒精进行工件表面污渍的去除并防氧化,之后放入烤箱内对零件烘干,去除零件水渍,达到检测标准后,再进行相关检测。
1.3 磨粒流加工结果
对10组零件进行磨粒流加工后,需超声波清洗并进行线切割,使之达到测试标准。利用Mahr触针测量仪对表面粗糙度Ra进行精准的接触式测量,测量结果如图1所示。
经过上述检测,得到原件01、02及样件01,02,…,10的表面粗糙度,具体数值见表2。由图1和表2可知,原件01和原件02表面粗糙度Ra测量结果为1.959 μm和1.975 μm,加工后的各样件测试结果显示Ra值波动较小,测量结果最大为0.882 μm,最小为0.545 μm,其中,样件06和样件09的Ra值波动最平稳,上下跳跃幅度最小(图1h、图1k),其Ra值也最小,测量结果为0.592 μm和0.545 μm,加工精度提高了1 μm左右,证实了磨粒流加工的有效性。
2 磨粒流加工多元回归模型的建立
采用均匀试验设计法进行试验,通过磨粒流加工试验获得理想的试验结果,该试验方法具备均匀分散性而不具备整齐可比性,故不能直接判断水平参数的优劣并做出分析,因此,采用多元回归分析方法进行试验数据的分析。

(a)原件01表面粗糙度(b)原件02表面粗糙度

(c)样件01表面粗糙度(d)样件02表面粗糙度

(e)样件03表面粗糙度(f)样件04表面粗糙度

(g)样件05表面粗糙度(h)样件06表面粗糙度

(i)样件07表面粗糙度(j)样件08表面粗糙度

(k)样件09表面粗糙度(l)样件10表面粗糙度图1 试验工件的粗糙度检测结果Fig.1 Inspection results roughness of the test workpiece
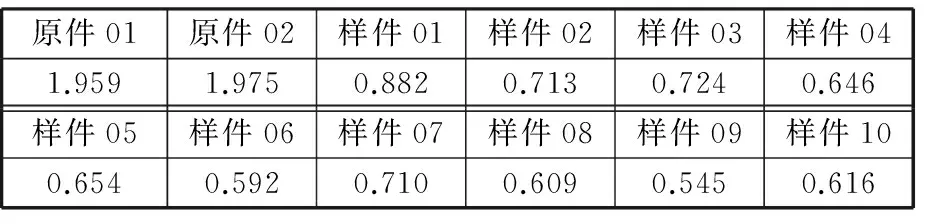
原件01原件02样件01样件02样件03样件041.9591.9750.8820.7130.7240.646样件05样件06样件07样件08样件09样件100.6540.5920.7100.6090.5450.616
2.1 表面粗糙度数学模型的建立
根据均匀试验设计方法的设计理论,表面粗糙度数学模型的回归分析选用全回归法设计,拟建立表面粗糙度与材料物性及加工时间的数学模型为
y=b(0)+b(1)lgX(1)+b(2)X(2)+
b(3)X(3)+b(4)X(4)
(1)
其中,y表示指标量(表面粗糙度),X(1)、X(2)、X(3)、X(4)分别表示因素1(磨料浓度)、因素2(磨粒粒径)、因素3(PH值)及因素4(加工时间),回归系数b(i)结果如下:
(2)
由回归系数b(i)的结果,可以得到标准回归系数B(i):
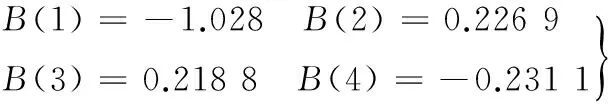
(3)
联立式(1)和式(2),由回归方程及系数b(i)的值,进一步简化,即可得到表面粗糙度与材料物性及加工时间的数学模型(非线性模型):
y=0.913 7-0.305 4lgX(1)+1.701×10-3X(2)+
6.833×10-3X(3)-2.406×10-4X(4)
(4)
由式(4)可知,当选取4种因素的任意组合时均可求得喷油嘴工件的表面粗糙度。
2.2 回归显著性检验
建立表面粗糙度数学模型之后,需要进一步研究因变量y取值的变化规律,即进行回归方程显著性检验,由以上分析可得到变量分析表,见表3。
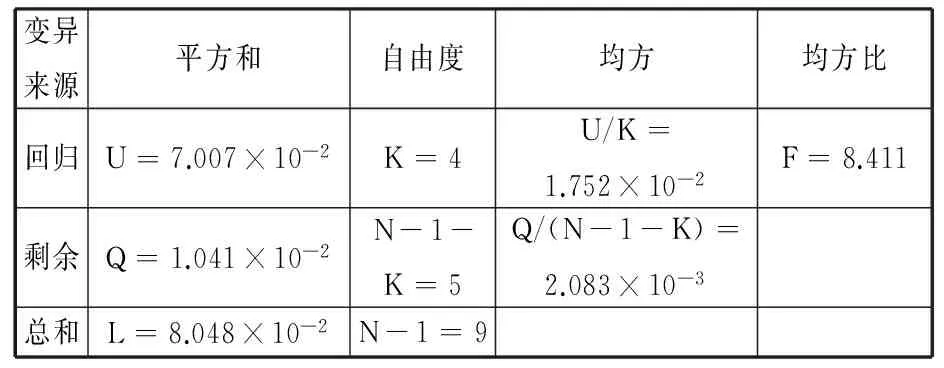
表3 变量分析表
由表3可得检验值Ft=8.411,当检验值大于临界值时,回归方程显著,此时的显著性水平α=0.05,得到临界值F(0.05,4,5)=5.192,易得Ft>F(0.05,4,5),即回归方程显著。
4个自变量对回归方程总体回归均有效,但并不是4个自变量对回归结果值都是关键的,因此,某一个或两个变量对加工结果并没有作用或作用很小,希望将这种自变量从回归中剔除,则可建立更简单的回归方程。计算各方程项对回归结果的贡献值,从高到低排序,贡献值计算结果如下:
(5)
其中,磨料浓度U(1)对回归的贡献最大,其次是加工时间U(4),再次是磨粒粒径U(2),而研磨液PH值U(3)对回归的贡献最小。对因素3进行显著性检验:检验值F(3)=1.465,临界值F(0.05,1,5)=6.608,因此F(3)≤F(0.05,1,5),即检验值小于临界值,研磨液PH值因素不显著。
通过以上对回归方程显著性检验,其结果显著;对回归系数进行显著性检验,其第3项因素不显著,故可以忽略,由此可得简化后的数学模型:
y=0.913 7-0.305 4lgX(1)+1.701×10-3X(2)-
2.406×10-4X(4)
(6)
综上,通过多元回归分析,最终得到简化后的表面粗糙度与材料物性及加工时间的数学模型,研磨液PH值对粗糙度的影响最小。对参数进行优化后,可用式(6)计算优化后参数组合的表面粗糙度,进而与试验结果进行对比,检测该模型是否正确可信。
3 磨粒流加工参数优化及模型验证
通过对以上试验因素的分析,进而进行磨粒流加工参数优化,在选取相应的数值多元回归分析后,建立表面粗糙度与材料物性及加工时间回归模型,进而可以得到残差数值,残差分析表见表4。

表4 残差分析表
本试验选取网格尝试法作为优化计算的方法,对各因素的所有水平组合进行分析,进而求得试验结果,由此得到各因素的最优试验条件组合。只要将各试验条件的水平数(此时的水平数指依据回归方程进行数值计算时用的水平数,而不是实际试验过程中的各因素水平数,可以比试验中所选取的水平数大很多,水平数越多,划分越细致,可供选择点越多)划分得足够细,就可找到满意的优化条件,条件优化设置及最佳试验条件见表5。
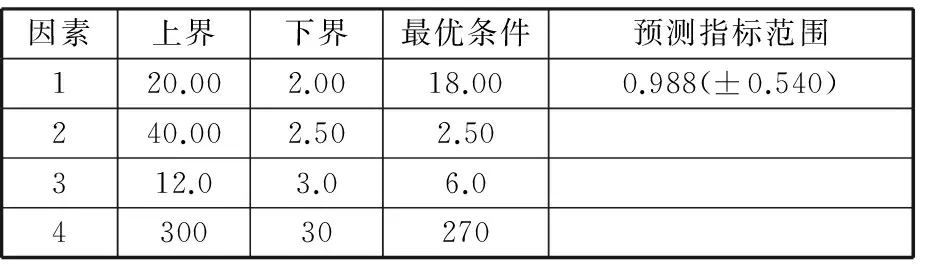
表5 条件优化设置及最佳试验条件
由表5所得的最佳优化结果,选取该参数组合代入式(6)进行分析,得到表面粗糙度y=0.469 μm,远低于实际测量的最小值0.545 μm,证明优化的模型正确合理。
为了验证表面粗糙度模型的正确性,需要通过最优条件得到的参数进行加工试验,因此,选取该水平参数如下:磨料浓度为18%,磨粒粒径为2.5 μm,研磨液PH值为6,加工时间为270 s,根据此组优化参数进行磨粒流加工试验。经过检测,喷油嘴小孔表面粗糙度测试结果为0.473 μm,如图2所示,可以看出,经过优化之后表面粗糙度与材料物性及加工时间的数学模型的预测结果0.469 μm与实际检测值0.473 μm非常接近,验证了优化模型的精确性和数学模型的正确性及均匀试验设计方法的准确性,证实了试验测试结果完全与理论计算相符合,能够为实际生产加工提供指导。

图2 粗糙度测量结果Fig.2 Roughness measurement results
4 结论
(1)喷油嘴试验工件经过磨粒流加工之后表面粗糙度的检测结果均比原件的表面粗糙度小,且10组试验中第9组试验样件的表面粗糙度最低,达到0.545 μm。
(2)对各因素的回归贡献进行分析后发现,研磨液酸碱性贡献最小,忽略后得到了简化后的数学模型。
(3)进行参数优化,得到优化后的参数组合(磨粒浓度为18%、磨粒粒径为2.5 μm,PH值为6及加工时间为270 s),经磨粒流加工试验验证后,所测得的表面粗糙度值(0.473 μm)与模型求得的表面粗糙度值(0.469 μm)近似相等,证实了表面粗糙度与材料物性及加工时间的数学模型的正确性。
[1] 李俊烨,许颖,杨立峰,等.基于非直线管的磨粒流加工实验分析[J].中国机械工程,2014,25(13):1729-1734.
LI Junye, XU Ying, YANG Lifeng, et al. Experimental Analysis of Abrasive Flow Machining Based on Non Linear Tube [J]. China Mechanical Engineering,2014,25(13): 1729-1734.
[2] 计时鸣,唐波,谭大鹏,等.结构化表面软性磨粒流精密光整加工方法及其磨粒流动力学数值分析[J].机械工程学报,2010,46(15):178-184.
JI Shiming, TANG Bo,Tan Dapeng, et al. Structured Surface Soft Abrasive Flow Numerical Analysis of Precisionfinishing Method and Abrasive Flow Mechanics [J].Journal of Mechanical Engineering, 2010,46(15): 178-184.
[3] 丁金福, 刘润之, 张克华,等. 磨粒流精密光整加工的微切削机理[J]. 光学精密工程, 2014,22(12): 3324-3331
DING Jinfu, LIU Runzhi, ZHANG Kehua, et al. Micro Cutting Mechanism of Abrasive Flow Precision Machining[J]. Optics and Precision Engineering, 2014, 22(12): 3324-3331.
[4] 计时鸣,黄希欢,谭大鹏,等. 气-液-固三相磨粒流光整加工及其工艺参数优化[J]. 光学精密工程, 2016,24(4): 855-864.
JI Shiming, HUANG Xihuan, TAN Dapeng, et al. Gas-liquid-solid Abrasive Flow Polishing and Its Process Parameter Optimization[J]. Optics and Precision Engineering, 2016, 24(4): 855-864.
[5] 高航,付有志,王宣平,等.螺旋面磨料流光整加工仿真与试验[J].浙江大学学报(工学版),2016,50(5):920-926.
GAO Hang,FU Youzhi,WANG Xuanping,et al.Helicoid Grinding Time Whole Process Simulation and Experiment[J].Journal of Zhejiang University (Engineering Science),2016,50(5):920-926.
[6] LI Junye, LIU Weina, YANG Lifeng,et al.Study of Abrasive Flow Machining Parameter Optimization Based on Taguchi Method[J].Journal of Computational and Theoretical Nanoscience, 2013, 10(12): 2949-2954.
[7] 方开泰,王元.均匀设计与均匀设计表[M].北京:科学出版社,1994:1-20.
FANG Kaitai, WANG Yuan. Uniform Design and Uniform Design Table [M]. Beijing: Science Press, 1994: 1-20.
[8] 李响,李为吉,彭程远.基于均匀试验设计的响应面方法及其在无人机一体化设计中的应用[J].机械科学与技术,2005,24(5):575-577.
LI Xiang, LI Weiji, PENG Chengyuan. Response Surface Methodology Based on Uniform Test Design and Its Application in the Integrated Design of UAV [J]. Mechanical Science and Technology, 2005,24 (5): 575-577.
[9] 邱建新,张士宏,李国禄,等.均匀设计法/神经网络和遗传算法结合在内高压成形工艺参数优化中的应用[J].塑性工程学报,2005,12(4):76-79.
QIU Jianxin, ZHANG Shihong, LI Guolu,et al. Uniform Design Method / Neural Network and Genetic Algorithm Combined with the Application of Internal High Pressure Forming Process Parameters Optimization [J].Journal of Plasticity Engineering, 2005,12 (4): 76 - 79.
[10] 吕大刚,贾明明,李刚.结构可靠度分析的均匀设计响应面法[J].工程力学,2011,28(7):109-116.
LYU Dagang, JIA Mingming, LI Gang. Structural Reliability Analysis of Uniform Design Response Surface Method [J]. Engineering Mechanics, 2011,28 (7): 109-116.
[11] 于昌龙,张红线,吴衍记.基于均匀设计的光纤陀螺温度建模实验方案研究[J].红外与激光工程,2009, 38(2): 330-334.
YU Changlong, ZHANG Hongxian, WU Yanji. Experimental Study on Temperature Modeling of Fiber Optic Gyroscope Based on Uniform Design [J].Infrared and Laser Engineering, 2009,38(2): 330-334.
[12] 李忠群,刘强.圆角铣削颤振稳定域建模与仿真研究[J].机械工程学报,2010,46(7):181-186.
LI Zhongqun, LIU Qiang. Modeling and Simulation of Chatter Stability for Circular Milling[J]. Journal of Mechanical Engineering, 2010,46 (7): 181-186.
[13] 李登万,陈洪涛,许明恒,等.基于均匀设计法的钛合金切削参数优化试验研究[J].机械科学与技术,2011,30(5):689-692.
LI Dengwan, CHEN Hongtao, XU Mingheng, et al. A Test Study of the Cutting Parameters Optimization of Titanium Alloy Based on Uniform Design Method[J]. Mechanical Science and Technology for Aerospace Engineering,2011,30(5):689-692.
