滚珠丝杠进给系统滚动结合部径向动态特性参数辨识

朱坚民 郑洲洋 胡育佳 周亚南

上海理工大学机械工程学院，上海，200093

0 引言

滚珠丝杠进给系统是数控机床的关键组成部分，它由滚珠丝杠、滚动导轨、轴承、工作台、丝杠螺母等零部件通过不同类型的结合部连接而成。滚珠丝杠属于细长杆件，使得进给系统的径向刚度小于其轴向刚度，系统径向更容易产生较大振动，降低机床加工精度。研究表明，滚动结合部径向动态特性参数是影响进给系统动力学性能的重要因素[1]，准确辨识滚珠丝杠进给系统滚动结合部的径向动态特性参数对提高机床加工精度、评估进给系统性能及装配精度具有重要意义。

滚珠丝杠进给系统存在两种类型的结合部，即螺栓连接的固定结合部和滚动导轨副、两端轴承组、滚珠丝杠副滚动结合部。对于进给系统滚动结合部径向参数辨识的研究，多数文献通常忽略了滚珠丝杠副的径向动态特性参数，而IGARASHI等[2]、王建文[3]的滚珠丝杠进给系统动态性能试验表明，滚珠丝杠副径向刚度对进给系统动力学特性有重要影响，忽略径向刚度将不能满足其动力学研究需要。陈勇将等[4]也指出滚珠丝杠副径向刚度和外部载荷、倾覆力矩等影响因素有直接关系。

目前，进给系统滚动结合部径向动态特性参数辨识方面的研究主要可归纳为两大类。第一类是针对单个结合部的参数辨识，即单独搭建滚动导轨副、滚珠丝杠副或轴承的实验台，运用理论分析法、实验法或理论分析与实验结合等方法确定单个滚动结合部的动态特性参数。如李松生等[5]基于滚动轴承受力分析的拟静力学和拟动力学，模拟计算了电主轴轴承对转子的径向动态支撑刚度；芮红锋等[6]基于共振法原理，采用轴承组件的方法识别和测试轴承径向动态刚度和阻尼参数；HU等[7]通过实验测试与理论计算相结合的方法识别了轴承的径向动态特性参数；毛宽民等[8]利用刚度影响系数法建立导轨动力学模型，通过实验模态分析与有限元分析相结合的手段辨识出导轨副法向动态特性参数；DHUPIA等[9]基于赫兹接触理论及二维切比雪夫多项式拟合法，建立直线滚动导轨结合部动态特性参数辨识模型，得到导轨副法向动态特性参数。这些研究虽能准确辨识单个滚动结合部的径向动态特性参数，但整机状态下进给系统滚动结合部参数识别受装配间隙、摩擦、预紧力等条件影响较大，难以准确辨识进给系统滚动结合部径向刚度和阻尼。

第二类是在进给系统整机状态下进行参数辨识。如蒋书运等[1]借助于弹性力学中赫兹接触理论，计算进给系统滚动结合部的径向刚度，并着重讨论了工作载荷对结合部动态刚度的影响规律；叶健等[10]依据机械阻抗原理，提出一种有限元计算与实验测试相结合的方法，得到进给系统径向刚度与阻尼参数。在以上第二类滚动结合部径向参数辨识研究中均将丝杠简化为刚体，但丝杠具有长径比大、刚性低等特点，其截面弯曲振动情况沿轴向存在较大差异，故将丝杠简化为刚体会产生较大的建模误差，且目前对进给系统在整机状态下的研究多为动力学建模与动态特性分析[11-13]，对其滚动结合部径向参数辨识的研究较少。针对上述问题，本文提出了进给系统整机状态下滚动结合部径向动态特性参数辨识新方法。

1 进给系统径向动力学模型

数控机床上滚珠丝杠进给系统的典型结构如图1所示。交流伺服电机通过联轴器带动丝杠转动，再通过丝杠螺母副将旋转运动转化为直线运动，从而实现工作台沿着滚动导轨直线进给。丝杠两端分别由左右滚动轴承组支撑，丝杠螺母通过螺母座与工作台相连接。

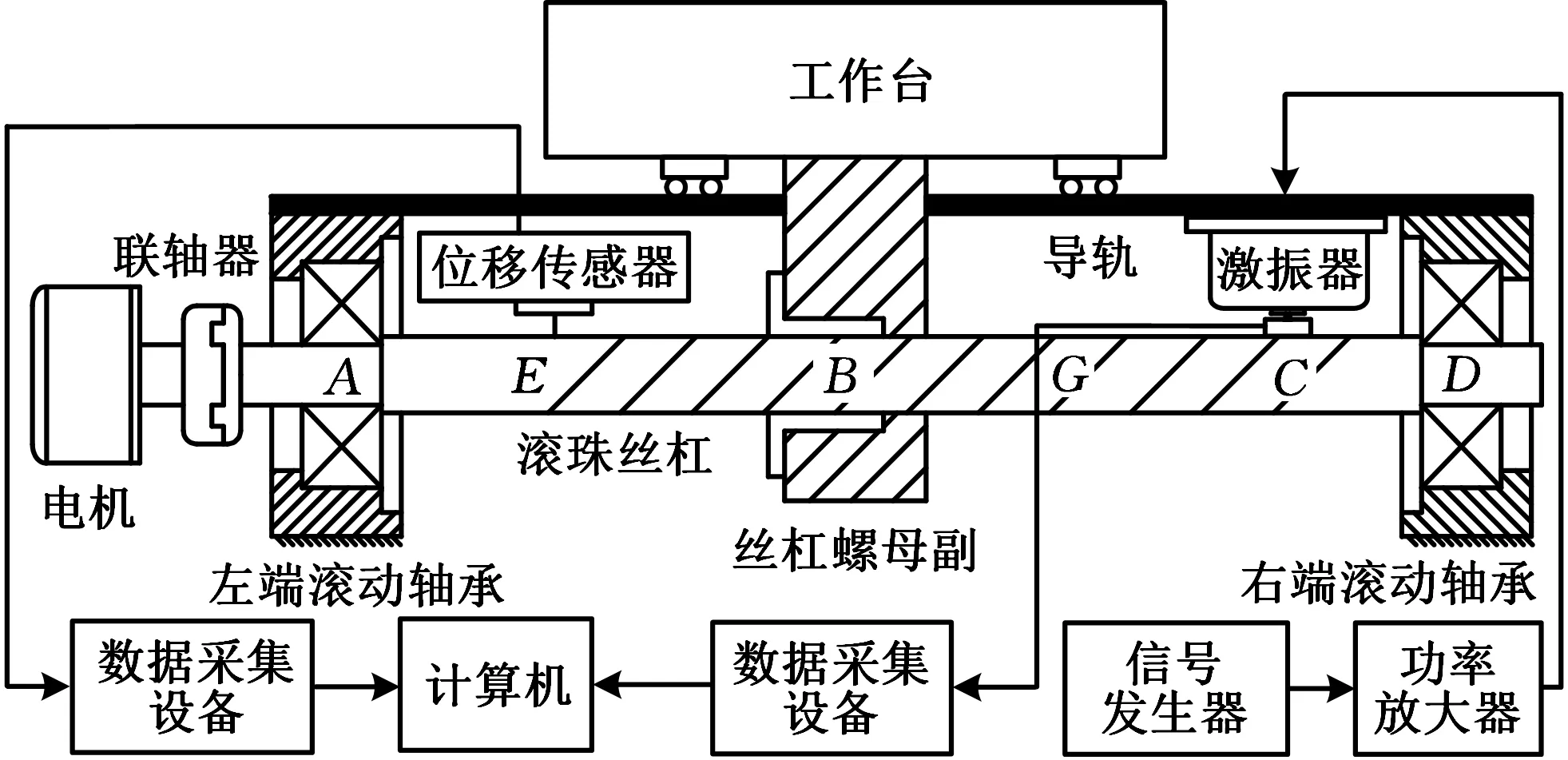
图1 滚珠丝杠进给系统结构示意图Fig.1 Structure diagram of ball screw feed system

工作台、左右两端轴承座和床身均可简化为刚体；相对于滚动结合部，栓接固定结合部刚度和阻尼很大，可简化为刚性连接；左端轴承组、右端轴承组、滚珠丝杠副和滚动导轨副可简化为径向弹簧-阻尼单元。细长的丝杠在径向简谐激振力F的作用下，丝杠各点的径向振动情况不同，本文将丝杠简化为欧拉-伯努利梁，建立图1进给系统的径向动力学模型如图2所示。

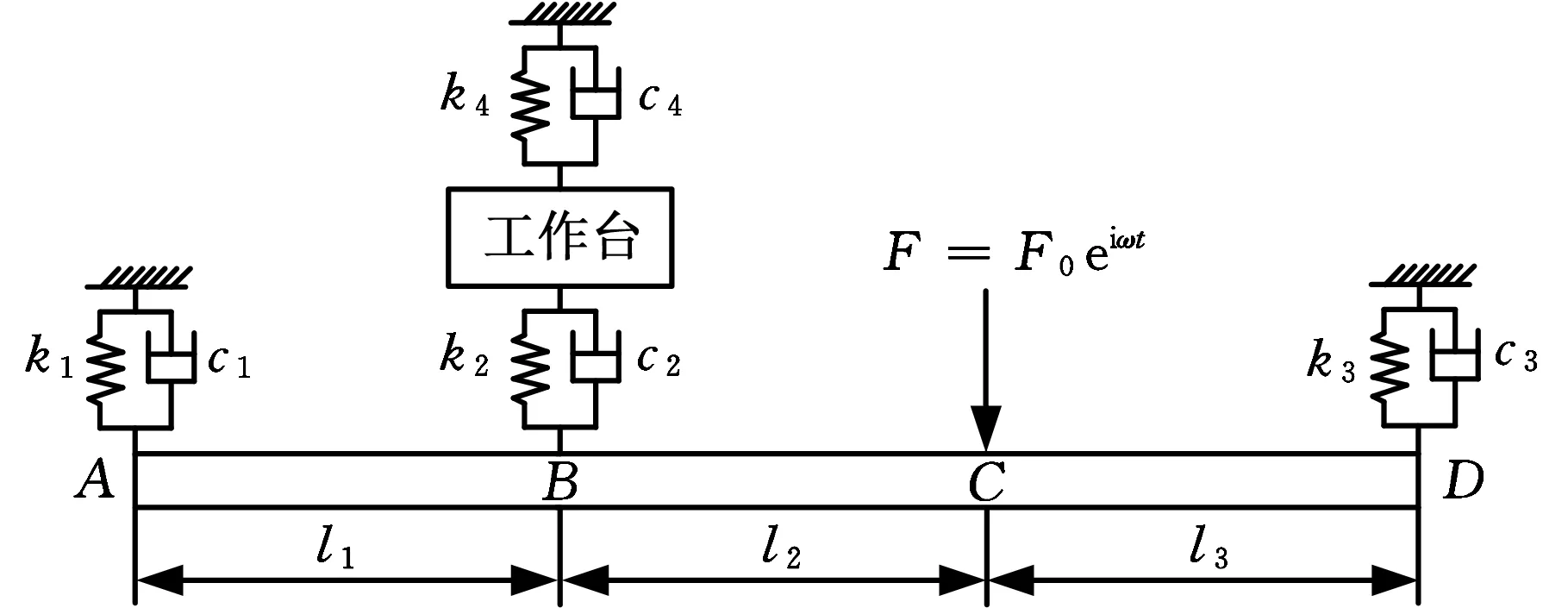
图2 进给系统径向动力学模型Fig.2 Radial dynamics model of feed system

图2中丝杠AD的左端轴承组、滚珠丝杠副、右端轴承组和滚动导轨副的径向刚度和径向阻尼分别为k1、c1、k2、c2、k3、c3、k4、c4；为确定这些参数，需在丝杠上施加径向简谐激振力F=F0eiωt(F0为幅值，ω为角频率)，见图2中C点上作用力；丝杠上左端轴承组、丝杠螺母、激振点和右端轴承组的等效支撑点分别设为A、B、C、D，A和B、B和C、C和D之间距离分别为l1、l2、l3。

2 丝杠各截面径向振动方程

图2中，因B、C两点受到外力作用，为建立丝杠沿轴向上各截面的径向振动方程，将丝杠分为五部分，依次标记为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ，如图3所示。各相邻部分连接截面的振动位移、转角、剪力、弯矩连续，并将B点左侧截面以及Ⅰ的右端截面记为BL，B点右侧截面以及Ⅲ的左端截面记为BR，C点左侧截面以及Ⅲ的右端截面记为CL，C点右侧截面以及Ⅴ的左端截面记为CR。因Ⅱ、Ⅳ两段丝杠的轴向长度均为零，为求得丝杠各截面的径向振动位移方程，只需求解Ⅰ、Ⅲ、Ⅴ部分丝杠的径向振动位移方程即可。本文对Ⅰ、Ⅲ、Ⅴ部分分别建立坐标系,来求解这三部分的径向振动位移方程。

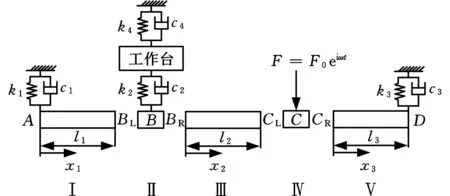
图3 进给系统径向力学分段模型Fig.3 Sectional model of radial mechanics for feed system

2.1 Ⅰ、Ⅲ、Ⅴ的径向振动位移方程

图3中，丝杠在简谐力F作用下Ⅰ、Ⅲ、Ⅴ三部分均遵循梁的弯曲振动理论。以Ⅰ部分为例，以A点为坐标原点，以丝杠轴向为x1轴，x1∈[0,l1]，建立Ⅰ部分丝杠的弯曲振动方程。设此段丝杠上任意一点到A点的轴向距离为x1，丝杠在简谐激振力F作用下，Ⅰ部分丝杠上任意一点相对于A点的弯曲振动方程为

(1)

0≤x1≤l1

式中，u(x1,t)为丝杠上x1点径向振动位移，它是距离x1与时间t的二元函数；I、E、m分别为丝杠的截面惯性矩、弹性模量、线密度。

由于丝杠在简谐力作用下发生受迫简谐振动，丝杠上各点径向振幅不同，故u(x1,t)可表示为

u(x1,t)=U(x1)eiωt

(2)

式中，U(x1)为丝杠径向振型函数。

将式(2)代入式(1)可得

(3)

式(3)的通解可表示为

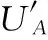
(4)

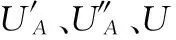
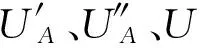
(5)

(6)

(7)

将式(5)～式(7)代入式(4)可得到Ⅰ部分丝杠上任意一点的径向振动位移方程：

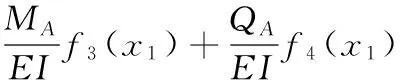
(8)

0≤x1≤l1

由式(3)～式(8)可得

(9)

(10)

(11)

(12)

同理，Ⅲ部分丝杠在简谐力F作用下，以BR为坐标原点，以丝杠轴向为x2轴，x2∈[0,l2]，可得到Ⅲ部分丝杠上任意一点的径向振动位移方程：

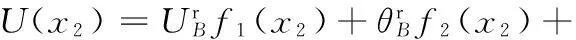
(13)

0≤x2≤l2

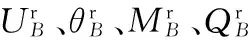
同理，Ⅴ部分丝杠在简谐力F作用下，以CR为坐标原点，以丝杠轴向为x3轴，x3∈[0,l3]，得到Ⅴ部分丝杠上任意一点的径向振动位移方程：

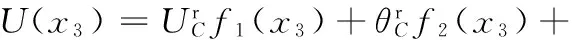
(14)

0≤x3≤l3

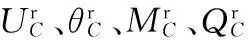
为建立以A点(UA、θA、MA、QA)为基点的整个丝杠所有截面径向振动方程，本文通过建立丝杠截面A、截面BL、截面BR、截面CL、截面CR、截面D之间的振动位移矩阵关系式，最终将k1、c1、k2、c2、k3、c3、k4、c4包含到整段丝杠所有截面的径向振动方程中。

2.2 各部分丝杠端面振动矩阵关系式

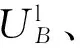
(15)

式(15)简记为

(16)

同理，当x2=l2时，可得出Ⅲ部分丝杠两端面的振动矩阵关系式：

(17)

式(17)简记为

(18)

当x3=l3时，可得出Ⅴ部分丝杠两端面的振动矩阵关系式：

(19)

式(19)简记为

(20)

对于Ⅱ部分丝杠，为获得与Ⅰ、Ⅲ、Ⅴ三部分形式相同的振动矩阵关系式，对B点左右侧滚珠丝杠受力进行分析，其径向力学模型如图4所示。

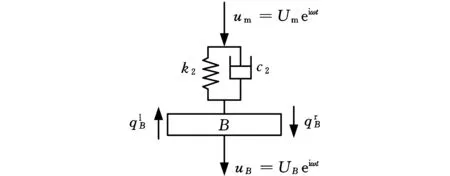
图4 丝杠B点左右两侧端面径向力学模型Fig.4 Radial mechanical model of the left and rightside ends of B point of the screw

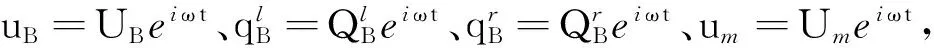
(21)

得

(22)

再对工作台进行受力分析，其径向力学模型如图5所示。

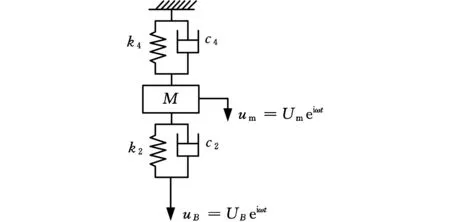
图5 工作台径向力学模型Fig.5 Radial mechanics model of worktable

工作台的径向振动微分方程为

(23)

式中，M为工作台质量。

将uB=UBeiωt、um=Umeiωt代入式(23)，可得

(24)

由式(22)、式(24)可得出丝杠Ⅱ部分两端截面的矩阵关系式为

(25)

式(25)简记为

(26)

由式(25)可知，丝杠上一点在受外力作用时，其左右侧截面的径向振动位移、转角和弯矩相同，只有剪力不同。因此对于Ⅳ部分丝杠上受力F=F0eiωt作用的C点，可直接确定丝杠Ⅳ部分两端截面的矩阵关系式为

(27)

式(27)简记为

(28)

结合式(8)、式(13)～式(20)、式(25)～式(28)，丝杠各截面的径向振动方程可表示为

U(x)=

(29)

式(29)是以UA、θA、MA、QA为系数，以x为变量的方程，其中x为丝杠AD上任意一点到A点的轴向距离。

2.3 UA、θA、MA、QA的确定

由式(16)、式(18)、式(20)、式(26)和式(28)可得

PD=T4T3T2T1PA-T4TF

(30)

令

(31)

故式(30)可写成

(32)

由A点处边界条件可得

(33)

由D点处边界条件可得

(34)

联立式(32)～式(34)，以UA、UD和θA为未知量，解三元一次方程组，得

UA=a/b

(35)

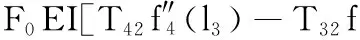
(36)

b=(EI)2(T41T32-T42T31)+EI(k1+iωc1)(T44T32-
T42T34)+EI(k3+iωc3)(T12T31-T11T32)+(k1+iωc1)(k3+iωc3)(T12T34-T14T32)

(37)

(38)

3 参数辨识

本文参数辨识基本原理流程图见图6。在丝杠AB段任取一点E，作为电涡流位移传感器测量点，由式(29)可计算E点的径向振动位移理论计算值；设计实验获得该点的径向振动位移实验测试值；以E点的径向振动位移理论计算值与实验测试值建立目标函数，基于人工鱼群算法[14-16](artificial fish swarm algorithm，AFSA)优化识别出进给系统滚动结合部的径向刚度及径向阻尼参数。

图6 参数辨识基本原理流程图Fig.6 Flow chart of basic principle of parameter identification

令E点到A点的轴向距离为l,即x=l，0≤l≤l1则由式(29)、式(33)可得出E点径向振动位移幅值解析式为

(39)

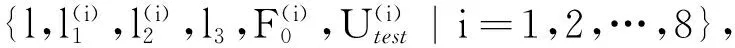
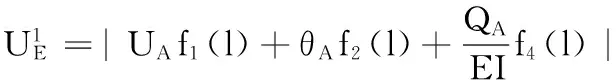
由上式可知该方程组未知量较多且较复杂，用传统变量消元法、代入法等求解较困难。本文将该求解问题转化为参数优化问题，用AFSA[17]求解。AFSA算法非常适用于数值变化范围较大的动态特性参数辨识。本文用AFSA求解以上八元一次方程组，具体优化求解中的相关说明如下：

(1)优化变量。以k1、c1、k2、c2、k3、c3、k4、c4为优化变量，记为Φ={k1，c1；k2，c2；k3，c3；k4，c4}。

(2)目标函数。以丝杠测量点E点径向振动位移幅值的理论计算值Ucal与其实验测试值Utest建立优化目标函数，即

(40)

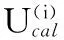
(3)约束条件。参数辨识区间的设定会影响辨识速度和精度，尤其在设置参数辨识的初始区间时，应适当放大区间范围，以免遗漏最优解。根据已有文献的研究成果，滚动结合面刚度参数范围一般为104～109N/m，阻尼参数范围一般为10～107N·s/m，因此本文的刚度参数辨识初始区间设为102～1011N/m，阻尼参数辨识初始区间设为1～109N·s/m。

(4)食物浓度函数。该函数用于计算鱼的当前位置食物浓度函数值，值越大则鱼的数量越多。据式(40)优化问题的目标函数，个体目标函数值越小食物浓度越大，建立食物浓度函数：

AFf=1/y(Φ)

(41)

(5)收敛准则。设置最大迭代代数终止算法操作。

基于MATLAB语言编制求解程序，便可求出进给系统滚动结合部径向动态特性参数。

4 实验研究

4.1 实验原理

以自行研制的滚珠丝杠进给实验台(图7)为研究对象，用本文方法对滚珠丝杠副、滚动导轨副以及两端滚动轴承组结合部的径向动态特性参数进行辨识。采用图1所示的实验测试方案，信号发生器输出简谐激励信号，通过功率放大器驱动激振器做简谐振动，采用刚度很小的橡皮绳竖直悬挂激振器，使壳体保持静止不动的情况下对丝杠进行激振。激振器的激振杆端部自带力传感器，采用数据采集设备采集激振力信号。采用电涡流传感器测量丝杠上E点径向振动位移幅值，实验中所用设备及型号见表1。

图7 滚珠丝杠进给实验台Fig.7 Ball screw feed experiment table

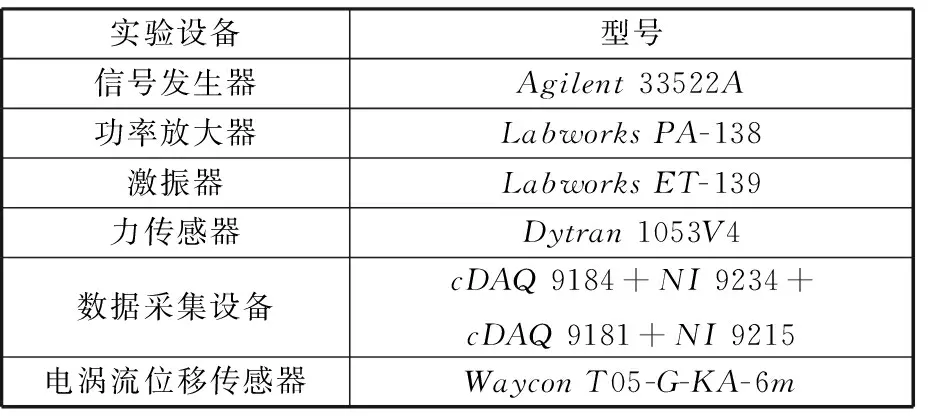
实验设备型号信号发生器Agilent33522A功率放大器LabworksPA-138激振器LabworksET-139力传感器Dytran1053V4数据采集设备cDAQ9184+NI9234+cDAQ9181+NI9215电涡流位移传感器WayconT05-G-KA-6m

4.2 实验方案

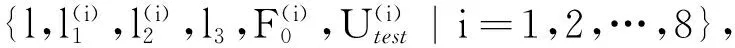
实验时，基于LabVIEW软件平台编制数据采集程序，采用NI 9234板卡采集激振力信号，同时采用NI 9215板卡采集E点的振动位移信号。

4.3 实验结果

将表2、表3中数据导入鱼群算法MATLAB程序中，识别所得滚动结合部径向刚度、阻尼参数见表4。

4.4 参数辨识验证

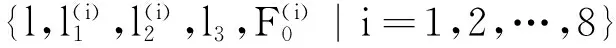
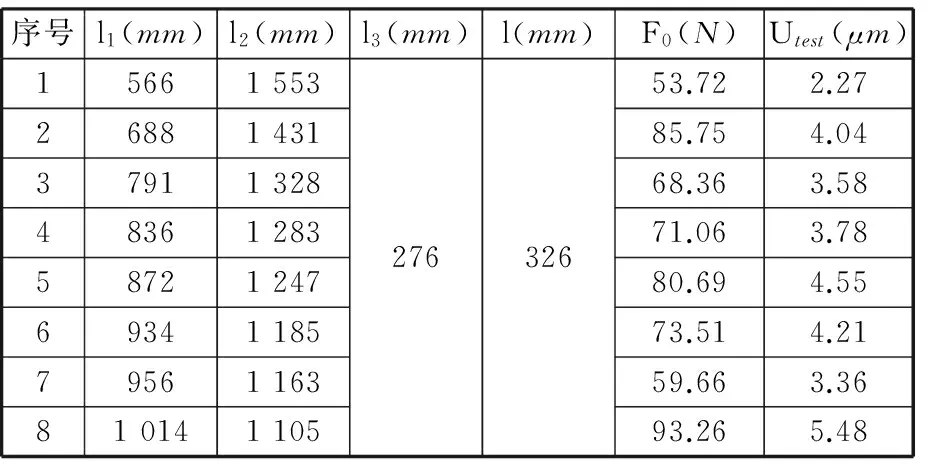
表2 实验数据

表3 丝杠、工作台基本参数

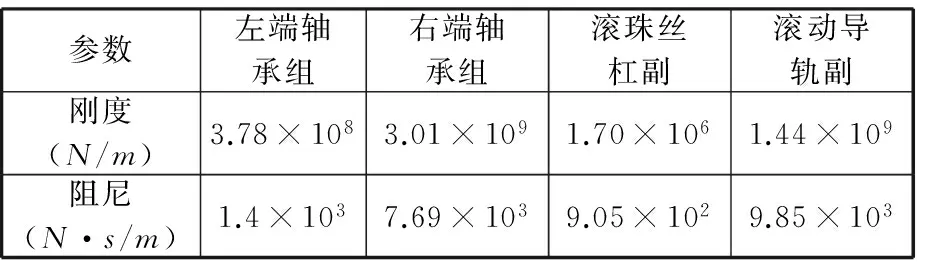
表4 径向刚度、阻尼参数辨识结果

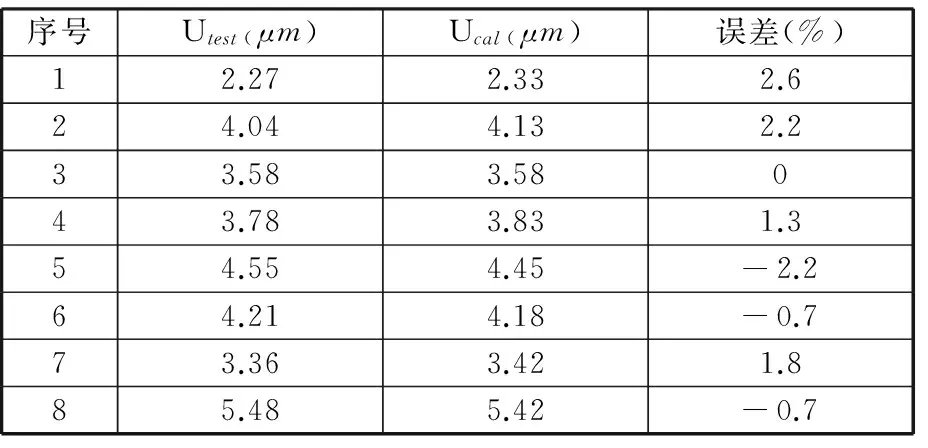
表5 E点径向位移的实验值与计算值的比较

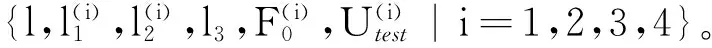
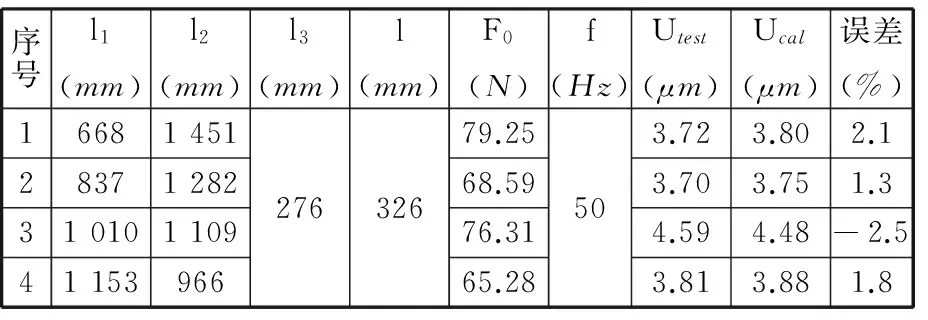
表6 激振频率为50 Hz时E点径向振动位移实测值与计算值

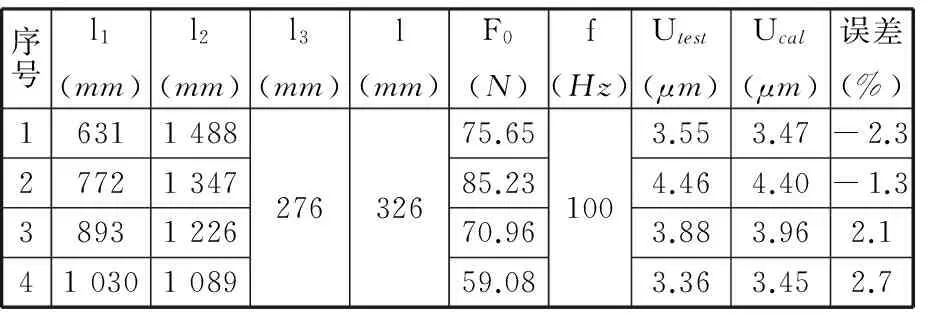
表7 激振频率为100 Hz时E点径向振动位移实测值与计算值

为进一步验证本文方法的正确性，在工作台右侧丝杠Ⅲ部分上任取一点G作为新的振动位移测量点，G点到A点的轴向距离l′=1 835 mm，如表8所示。按照上述验证E点方法得到G点径向振动位移幅值理论值与实测值的对照见表8。由表6～表8可知，径向振动位移测量点的幅值理论值与实验测试值比较相符，最大相对误差在3.0%以内，表明本文结合部径向动态特性参数识别方法是正确的、有效的，达到了较高的辨识精度。

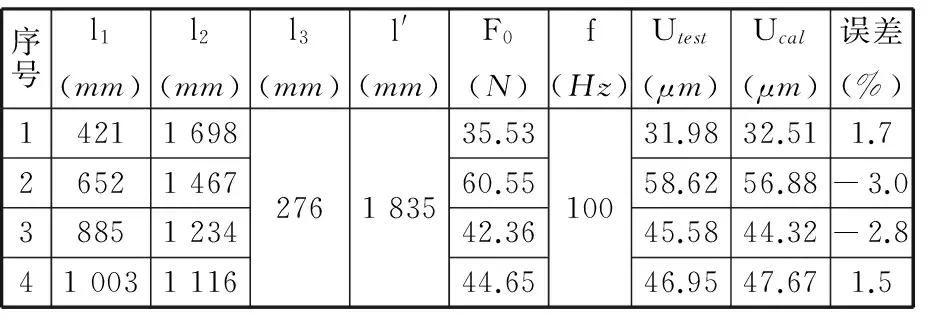
表8 激振频率为100 Hz时G点径向振动位移实测值与计算值

5 结论

(1)实验结果表明：根据本文方法辨识的结合部参数所计算的丝杠上测量点的径向振动位移与实验测试值之间的误差在3.0%以内，验证了本文方法的正确性和有效性。

(2)本文方法能在进给系统整机状态下准确辨识出其导轨副、两端轴承组及滚珠丝杠副滚动结合部的径向刚度与阻尼参数，这对指导滚珠丝杠进给系统的合理使用、提高机床加工精度，评估进给系统性能及装配精度具有重要意义。

[1] 蒋书运,祝书龙.带滚珠丝杠副的直线导轨结合部动态刚度特性[J].机械工程学报, 2010, 46(1): 92-99.

JIANG Shuyun，ZHU Shulong. Dynamic Characteristic Parameters of Linear Guideway Joint with Ball Screw [J]. Journal of Mechanical Engineering, 2010, 46(1): 92-99.

[2] IGARASHI T，TOKUNAGA Y，OOKUMA K.Studies on the Sound and Vibration of a Ball Screw: Sound Characteristics of a Ball Screw[J]. JSME International Journal ser Vibration，Control Engineering，Engineering for Industry，1988，31(4) : 732-738.

[3] 王建文.滚珠导螺杠低频噪音源之鉴别及改善研究[D].新竹: 清华大学，2005.

WANG Jianwen. Identify and Improve the Low Frequency Noise Source of Ball Screw Feed System [D]. Hsinchu: Tsing Hua University，2005.

[4] 陈勇将，汤文成，王洁璐. 滚珠丝杠副刚度影响因素及试验研究[J]. 振动与冲击，2013，32(11)： 70-74.

CHEN Yongjiang，TANG Wencheng，WANG Jielu. Influence Factors on Stiffness of a Ball Screw [J]. Journal of Vibration and Shock，2013，32(11)：70-74.

[5] 李松生，陈晓阳，张钢，等. 超高速电主轴轴承的动态支承刚度分析[J]. 机械工程学报，2006，42(11)：60-65.

LI Songsheng，CHEN Xiaoyang，ZHANG Gang，et al. Analyses of Dynamic Supporting Stiffness about Spindle Bearings at Extra High-speed in Electric Spindles [J].Chinese Journal of Mechanical Engineering，2006，42(11)：60-65.

[6] 芮红锋，胡小秋，郭丹枫. 角接触球轴承动态特性参数测试方法[J]. 振动与冲击，2013，32(8)：88-90.

RUI Hongfeng ，HU Xiaoqiu，GUO Danfeng. Measurement Method for Dynamic Characteristic Parametric Identification of Angular Contact Ball Bearings [J]. Journal of Vibration and Shock，2013，32(8)：88-90.

[7] HU Feng，WU Bo，HU Youmin. Identification of Dynamic Stiffness Matrix of Bearing Joint Region [J]. Frontiers of Mechanical Engineering in China，2009，4(3)：289-299.

[8] 毛宽民，邢满禧，李斌，等. 滚动直线导轨副可动结合部动力学建模[J]. 华中科技大学学报(自然科学版)，2016，44(7)：81-85.

MAO Kuanmin，XING Manxi，LI Bin, et al. Dynamic Modeling for Movable Joint of Rolling Linear Guide [J]. J. Huazhong Univ. of Sci. & Tech. (Natural Science Edition) ，2016，44(7)：81-85.

[9] DHUPIA J S，ULSOY A G，KATZ R. Experimental Identification of the Nonlinear Parameters of an Industrial Translational Guide for Machine Performance Evaluation[J].Journal of Vibration and Control，2008，14(5) :645-668.

[10] 叶健，何博侠，卜雄洙，等. 直线导轨进给机构动态特性参数测试方法[J]. 测试技术学报，2011，25(3)：205-210.

YE Jian，HE Boxia，BU Xiongzhu，et al. Test Method of Dynamic Characteristic Parameters of Feeding Mechanism [J]. Journal of Test and Measurement Technology，2011，25(3)：205-210.

[11] ZHANG H， ZHANG J， LIU H，et al.Dynamic Modeling and Analysis of the High-speed Ball Screw Feed System [J].Proceedings of the Institution of Mechanical Engineering， Part B：Journal of Engineering Manufacturing，2015,229(5):870-877.

[12] 吴沁，芮执元，杨建军，等. 滚珠丝杠进给系统刚度建模及仿真[J]. 现代制造工程，2010，11(26)：5-9.

WU Qin，RUI Zhiyuan，YANG Jianjun，et al. The Stiffness Modeling and Simulation of Ball Screw Feed System [J]. Modern Manufacturing Engineering，2010，11(26)：5-9.

[13] 罗亮，张为民，周敏剑，等. 滚珠丝杠进给系统动态特性集中质量建模与仿真[J]. 农业机械学报，2015，46(12)：370-377.

LUO Liang，ZHANG Weimin，ZHOU Minjian,et al. Dynamic Characteristics Modeling and Simulation of Ball Screw Feed Drive System Based on Lumped Mass Model [J]. Transactions of the Chinese Society for Agricultural Machinery，2015，46(12)：370-377.

[14] XIAO J M，ZHENG X M，WANG X H，et al.A Modified Artificial Fish-swarm Algorithm [C] //Proceedings of the World Congress on Intelligent Control and Automation(WCICA).Washington: IEEE，2006:3456-3460.

[15] WANG L G，HONG Y.A Multivalent Artificial Fish-swarm Algorithm[C]//The 7th World Congress on Intelligent Control and Automation.Washington: IEEE，2008:3161-3166.

[16] GELENBE E，SCHMAJUK N，STADDON J，et al.Autonomous Search by Robots and Animals: a Survey [J].Robotics and Autonomous Systems，1997，22(1): 23-34.

[17] 李晓磊，邵之江，钱积新.一种基于动物自治体的寻优模式: 鱼群算法[J]. 系统工程理论与实践，2002，22(11):32-38.

LI Xiaolei，SHAO Zhijiang， QIAN Jixin.An Optimizing Method Based on Autonomous Animates:Fish-swarm Algorithm[J].Systems Engineering—Theory & Practice，2002，22(11): 32-38.