基于双目视觉的工程车辆定位与行驶速度检测
2018-03-06同志学贺利乐王消为
同志学 赵 涛 贺利乐 王消为
西安建筑科技大学机电工程学院,西安,710055
0 引言
工程车辆作业时的实际行驶速度及相对于作业环境的位置信息对车辆控制至关重要,如何快速检测这些运动参数是值得研究的。传统的车速测量一般是通过检测驱动轮的转速及车轮半径而获得的,但当出现滑转时所测的速度已不是实际车速[1]。目前对实际车速的测量通常采用五轮仪测速、线圈测速、雷达测速等方法[2],但这些方法也有诸多不足,例如:五轮仪的低速性能及路面适应性较差;线圈测速位置固定,使用不灵活;雷达测速易受干扰且不适合低速测量。工程车辆的行驶速度较低,工作环境多样,滑转率较高,上述方法难以满足其实际速度测量的精度要求。近年来,视觉测量技术由于具有非接触性和被动性的优点[3]而在运动参数测量方面得到了广泛应用。目前,车载视觉测速系统一般是在车辆上安装单目视觉传感器,通过采集车辆行驶时的地面序列图像,根据序列图像的匹配进而计算出车辆的行驶速度[4],但该方法无法确定车辆相对于环境的位置。
双目立体视觉可以有效地确定物体的位置信息,因此,能通过双目序列图像同时获取工程车辆的相对位置与实际速度。本文将双目视觉系统侧向安装在工程车辆上,连续采集车辆行驶时的周围环境图像;并根据各帧左右图像的立体匹配结果,计算出环境特征点的景深,从而确定车辆相对于工作环境特征点的位置;同时对相邻两帧图像进行特征跟踪匹配,根据匹配特征点的三维坐标估算车辆的运动参数,再利用L-M (Levenberg-Marquardt)法进行优化,最终计算出车辆的行驶速度。
1 基于双目视觉的测距定位与速度估计原理
光轴平行的双目相机模型求解过程较为简单,在实际应用中甚广,因此,本文也采用此类相机。摄像机坐标系以其瞬时成像点为原点,XC轴与车辆瞬时运动方向相同,YC轴垂直于地面;ZC轴指向环境特征点。
双目视觉测距的原理就是通过图像匹配与三角测量原理计算物体在左右图像上的成像偏差,以此获取物体景深。首先对各帧双目图像进行立体匹配以获取视差,再结合双目视觉系统的标定参数从而计算出环境特征点在左摄像机坐标系下的三维坐标,其中Z坐标值就是车辆到这些环境特征点的距离,从而确定了车辆在环境中的相对位置。
基于视觉的速度估计一般都是通过序列图像的特征跟踪匹配进行的,图1为本文所用自车速度估计模型的示意图。车辆在行驶过程中可以视为刚体运动,刚体的运动参数可由旋转矩阵R和平移矢量T描述;而摄像机固定在车辆上,随车一起运动,可以认为摄像机坐标系与车体坐标系重合,则可用相邻两帧间摄像机坐标系的变换参数来描述车辆的运动参数。假设在车辆运动前后的相邻两帧图像中,对应的特征匹配点对集合Q={(iPtk、iPtk+1),i=1,2,…,N},其中,iPtk、iPtk+1分别代表在tk时刻和tk+1时刻,第i组匹配点对在左摄像机坐标系下的三维坐标,则它们有如下关系:
iPtk+1=R(iPtk)T+T
(1)
式中,R、T为相邻两帧之间左摄像机坐标系变换的正交旋转矩阵和平移矢量,表示车辆在tk+1时刻相对于tk时刻的位姿变化。
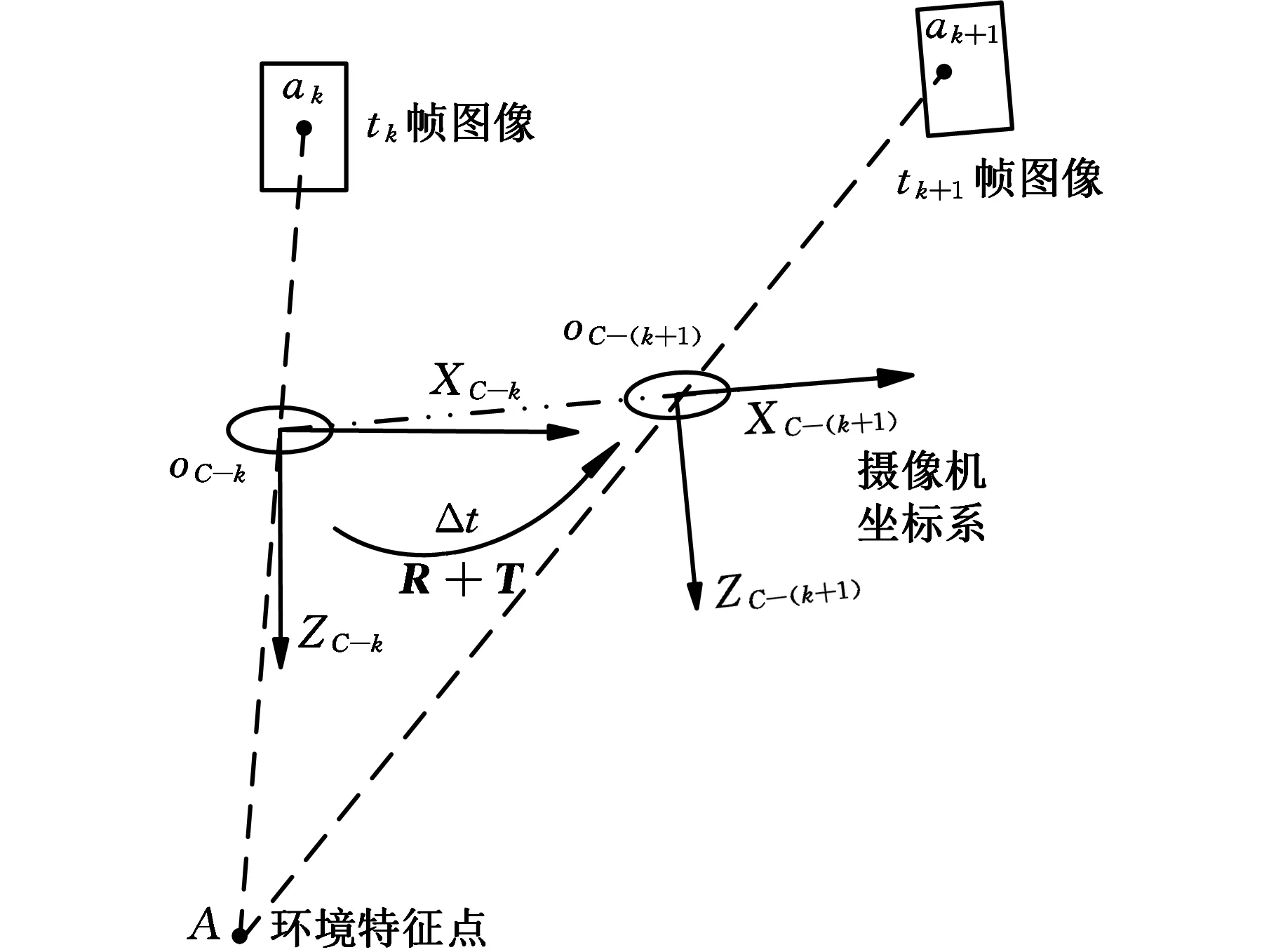
图1 车辆自车速度估计模型示意图Fig.1 Schematic diagram of ego-velocity estimation for vehicle
根据行驶路面的实际情况,车辆在相邻两帧之间的运动可以进一步视为平面刚体运动。因此,旋转矩阵R和平移矢量T可简化为
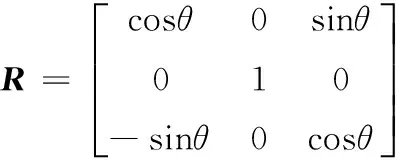
(2)
T=(tX,0,tZ)T
(3)
式中,θ为车辆的偏转角度;tX、tZ为平移分量。
求解出旋转矩阵R和平移矢量T后,就可以计算出车辆从tk时刻到tk+1时刻的平移速度v和偏转角速度ω:
v=‖T‖/Δt
(4)
ω=|θ|/Δt
(5)
由于图像采集时间间隔Δt非常小,故计算出的速度可以当作车辆的瞬时速度。根据上述原理,基于双目视觉的车辆测距定位与自车速度估计的详细流程如图2所示。

图2 基于双目视觉的车辆定位与自车速度估计方法流程图Fig.2 Flow chart of localization and ego-velocity estimation for vehicle based on binocular vision
2 立体匹配与特征跟踪匹配
在进行图像匹配之前,首先对图像进行校正、滤波等预处理。校正的目的是使图像的外极线与扫描线重合,以便立体匹配时减小搜索范围。对校正后的图像再进行高斯滤波,以去除图像中的高斯噪声。
车辆在运动过程中,摄像机采集到的图像会发生旋转、缩放、光照强度等方面的变化,而SURF(speed up robust features)算法与SIFT(scale invariant feature transform)算法一样,对图像旋转、缩放和光照强度等具有鲁棒性,且它的速度比SIFT算法快很多[5-7],所以可采用SURF算法来提取特征。
提取SURF特征后,以欧氏距离作为匹配相似性度量函数,采用最近邻/次近邻比值法,分别以左右图像为基准进行双向匹配,满足左右一致性才能判断为正确匹配点。经过极线校正后的对应特征点基本处于同一行,那么每个特征点的实际搜索范围可限制在以同一行为中心的上下3行。同时,为降低误匹配率,采用简化的RANSAC (random sample consensus)算法[8]对得到的匹配点对进行过滤。完成立体匹配后,获取视差图并对其进行滤波处理,最后结合摄像机标定参数即可计算出这些匹配特征点的三维坐标。
特征跟踪匹配的目的是建立车辆运动前后左图像特征点间的对应关系。当车辆运动到tk+1时刻获取双目图像后,完成立体匹配的同时将左图像与运动前tk时刻的左图像进行特征跟踪匹配。由于本文为估算车辆的实时速度,图像采样间隔较小,前后两帧之间有较大重合度,故可以采用前述立体匹配方法进行特征跟踪匹配。为了减少误匹配,采用以下方法。
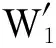
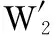
(6)
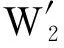
3 车辆运动参数估计
经过图像立体匹配和特征跟踪匹配之后,得到车辆运动前后N组匹配特征点对的坐标集合Q,通过这些坐标就可计算出式(1)中的正交旋转矩阵R和平移矢量T。考虑到距离车辆较远的特征点对车辆的偏转运动是敏感的,车辆小角度的偏转将使远距特征点在图像中的位置发生较大的变化;距离车辆较近的特征点对车辆的平移是敏感的,车辆的平移运动会使近距特征点的位置发生较大变化[9]。那么利用远距特征点计算旋转矩阵,近距特征点计算平移矢量,在一定程度上就降低了车辆运动估计的误差。在前后两帧图像匹配的特征点对集合Q中,选择Nf组景深(Z坐标值)较大的匹配点对构成远距点对集合Qf,Nn组景深较小的匹配点对构成近距点对集合Qn,Nf、Nn的值不能太小,否则运动参数估计误差较大,但一般也不要大于N/2,要根据实际场景选择合适的值。
3.1 运动参数初步估计
对于旋转矩阵R的求解方法有奇异值分解(SVD)法、正交分解(OD)法和单位四元数分解法[10]。其中,单位四元数分解法稳定性好,能够得到很好的数值结果,旋转矩阵R与单位四元q=[q0,q1,q2,q3]之间的关系为
R=
(7)
从Q中随机选取4组非共线的匹配点对,依据文献[11]中的Horn单位四元数法估算出旋转矩阵的初值Re,并代入式(1)求出Τe。由于误匹配点对的存在,计算出的旋转矩阵误差较大,一般采用RANSAC法进行精确求解,步骤如下:
(1)利用单位四元数法估算M={Re、Te},并将Q中剩余的匹配点对中代入式(1),设置一个误差限e,若各匹配点对的误差满足:
ei=‖iptk+1-(Re(iptk)T+Te)‖2≤e
(8)
则认为这对匹配点对为内点,否则为外点。
(2)多次重复步骤(1),并选择内点数最多的一组重新计算M。
可以看出RANSAC法的计算量较大。本文采用远距匹配点对和近距匹配点对分别估计旋转矩阵和平移矢量,在一定程度上已经降低了估计误差;再考虑到本文模型中旋转矩阵R和平移矢量T的特点:①detR接近1;②T中的第2个元素t2接近于0,且满足‖T‖≤vmaxΔt,最大车速vmax与Δt都已知。那么根据先验信息①对R进行筛选,就可以避免利用错误的R去统计正确匹配点对,减少了整体计算量。具体步骤如下。
(a)从远距点对集合Qf中随机选取4组非共线的匹配点对,利用单位四元数法估算Re,设置阈值σ,若满足σ≤detRe,则认为Re是候选旋转矩阵。
(b)多次重复步骤(a),可得到多组候选旋转矩阵Re(j)。
(c)利用候选旋转矩阵将近距点对集合Qn中的匹配点对代入式(1),每个Re(j)都会得到Nn个的平移矢量Te,根据先验信息②对这Nn个Te进行排除,得到k个满足条件的Te。则每个Re(j)对应的最佳平移矢量为
(9)
(d)将每组对应的Re(j)、Te(j)代回原匹配点对集合Q中,根据式(1)计算正确匹配点对的数目,选择正确匹配点对数目最多的一组{Re(initial),Te(initial)}作为初步估计的最终值。
3.2 运动参数优化估计
用单位四元数表示旋转矩阵R如式(7)所示,其中,q0+q1+q2+q3=1,则R共有3个独立参数(q1,q2,q3),加上平移矢量T三个参数,则运动参数的待优化量
α=[q1q2q3txtytz]T
(10)
然后利用以下目标函数求解满足其最小值的α:
(11)
令h(α)=R(iptk)T+T,则式(11)可以表示为
f(α)=(iptk+1-h(α))T·(iptk+1-h(α))
(12)
利用Levenberg-Marquardt(L-M)算法求解式(12),迭代计算过程如下[12]:
(1)以上文初步估计得到的{Re(initial),Te(initial)}作为优化初值α;

(3)∂α=(JTJ+λI)-1JTr,则αnew=α+∂α;
(4)若f(αnew) 参数λ、β、ε为经验值,应根据实际场景和精度要求选取。本文中λ、β、ε的取值分别为0.01,10,0.000 001。在获得优化后的旋转矩阵和平移矢量后,利用式(2)和式(3)就可求得θ、tX、tZ。 为了验证所提方法的有效性,进行模拟试验。图3所示为试验装置,AGV小车上安装有Bumblebee2双目视觉系统,相机分辨率为648像素×488像素,帧频为每秒48帧。试验环境为室外水泥路面,光照强度适中(多云天气);试验中小车沿“直线-圆弧-直线”路线行驶,各阶段以给定速度大小(0.4 m/s、0.2 m/s、0.4 m/s)匀速前进;摄像机每隔0.25 s采集一帧道路旁的场景双目图像。 图3 试验装置Fig.3 Test equipment 首先对采集到的各帧双目图像进行极线校正、高斯滤波处理。然后对预处理后的左右图像进行立体匹配,并根据匹配结果计算环境特征点的三维坐标。图4所示为某时刻的立体匹配结果,该时刻立体匹配后获得的部分环境特征点三维坐标见表1,其中,Z坐标值就是小车到该环境特征点的距离。 图4 某时刻立体匹配结果Fig.4 Image matching results at a certain moment 特征点编号tk时刻特征点坐标(X,Y,Z)1(22.226,-30.932,766.384)2(12.908,-25.373,683.549)3(31.918,28.246,671.893)4(11.790,12.766,769.812)5(15.595,-26.373,781.284)6(19.429,18.277,656.984) 对相邻两帧左图像进行特征跟踪匹配,并获取这些匹配特征点对的三维坐标,用以估计小车运动参数。图5所示为某相邻两帧间的特征跟踪匹配结果。 图5 某相邻两帧左图像特征跟踪匹配结果Fig.5 The results of image matching and tracking for two adjacent left frames 为了验证本文所用基于远距点和近距点的运动参数估计算法的效率和准确率,利用小车直线行驶阶段相邻两帧匹配点对的三维坐标,分别使用RANSAC法和本文方法估计旋转矩阵和平移矢量。试验所用计算机配置为AMD E-475 2.3GHz CPU和4.0GB内存;用于运动估计的匹配点对总数一致,共进行10次计算,每次重复采样100次。统计每次计算所用时间,以及X、Z方向的运动估计误差的平方和。结果如图6所示,可以看出RANSAC法用时约25 ms,本文方法用时约15 ms,相比缩短约40%;与RANSAC法相比,本文方法具有更高的精度,且误差波动较小,在一定程度上提高了算法的鲁棒性。 (a)计算用时 (b)误差图6 两种方法计算用时及误差Fig.6 Calculation time and error of two methods 计算出各时刻运动参数的预估值后,利用L-M法进行优化求解;最后根据优化值,利用式(4)和式(5)估计出小车在各时刻的平移速度和偏转角速度,并与设定的理论速度大小进行比较,结果如图7所示。可以看出本文方法具有较高的估计精度,平均误差均在6%以内。 (a)平移速度曲线 (b)偏转角速度曲线图7 车辆速度曲线Fig.7 Vehicle velocity profile 本文提出了一种基于双目视觉的车辆定位与自车速度检测方法,同步获取车辆相对于周围环境的位置与速度信息。模拟试验结果表明,该方法具有可行性,能够在一定环境条件下有效地获取运动车辆的相对位置与速度,并且根据特征点分类策略的运动参数估计方法有效地减少了计算量。今后可以进行不同环境条件下的模拟试验,进一步验证该方法的稳定性。 [1] 金守峰,胡永彪,田明锐. 基于序列图像的车载测速方法与实验[J]. 合肥工业大学学报(自然科学版),2013,36(3): 271-272. JIN Shoufeng,HU Yongbiao,TIAN Mingrui. Vehicle-borne Speed Measurement Method and Experiment Based on Image Sequences [J].Journal of Hefei University of Technology,2013,36(3): 271-272. [2] 金守峰. 基于机器视觉的工程机械行走速度测量系统研究[D]. 西安:长安大学,2015:8-13. JIN Shoufeng. A Research on Engineering Machine Speed Detection System Based on Machine Vision [D]. Xi’an:Chang’an University,2015:8-13. [3] YAMAGUCHI K, KATO T, NINOMIYA Y. Vehicle Ego-motion Estimation and Moving Object Detection Using a Monocular Camera [C]// Proceedings of the International Conference on Pattern Recognition.IEEE,2006:610-613. [4] 刘红亮,陈维义,许中胜. 基于序列图像匹配的车载自主测速方法[J]. 系统工程与电子技术,2015,37(4): 964-965. LIU Hongliang, CHEN Weiyi,XU Zhongsheng. Research on Vehicle-borne Autonomous Velocity Measurement Method Based on Sequence Image Matching [J]. Systems Engineer and Electronics,2015,37(4): 964-965. [5] 纪利娥,杨风暴,王志社,等. 基于边缘与SURF算子的SAR与可见光图像配准方法[J]. 应用光学,2013,34(5): 811-812. JI Li’e,YANG Fengbao,WANG Zhishe,et al. SAR and Visible Image Registration Method Based on Edge and SURF Algorithm [J]. Journal of Applied Optics,2013,34(5): 811-812. [6] BAY H, TUYTELAARS T, VAN GOOL L. SURF: Speeded Up Robust Features [C]//Proceedings of European Conference on Computer Vision. Graz,2006: 404-407. [7] 化春键,陈莹. 高精度尺度不变特征点匹配方法及其应用[J]. 中国机械工程,2014,25(12): 1655-1656. HUA Chunjian,CHEN Ying. Precise Scale Invariant Feature Matching and Its Application[J]. China Mechanical Engineering,2014,25(12): 1655-1656. [8] 赵烨,蒋建国,洪日昌. 基于RANSAC 的SIFT 匹配优化[J]. 光电工程,2014,41(8): 60-61. ZHAO Ye,JIANG Jianguo,HONG Richang. An Optimized SIFT Matching Based on RANSAC [J]. Opto- Electronic Engineering,2014,41(8): 60-61. [9] 尹俊,董利达,迟天阳. 基于特征点分类策略的移动机器人运动估计[J].计算机应用,2015,35(2): 590-594. YIN Jun,DONG Lida,CHI Tianyang. Mobile Robot Motion Estimation Based on Classified Feature Points [J].Journal of Computer Applications,2015,35(2): 590-594. [10] 代俣西,沈秋,王惠南,等. 双目视觉中基于对偶四元数的三维运动估计[J]. 光学技术,2015,41(2):132-135. DAI Yuxi,SHEN Qiu,WANG Huinan,et al. 3D Motion Estimation of Binocular Vision Based on Dual Quaternion [J]. Optical Technique,2015,41(2):132-135. [11] 曹凤萍,王荣本. 基于立体视觉的月球车运动估计算法[J]. 吉林大学学报(工学版),2011,41(6): 1593-1595. CAO Fengping,WANG Rongben. Stereovision Based Ego-motion Estimation Algorithm for Lunar Rover [J]. Journal of Jilin University (Engineering and Technology Edition) ,2011,41(6): 1593-1595. [12] 许允喜,蒋云良,陈方. 基于2D-3D双目运动估计的立体视觉定位算法[J].光电工程,2011,38(9): 106-107. XUN Yunxi,JIANG Yunliang,CHEN Fang. Stereo Visual Localization Algorithm Based on 2D-3D Binocular Motion Estimation [J]. Opto-Electronic Engineering,2011,38(9): 106-107.

4 试验




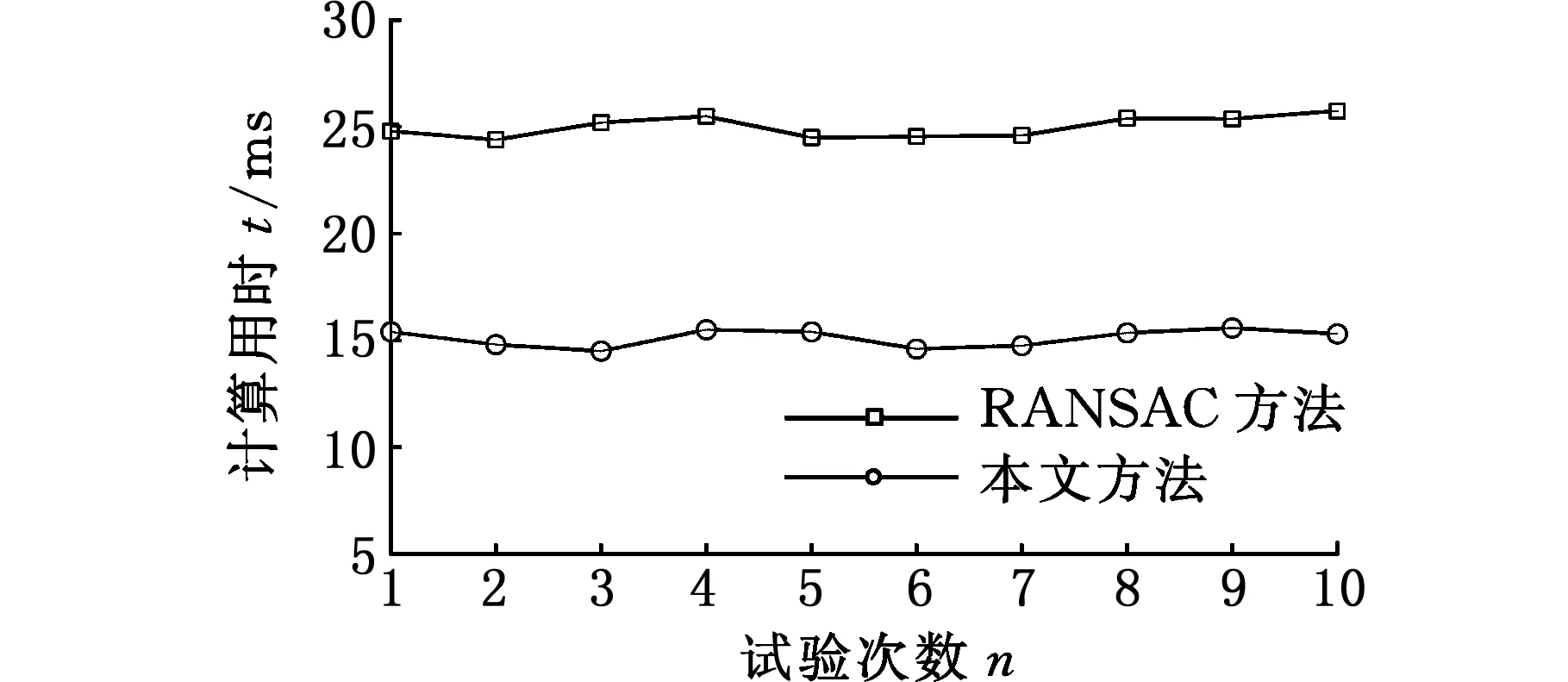


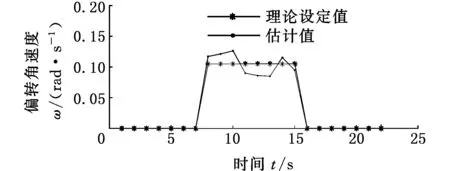
5 结论
