矩阵特征值和特征向量存在性的新证明

杨 燕 妮

(喀什大学 数学与统计学院, 新疆 喀什 844006)

众所周知,对复数域C上的有限维向量空间,矩阵或算子谱理论研究的一个基本问题是讨论其特征值和特征向量的存在性.它也是进一步讨论线性算子的谱分解和不变子空间的基础.关于矩阵的特征值和特征向量方面有着广泛的研究,如文献[1-2].

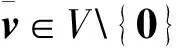
定理1的传统证明大多借助行列式理论.首先,证明λ∈C是特征值⟺特征多项式det(T-λI)=0;其次,由代数基本定理证明∃λ∈C使得det(T-λI)=0[3].特别地,对实数域R上的有限维向量空间,为证明矩阵(算子)特征值的存在性,可借助中值定理先证明“每个奇次实系数多项式均有一个实根”这一结论[4].或者利用“奇数维实向量空间上的线性算子至少有一个实特征值”的结果,通过代数方法推出任何复向量空间上的线性算子存在特征值[5].

设v∈V{0}且dimV=r.关于线性算子特征值和特征向量存在性的非行列式证明的基本思路是:首先,证明向量组v,T(v),T2(v),…,Tn(v)线性无关,即由(anTn+…+a0I)(v)=0推出a0=…=an=0.其中,a0,…,an∈C;其次,由代数基本定理, 对r∈{1,…,n}和λ1,λ2,…,λr∈C,将特征多项式改写为(T-λ1I)∘(T-λ2I)∘…∘(T-λrI)(v)=0;最后,证明对j∈{1,…,r},(T-λjI)不可逆[6-7].

值得注意的是:上面指出的证明方法都依赖于多项式根的存在性.然而,在特征值和特征向量的定义中并未涉及多项式,并且在大多数情况下,它们的数值计算也无需求多项式的根.这就表明特征值和特征向量的存在性证明可不必依赖多项式.无独有偶,在赋范代数的谱理论中已有类似证明,其基本思路是:假设函数λ∈C(T-λI)-1有定义. 然后, 通过Liouville定理、最大模原理、Weierstrass定理等导出矛盾,从而证明算子的特征值和特征向量存在[8-9].

本文给出定理1不依赖多项式和算子代数的一个非常初等的证明.之所以称其初等是因为它只用到多变量连续函数、线性映射逆的定义和几何级数的求和公式.

对给定的多项式P,Argand在证明代数基本定理[10]时,首先定义了函数z∈C|P(z)|,然后再证明该函数的最小值为0.受此启发,可对替代函数(v,λ)∈(V{0})×C→‖T(v)-λv‖/‖v‖作最小估计.因此,算子特征值和特征向量的存在性问题就转化为证明替代函数的最小值为0.下面,从推导替代函数存在最小序对入手进行证明.为便于推导,不妨赋予V任意范数.

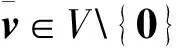
因替代函数的值域不是紧集,故需借助有限维赋范向量空间上线性算子的有界性.为此,先给出λ的一个合理估计.

引理1 设V是C上的有限维赋范向量空间.若T:V→V是线性算子,则∃C∈[0,∞)使得对∀v∈V都有‖T(v)‖≤C‖v‖;进一步,对∀v∈V和λ∈C,都有‖T(v)-λv‖≥(|λ|-C)‖v‖.

证明 第1个不等式是有限维赋范向量空间上线性算子的经典结论[8].由三角不等式可得第2个结论,即

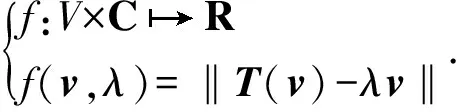
f(v,λ)>f(v0,0).

(1)

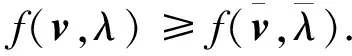
(2)

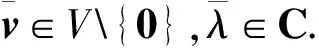
命题2表明,若最小序对不是线性算子T对应的特征值及特征向量,则线性算子T的特征值及特征向量将对应另外的最小序对.

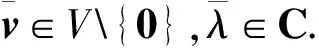
引理3 设V是C上的有限维赋范向量空间,S:V→V是线性算子,σ,ω∈C,n∈N. 若对∀j∈{1,…,n-1},ωj≠1且ωn=1,满足S可逆且对∀j∈{0,1,…,n-1},S-ωjσI也可逆,则

证明 首先,注意到

I-(σS-1)n=(Sn-σnI)∘S-n.

(3)

对n用归纳法,可以证明

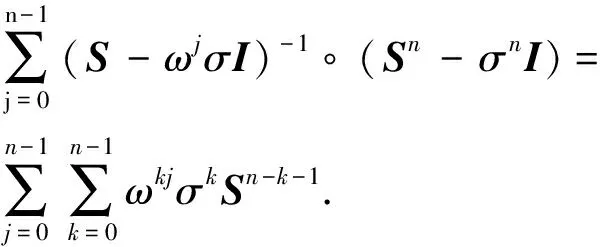
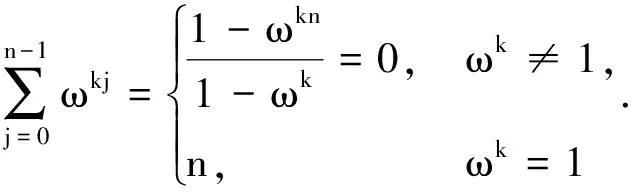
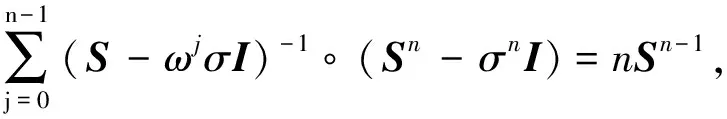
利用式(3)即可得出结论.

(4)

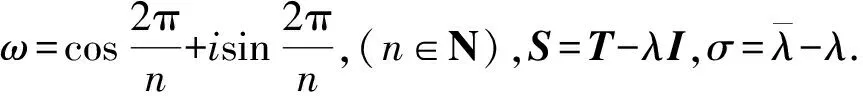
由式(4), 对j∈{1,…,n-1}有

另一方面,由式(4)又可得

因此,使用前面的不等式,可得

用n乘以式(4),可以推出

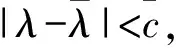
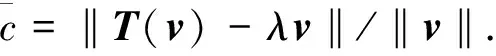
(5)

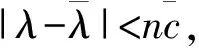
[ 1 ] 李艳艳,王东政. 严格对角占优M-矩阵最小特征值的新界[J]. 沈阳大学学报(自然科学版), 2015,27(3):255-258.

LI Y Y,WANG D Z. The new bound of the minimum eigenvalue for strictly diagonally dominantM-matrices[J]. Journal of Shenyang University (Natural Science), 2015,27(3):255-258.

[ 2 ] 曾富红,司伟建,曲志昱. 基于Hermitian矩阵的特征分解算法[J]. 沈阳大学学报(自然科学版), 2016,28(6):521-517.

ZENG F H,SI W J,QU Z Y. The eigendecomposition algorithm based on Hermitian matrix[J]. Journal of Shenyang University(Natural Science), 2016,28(6):521-517.

[ 3 ] 王萼芳,石生明. 高等代数[M]. 3版. 北京:高等教育出版社, 2003.

WANG E F,SHI S M. Advanced algebra[M]. 3rdedition. Beijing: Higher Education Press, 2003.

[ 4 ] 谢彦麟.多项式理论研究综述[M]. 哈尔滨:哈尔滨工业大学出版社, 2016.

XIE Y L. A review of the research ofpolynominal theory[M]. Harbin: The Polytechnic University of Harbin Press, 2016.

[ 5 ] 陈辉. 近世代数观点下的高等代数[M]. 杭州:浙江大学出版社, 2009.

CHEN H. Advanced algebra under the view of abstract algebra[M]. Hangzhou: Zhejiang University Press, 2009.

[ 6 ] 阿克斯勒. 线性代数应该这样学[M]. 3版. 北京:人民邮电出版社, 2016.

AXLER S. Linear algebra should be learned this way[M]. 3rdedition. Beijing: Posts and Telecommunications Press, 2016.

[ 7 ] SHELDON A. Linear algebra done right[M]. New York: Springer Verlag, 1997.

[ 8 ] 李国祯. 实分析与泛函分析引论[M]. 北京:科学出版社, 2004.

LI G Z. An introduction to real analysis and functional analysis[M]. Beijing: Science Press, 2004.

[ 9 ] SCHAFTINGEN J V. Proving the existence of eigenvalues and eigenvectors by Weierstrass's theorem[J]. American Mathematical Monthly, 2011,120(8):741-746.

[10] 陆柱家,李福安. 代数基本定理与线性代数[J]. 数学译林, 2008 (1):91-93.

(LU Z J,LI F A. Algebraic fundamental theorem and linear algebra[J]. MathematicsTranslations, 2008(1):91-93.