V形双拱独塔斜拉桥主梁无索区长度

殷任宏, 李 渊, 邬晓光

(1. 长安大学 公路学院, 陕西 西安 710064;2. 西安公路研究院, 陕西 西安 710065)

斜拉桥主梁无索区段是由弹性支撑向刚性支撑逐渐过渡的过程, 不同的无索区长度设置对结构会产生不同的影响[1-3]. 目前关于斜拉桥无索区长度的研究多集中在矮塔斜拉桥, 刘凤奎等[4]以厦门主跨80m的银湖桥为研究对象, 通过数值分析方法分析了梁端及塔根无索区长度对矮塔斜拉桥拉索索力、主梁受力的影响规律, 得到塔根无索区合理长度为主跨径的0.2～0.4倍, 边支座无索区合理长度为主跨径的0.3～0.4倍. 邹广林等[5]以佛山某(83+150+83)m三跨单索面矮塔斜拉桥工程实例为研究背景, 采用数值分析方法分析了不同的中跨无索区长度对主梁的弯矩、应力和挠度等结果的影响, 确定了斜拉桥中跨合理无索区长度与主跨径比值为0.20～0.25. 田兴等[6]以某(75+130+75)m三跨单索面矮塔斜拉桥工程实例为研究背景, 采用数值分析方法分析了单索面矮塔斜拉桥主梁无索区长度对主梁受力的影响, 确定塔根无索区长度与桥梁主跨长度的合理比值为0.12～0.16, 中跨跨中无索区长度与桥梁主跨长度的合理比值为0.14～0.20.

因为V形双拱独塔斜拉桥具有造型优美、性能优越、经济性良好等优点[7-10],近年来,国内先后修建了沈阳市浑河三好桥、延吉市新园桥、贵州荔波县官塘大桥、朝阳市新城东街大桥及西安富裕路沣河大桥5座V形双拱独塔斜拉桥,其发展优势和潜力不言而喻,相信不久后会出现在更多的城市江河之上.目前还没有关于V形双拱独塔斜拉桥主梁无索区长度的研究,其采用了索辅梁的设计理念,主梁无索区合理长度必然与其他型式的斜拉桥不同.因此本文以沣河大桥为依托,通过分析塔根、梁端无索区长度变化对斜拉索索力、主梁及拱塔内力和位移的影响规律,结合已建的5座双拱独塔斜拉桥主梁无索区长度参数统计结果,确定主梁无索区长度的合理取值范围,为类似优化结构设计提供相关依据.

1 工程概况

西安沣河大桥主桥为空间双索面的双拱独塔斜拉桥,跨径为(80+80)m,半漂浮体系.桥塔为V形拱塔,沿桥梁中心线分别向两侧倾斜25°,塔高51.466 m,其中桥面以上部分高38.718 m;拱塔采用钢箱梁,横向2.5 m,纵向2.8 m;主梁为单箱多室的扁平钢箱梁,梁高1.8 m;拉索采用8对空间密索体系,每对拉索均包含1根水平索和2根斜拉索,纵横向均对称,塔上竖向上索的距离为2.8 m,纵向拉索间距为8 m;塔根和梁端的无索区长度分别为9.45 m和6 m,如图1所示.

2 有限元分析模型

利用Midas Civil 2015软件建立双拱独塔斜拉桥空间结构计算模型,如图2所示.建模时,采用一般梁单元模拟钢箱主梁、钢拱塔,采用考虑恩斯特公式修正的等效桁架(只受拉力)单元模拟拉索,全桥模型共建367个节点,310个梁单元,48个桁架单元.采用“刚性连接”(主梁节点为主节点,拉索节点为从属节点)模拟钢箱主梁和斜拉索吊点连接,索塔与水平索的连接通过共有节点进行处理.通过改变仿真模型中的边界条件对塔梁墩不同连接方式进行模拟,采用弹性连接中的刚性连接来模拟塔梁固结和塔梁墩固结,由于对墩顶设支座,则不建立主墩单元,采用一般支承进行模拟.

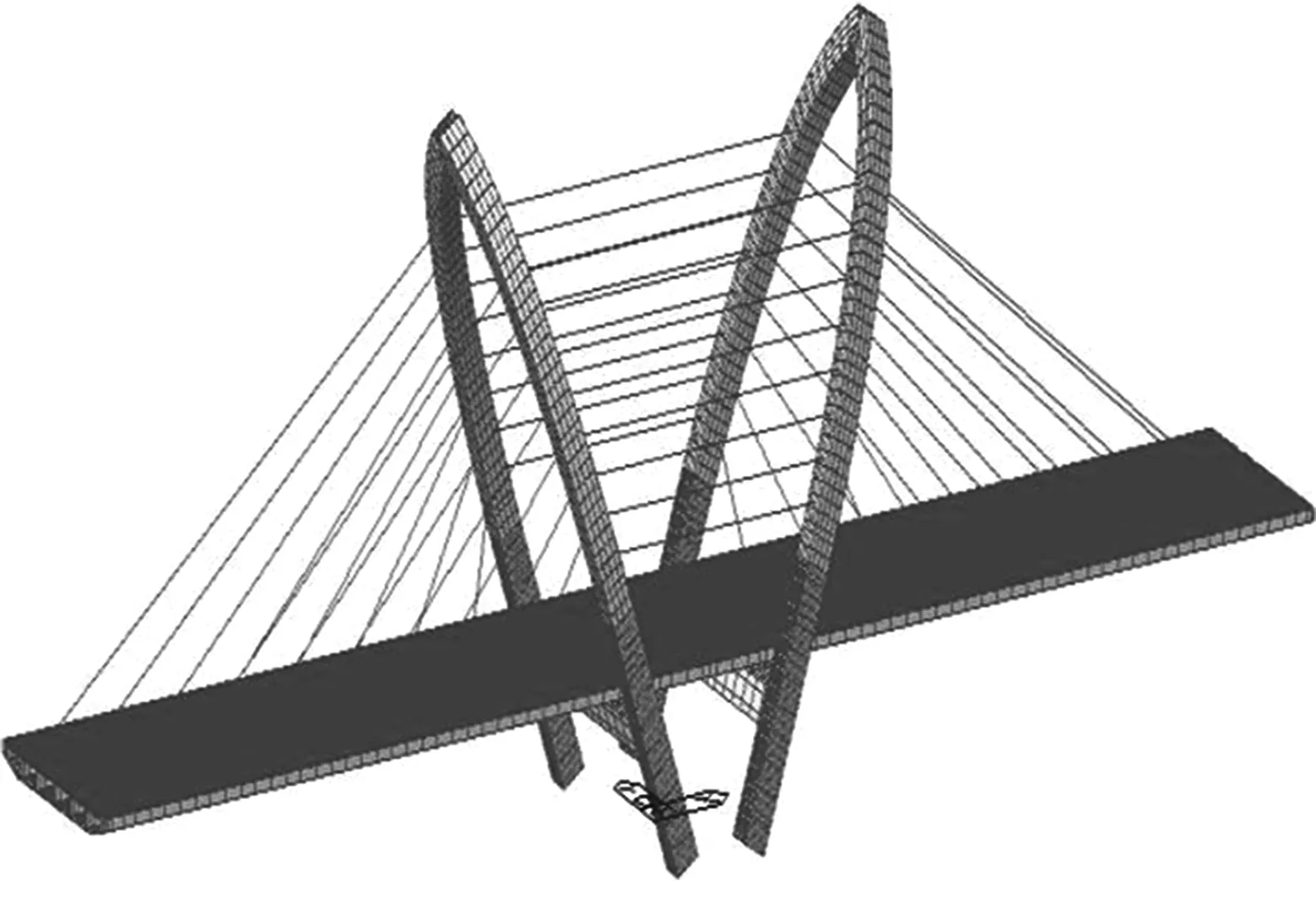
图2 沣河大桥有限元模型图Fig.2 Finite element model of Fenghe River Bridge

3 V形双拱独塔斜拉桥主梁无索区长度对结构性能的影响

为了深入研究V形双拱独塔斜拉桥主梁无索区长度对结构性能的影响,以主梁无索区长度l与主跨跨径L之比作为变量,主梁端部无索区的相对长度l1/L分别取0.05、0.1、0.15、0.20及0.25,塔根无索区的相对长度l2/L分别取0.10、0.15、0.20、0.25及0.30.

3.1 主梁无索区长度对合理成桥状态的影响

采用梁鹏等[11]提出的最小弯矩能量法优化成桥状态,得到恒载作用下不同无索区长度的成桥状态.

(1) 梁端无索区长度对合理成桥状态的影响.图3、图4为恒载作用下不同梁端无索区长度成桥状态下的索力,表1为主梁和拱塔的最大正负弯矩Mmax值.

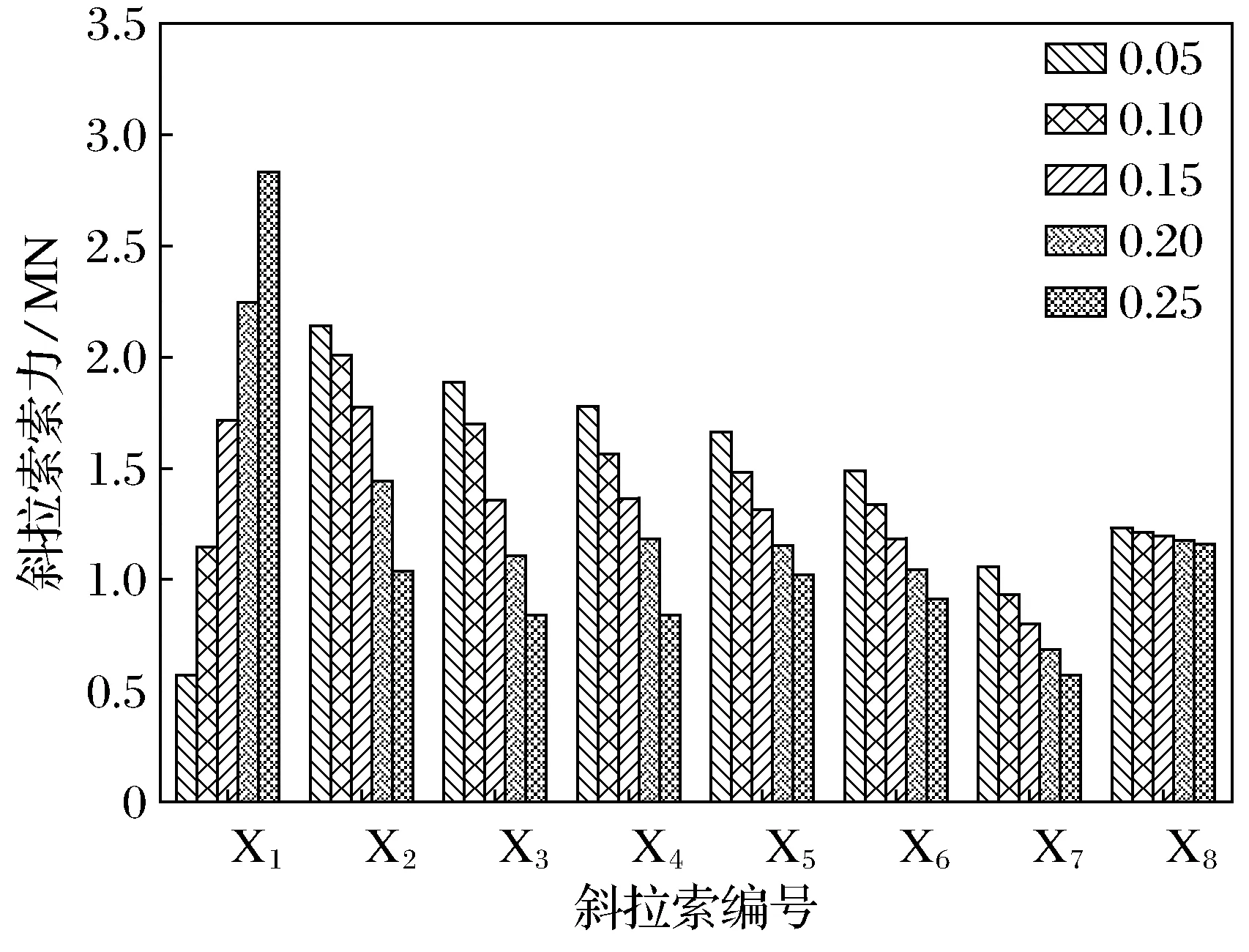
图3 不同梁端无索区长度斜拉索索力

由图3、图4可知,随着梁端无索区长度增加,最外侧斜拉索X1和水平索S1索力增加,而其他斜拉索和水平索索力呈减小趋势;梁端无索区长度对靠近梁端的斜拉索和水平索影响较大,且越靠近梁端索力所受影响越大.

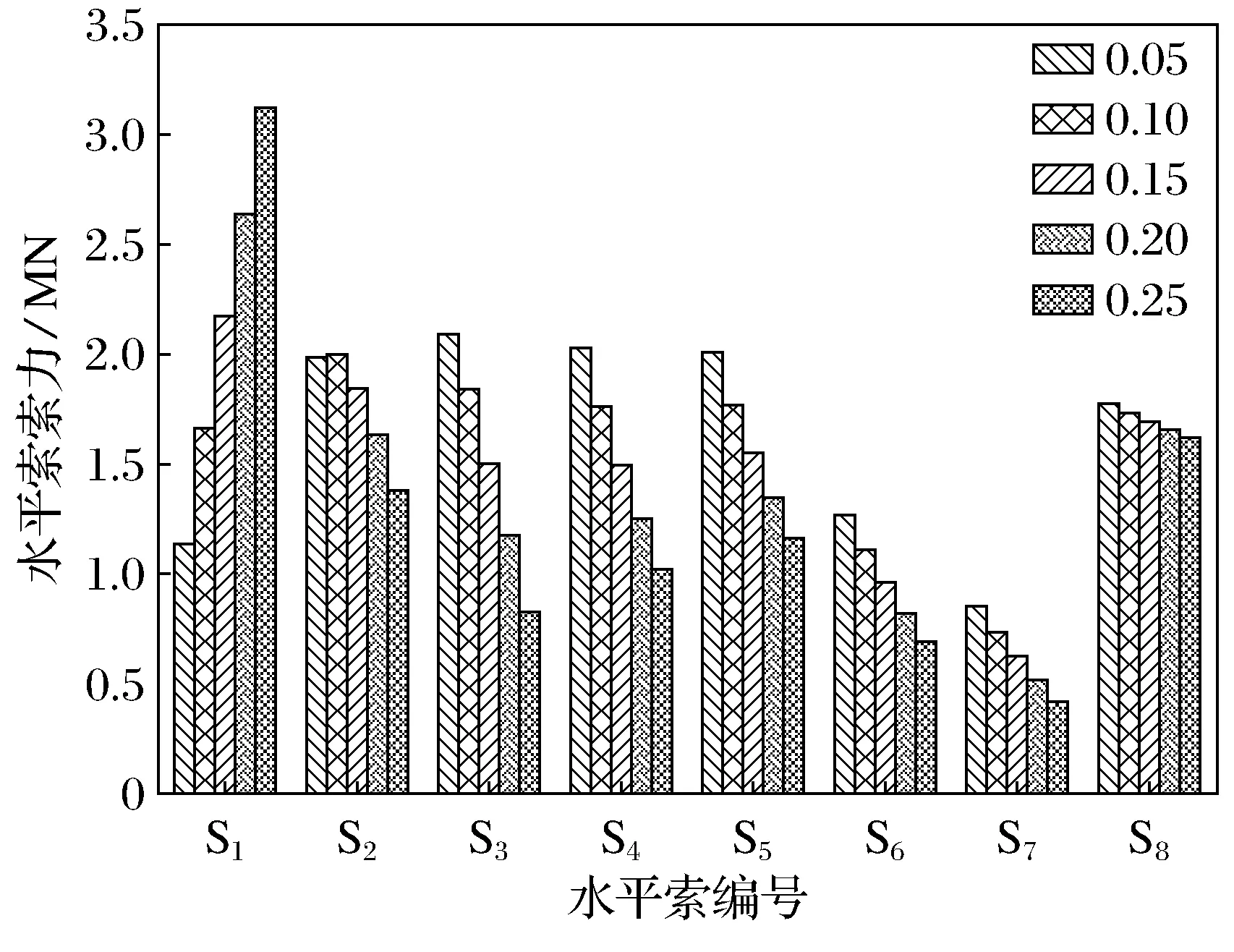
图4 不同梁端无索区长度水平索索力

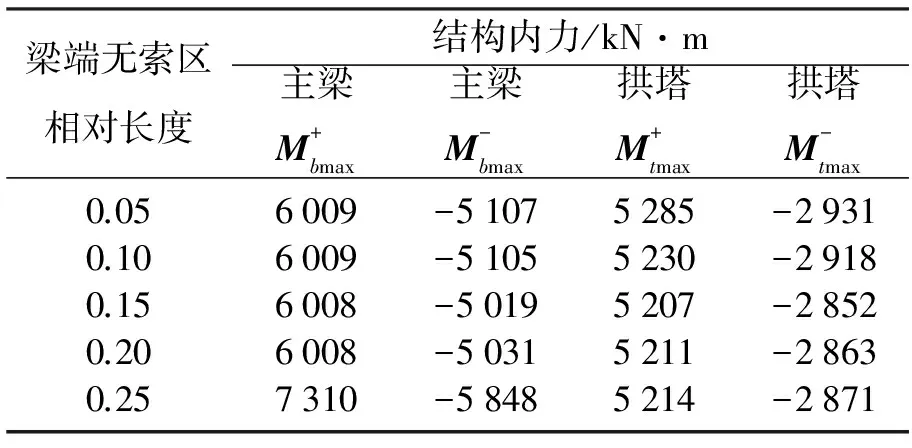
梁端无索区相对长度结构内力/kN·m主梁M+bmax主梁M-bmax拱塔M+tmax拱塔M-tmax0．056009-51075285-29310．106009-51055230-29180．156008-50195207-28520．206008-50315211-28630．257310-58485214-2871

由表1可知,随着梁端无索区长度增加,主梁和拱塔的最大正负弯矩均呈先增大后减小的趋势,且整体上变化幅度不大,但梁端无索区相对长度从0.20增加到0.25时,主梁最大正负弯矩绝对值出现较大增幅,主要原因是无索区长度过大时,梁端无索区段主梁的弯矩成为控制全桥设计的关键.

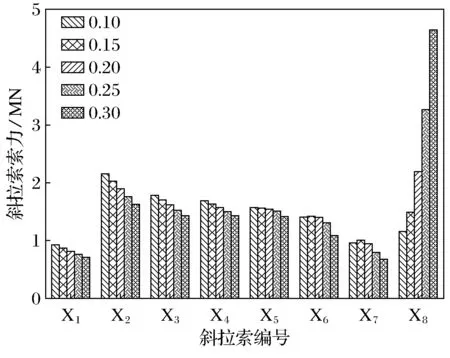
图5 不同塔根无索区长度斜拉索索力

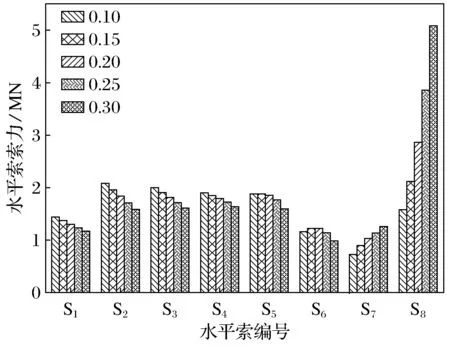
图6 不同塔根无索区长度水平索索力

(2) 塔根无索区长度对合理成桥状态的影响.图5、 图6为恒载作用下不同塔根无索区长度成桥状态下的索力值,表2为主梁和拱塔的最大正负弯矩Mmax值.

由图5、图6可知,随着塔根无索区长度增加,最内侧斜拉索X8和水平索S8索力增加,而其他斜拉索和水平索索力呈减小趋势,塔根无索区长度对靠近拱塔的斜拉索和水平索影响较大,且越靠近拱塔索力所受影响越大.

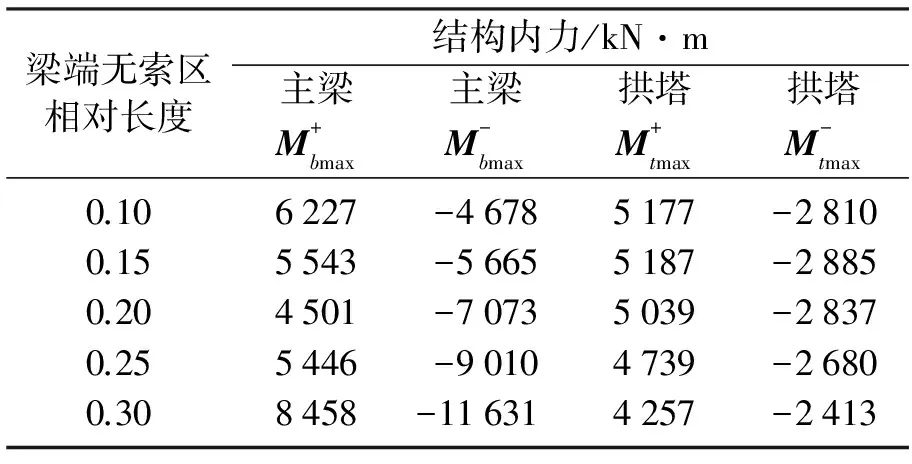
表2 不同塔根无索区长度恒载状态内力值

由表2可知,随着塔根无索区长度的增加,主梁最大正弯矩呈先减小后增大的趋势,主梁最大负弯矩呈递减趋势,拱塔正负弯矩均呈先减小后增大的趋势,且主梁和拱塔弯矩的变化幅度均较大.塔根无索区相对长度从0.25增加到0.30时,过大的无索区长度使塔根无索区段主梁的弯矩成为控制全桥设计的关键,主梁最大正负弯矩均出现较大增幅.

3.2 主梁无索区长度对活载作用效应的影响

为研究主梁梁端、塔根无索区长度对活载作用下结构内力和变形的影响规律,计算公路-Ⅰ级载荷作用下不同主梁梁端、塔根无索区长度时的结构响应,在计算时考虑了斜拉索的垂度效应,并计入恒载的初始力状态;由于主梁刚度对无索区合理长度有较大影响,主梁惯性矩Ib分别取原设计值的0.5、1.0和2.0倍.

(1) 梁端无索区对活载作用效应的影响.主梁、拱塔的内力及变形随梁端无索区长度相对值在0.05～0.25范围内的变化情况如图7所示.

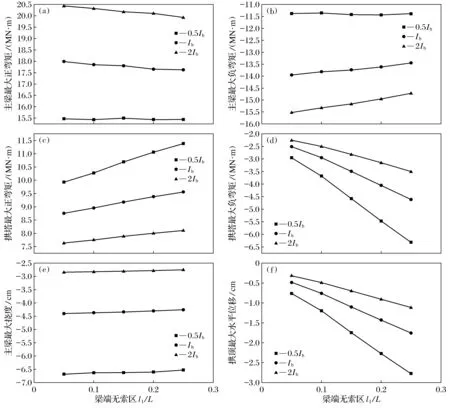
图7 主梁及拱塔最大弯矩、位移随梁端无索区长度变化关系图

由图7可知,梁端无索区长度变化对主梁最大弯矩、挠度影响较小,而对拱塔最大弯矩及变形影响较大.主梁最大正弯矩和最大负弯矩、挠度的绝对值随着梁端无索区长度的增加均表现出逐渐减小的趋势,且不同主梁刚度下最大正、负弯矩减小的幅度不同,刚度越大减小幅度越大;梁端无索区长度的增加会增大拱塔的最大正弯矩和最大负弯矩、拱顶最大水平位移的绝对值,且随着主梁刚度的增大其变化幅度减小.主要原因是无索区长度增加会使拉索倾角增大,拉索索力增大,从而拱塔弯矩及拱顶水平位移增大;随着主梁刚度的增大,拉索索力增大的幅度减小,拱塔弯矩、轴力及拱顶水平位移增大的幅度减小.

(2) 塔根无索区对活载作用效应的影响.塔根无索区相对长度值在0.1～0.3范围内变化时,主梁、拱塔的最大正负弯矩、最大挠度的变化情况如图8所示.

由图8可知,随着塔根无索区长度的增大,主梁与拱塔的最大正弯矩及变形变化不大,而最大负弯矩变化较大;主梁和拱塔的最大正弯矩、主梁最大负弯矩和挠度的绝对值整体呈现增大的趋势,且随着主梁刚度的增大变化幅度减小;而拱塔最大负弯矩、拱顶最大水平位移绝对值整体呈现减小的趋势,且随着主梁刚度增加其变化幅度减小.主要原因是双拱独塔斜拉桥主梁刚度较大,拉索仅起到辅助主梁受力的作用,而无索区长度增加会使拉索倾角减小,拉索对主梁的支承效率减小,从而主梁弯矩、挠度增大,拉索索力增大,拱塔弯矩、拱顶水平位移减小.

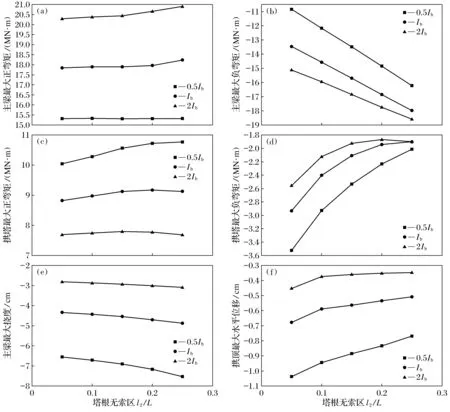
图8 主梁及拱塔最大弯矩、位移随塔根无索区长度变化关系图

4 无索区长度参数统计分析

通过对国内已建的5座双拱独塔斜拉桥主梁无索区长度参数进行整理统计,并与矮塔斜拉桥进行对比分析.

由表3可知,V形双拱独塔斜拉桥拉索在主梁上分布范围广,主梁无索区长度较短,且主梁拱塔根部无索区较梁端处无索区长度较长;V形双拱独塔斜拉桥的梁端无索区长度l1与主跨跨径L之比为0.07～0.09,与矮塔斜拉桥的0.20～0.35相比较小;塔根无索区长度l2与主跨跨径L之比为0.10～0.15,与矮塔斜拉桥的0.15～0.20接近.

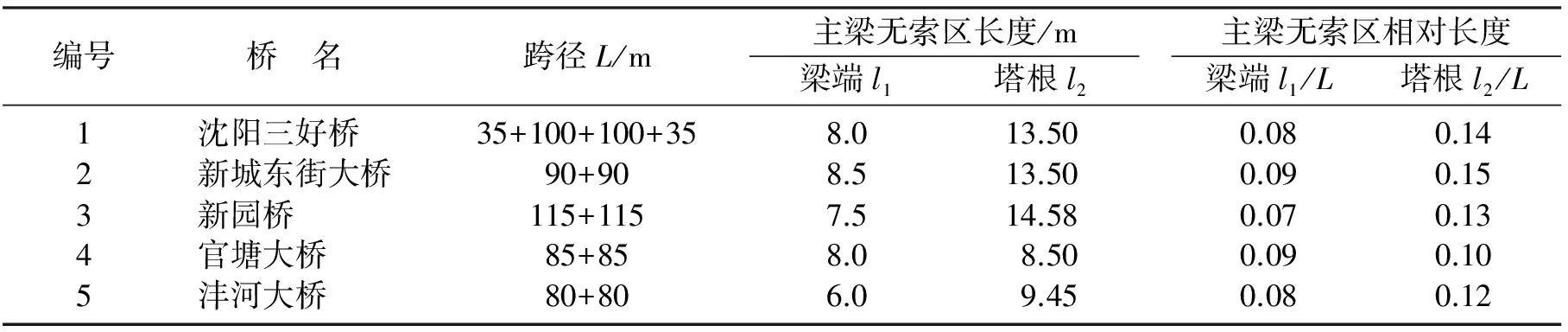
表3 国内V形双拱独塔斜拉桥主梁无索区长度参数统计表Table 3 Statistical table of non-lengths of cable-stayed bridge with V-shaped double arch single pylon

5 结 论

(1) V形双拱独塔斜拉桥主梁、塔根无索区长度对结构受力的影响程度较大,而梁端无索区对结构受力影响程度较小.因此,在设计时可通过调整塔根无索区长度来改善结构的受力性能.

(2) 梁端无索区长度l1与主跨跨径L之比宜为0.05～0.10;塔根无索区长度l2与主跨跨径L之比宜为0.10～0.15.

[ 1 ] 陈德伟,范立础,张权. 独塔斜拉桥的总体布置和参数研究[J]. 土木工程学报, 1999,32(3):34-40.

CHEND W,FAN L C,ZHANG Q. Studies on parameters and general arrangement of single tower cable-stayed bridges[J]. China Civil Engineering Journal, 1999,32(3):34-40.

[ 2 ] 雒建哲. 拱塔斜拉桥设计参数及几何非线性分析[D]. 长沙:中南大学, 2011.

LUO J Z. Analysis on design parameters and geometric non-linear of arch cable-stayed bridge[D]. Changsha: Central South University, 2011.

[ 3 ] 李东潇. 索辅体系斜拉桥合理成桥状态及设计参数研究[D]. 长春:吉林大学, 2013.

LI D X. Research on reasonably completed state and design parameters of partially cable-stayed bridge[D]. Changchun: Jilin University, 2013.

[ 4 ] 刘凤奎,蔺鹏臻,陈权,等. 银湖矮塔斜拉桥无索区长度分析[J]. 铁道标准设计, 2004(5):11-13.

LIU F K,LIN P Z,CHEN Q,et al. An analysis of the length of non-cable area of the low pylon cable-stayed bridge over Yinhu Lake[J]. Railway Standard Design, 2004(5):11-13.

[ 5 ] 邹广林,李新平,曾永雄. 斜拉桥下中跨无索区合理长度分析[J]. 低温建筑技术, 2016,38(12):69-71.

ZOU G L,Li X P,ZENG Y X. Analysis of thereasonable length of span without cable in cable-stayed bridge[J]. Low Temperature Architecture Technology, 2016,38(12):69-71.

[ 6 ] 田兴,完海鹰. 单索面矮塔斜拉桥主梁无索区长度对主梁受力的影响[J]. 工程与建设, 2015(4):471-474.

TIAN X,WAN H Y. The influence of the length of the main beam without the cable length on the stress of the main beam[J]. Engineering and Construction, 2015,04:471-474+515.

[ 7 ] 郭廷泰,韩晓虎,安平和,等. 基于FAHP法钢箱梁斜拉桥主梁施工方案比选[J]. 沈阳大学学报(自然科学版), 2016,28(3):237-243.

GUO Ti T,HAN X H,AN Pi H,HE Pan. Construction planning decision of steel box girder bridge based on FAHP method[J]. Journal of Shenyang University(Natural Science), 2016,28(3):237-243.

[ 8 ] 于德安,檀永刚,张哲. 钢斜拉桥的稳定性评估[J]. 沈阳大学学报(自然科学版), 2014,26(5):408-412.

YU D A,Tan Y G,ZHANG Z. Stability evaluation of steel cable-stayed bridge[J]. Journal of Shenyang University(Natural Science), 2014,26(5):408-412.

[ 9 ] 于玲,钟右鹏,包龙生,等. 沈阳市三好桥钢拱塔拉索施工关键技术研究[J]. 沈阳建筑大学学报(自然科学版), 2010,26(2):292-295.

YU L,ZHONG Y P,BAO L S,et al. The study on Shenyang Sanhao Bridge steel arch cable-stayed construction key technologies[J]. Journal of Shenyang Jianzhu University(Natural Sciences), 2010,26(2):292-295.

[10] 苟祖宽. 荔波官塘大桥双斜钢拱塔无支架原位拼装方案研究[J]. 贵州大学学报(自然版), 2014,31(3):116-120.

GOU Z K. Scheme study of non-bracket original position assembly of steel box arch pylons of Libo Guantang Bridge[J]. Journal of Guizhou University(Natural Science), 2014,31(3):116-120.

[11] 梁鹏,肖汝诚,张雪松. 斜拉桥索力优化实用方法[J]. 同济大学学报(自然科学版), 2003,31(11):1270-1274.

LIANG P,XIAO R C,ZHANG X S. Practical method of optimization of cable tensions for cable-stayed bridge[J]. Journal of Tongji University(Natural Sciences), 2003,31(11):1270-1274.