宽幅装配式连续T梁桥载荷横向分布系数计算方法适用性

李院军, 刘 洋, 郑 鹏, 黄 成

(1. 长安大学 公路学院, 陕西 西安 710064;2. 贵州交通规划勘察设计研究院股份有限公司, 贵州 贵阳 550000)

随着车流量的日益增多,为保证出行的快捷顺畅,宽桥在桥梁建设中使用日趋广泛,尤其是宽幅装配式连续 T 梁桥,以其施工便捷、质量高的特点在桥梁选形中脱颖而出[1-2].

在装配式连续T梁桥的设计中,载荷横向分布系数的计算是一个重要的步骤.目前主要针对窄桥进行载荷横向分布系数的研究,针对宽幅装配式连续梁桥的研究较少[3].彭泽友[4]通过有限元梁格法分析了5片装配式T梁,并与手算载荷横向分布系数计算结果进行了比较,建议采用空间计算方法复核手算方法;杨凤莲等[5]采用梁格法分析了由3～4 片小箱梁装配而成的广珠城际铁路桥梁,建议对用查表法得到的中梁结果进行修正;杨年芳[6]基于正交异性板法原理,从理论上推导了载荷作用下的宽桥横向分布表达式;赵涛[7]建立正交简支空心板宽桥和简支 T 梁宽幅桥的实体模型,对比分析通过铰接板梁法和有限元法计算得到的载荷横向分布影响线竖标值,验证建模的合理性;王仕实等[8]基于梁格理论建立简支梁桥空间梁格有限元计算分析模型,并通过与实际桥梁结构静载试验的挠度、应力等结果对比,验证了方法的正确性.

可见,大部分的研究主要是针对简支装配式窄桥,研究结果的适用范围有限,且计算载荷横向分布系数一般使用铰接板法或G-M法,由于方法较少,使得对比方法有局限性[9].多数对宽桥横向分布系数现有方法的修正研究,只是来源于单纯的数据分析,缺乏理论推导[10-11].

本文针对宽幅装配式连续T梁在载荷作用下跨中载荷横向分布系数进行研究,先把连续T梁桥简化为简支梁桥,进而用修正偏心压力法、铰接板法和G-M法计算跨中载荷横向分布系数,然后以有限元模型计算的结果作为标准进行对照,分析装配式连续T型宽桥跨中载荷横向分布系数计算方法的准确性和适用性,以寻求一定范围内的大宽跨比载荷横向分布最优计算方法及载荷横向分布具体规律.

1 分析对象和方法

1.1 分析对象

本文以4×20 m的装配式连续T梁桥为研究对象,其主梁宽度2.5 m,高度1.5 m,抗弯惯性矩为0.238 m4,抗扭惯性矩为0.039 m4.通过增加梁的片数以实现梁桥宽跨比的变化,选取0.75、1.00、1.25和1.50的4种宽跨比进行对比分析,主梁片数分别为6、8、10和12片.图1为6片主梁截面示意图.

图1 6片主梁的装配式T梁桥截面图Fig.1 The assembly type T-beam bridge section diagram of six beams

1.2 分析方法

目前对于装配式简支梁桥的载荷横向分布系数计算方法一般有杠杆原理法、修正偏心压力法、铰接板梁法、刚接板梁法、G-M法和有限元法等.其中杠杆原理法大多数用来计算支点处载荷横向分布系数;修正偏心压力法一般适用于窄桥,但对于宽跨比是多少没有明确规定;刚性横梁法把桥梁视作由主梁和横梁组成的梁格体系,作用在1片梁的载荷通过横隔梁传递到其他梁上,同时主梁又对横梁起弹性支承作用;G-M法把桥梁结构看作一个纵横交错的体系,按杆件系统的空间结构求解,同时结构也可以简化成一个矩形的薄板,从而作为弹性薄板理论进行分析[1].但对于连续梁桥,这些方法不能直接沿用.一般对肋梁式连续梁桥的载荷横向分布是通过将连续体系比拟简化为简支体系来分析.其主要的简化方法有等代简支梁法、等挠度跨径换算法、弹性支撑连续梁法和反弯点分割的静定梁法.本文采用等代简支梁法.

使用Midas Civil建模进行有限元分析,采用梁单元,有限元模型见图2.计算载荷横向分布系数的过程为:分别在各梁跨中施加1MN集中载荷,然后读取相应梁的跨中挠度值,与各梁跨中挠度值相比,得到各片梁的横向分布影响线,并在影响线上进行最不利加载,最后可求得载荷横向分布系数[12].

图2装配式T粱桥有限元模型图
Fig.2 Finite element model of assembly T-beam bridge

由文献[13]可知,对于连续桥可以换算为跨径相同的等挠曲刚度简支板来分析.只要换算出等代简支板的等代抗弯和等代抗扭刚度,就能用等待简支板来等效替代对应的实际连续板求出载荷横向分布系数.由于T梁沿纵向变化较小,故对于简化计算暂不计抗扭刚度换算.

4跨连续梁桥按“等代简支板”用式(1)求得抗弯刚度.

(1)

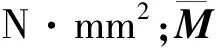
等代刚度计算公式为

(2)

式中:EIh为换算刚度,N·mm2;L为计算跨径.

具体的换算系数见表1.

表1 弯矩刚度换算Table 1 Bending moment stiffness conversion

2 载荷横向分布系数的计算

2.1 边跨载荷横向分布系数计算

分别在宽跨比0.75、1.00、1.25和1.50下,用刚接梁法、偏心压力法、G-M法和有限元法进行计算分析,并以有限元法为基准进行比较,分析出不同宽跨比下载荷横向分布系数最优算法.载荷横向分布系数计算结果见表2和图3.

根据图3和表2可知,在4个大宽跨比下,对于连续T梁边跨用修正偏心压力法计算时,从边梁到中梁误差越来越大,其最大误差值达到-21%,计算结果明显不符实际;用刚接梁法计算时,既有正误差,也有负误差,有时边梁误差大,有时中梁误差大,但计算结果误差都在±4%以内;G-M法计算时,整体计算结果都较为稳定,其计算结果误差在±3%以内,符合工程±5%的允许误差值.对于边跨整体计算精度由大到小排序为:G-M法、刚接梁法、修正偏心压力法.

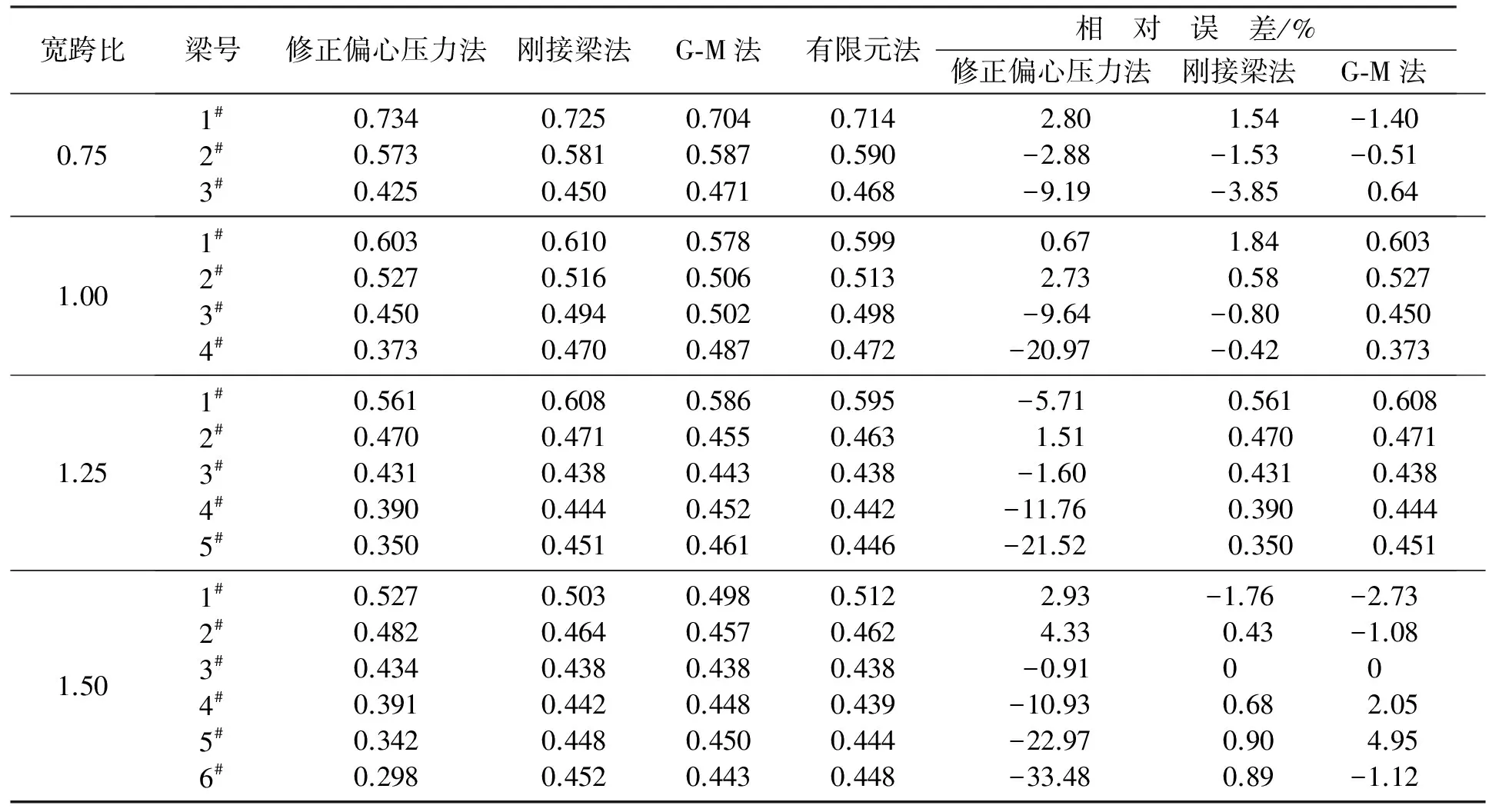
表2 各宽跨比载荷横向分布系数对比Table 2 Comparison of transverse distribution coefficients of different widths

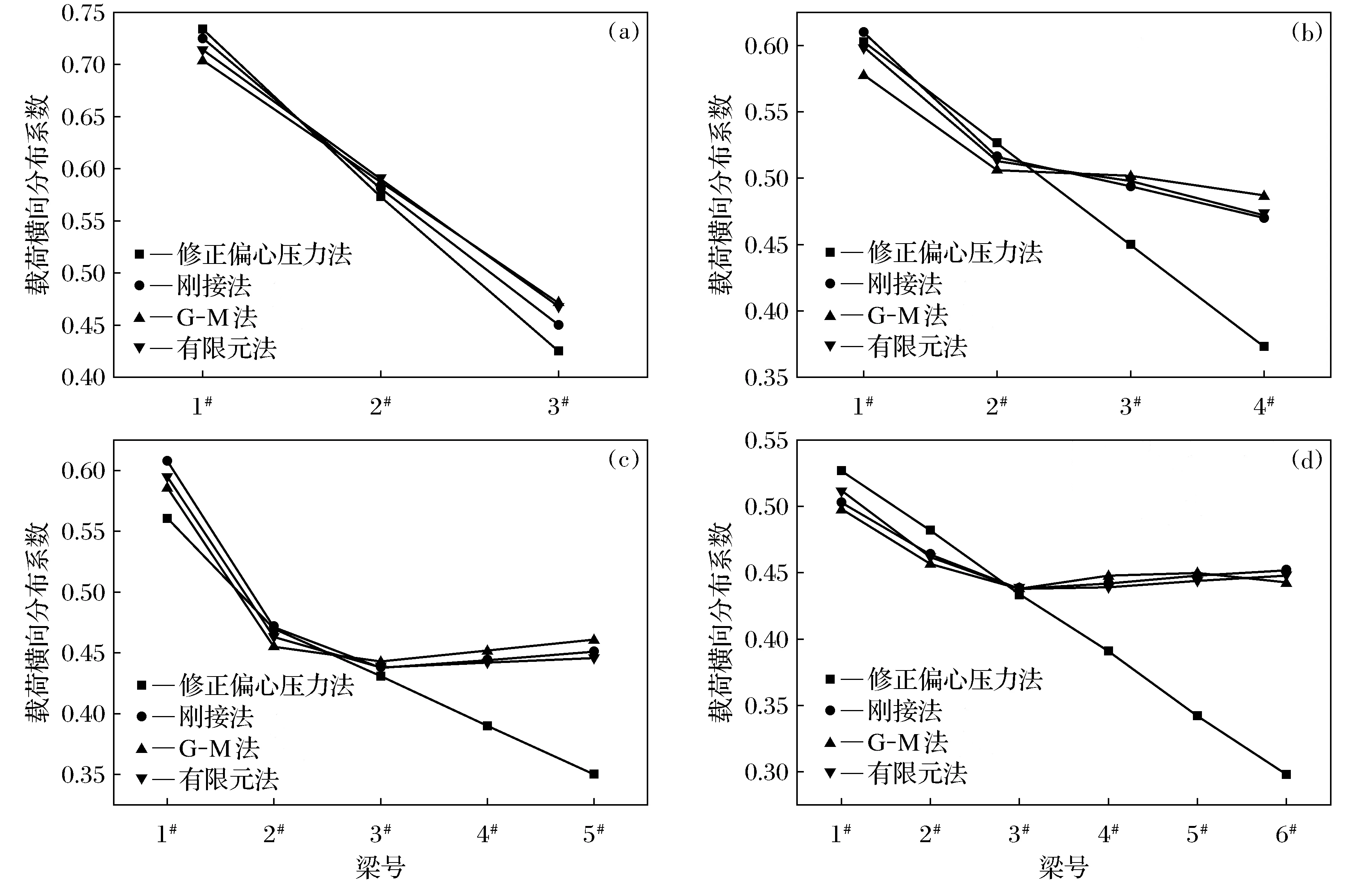
图3 4个宽跨比下载荷横向分布系数对比图Fig.3 Comparison of transverse distribution coefficients of four broad span ratios(a)—宽跨比0.75; (b)—宽跨比1.00; (c)—宽跨比1.25; (d)—宽跨比1.50.

刚接梁法计算载荷横向分布系数的前提是假定竖向载荷作用下接合处只传递竖向剪力和赘余弯矩,且用半波正弦载荷来分析跨中横向分布.随着宽跨比的增大,梁的片数增多,与有限元计算结果相比,结构的横向连接刚度减弱,且对结构实际挠曲和扭转变形考虑不足,导致边梁误差值大,中梁误差较小,但其误差值都在±5%以内,符合工程的要求.

使用修正偏心压力法计算载荷横向分布系数的前提是假设横梁无限刚度,即横梁只发生刚体位移.但随着梁的片数增多,横梁的弯曲刚度相对于主梁变小,使得横梁在横向不能再假设成无限刚度.故对于宽桥使用修正偏心压力法计算载荷横向分布系数时计算结果会有较大的误差.

为了能够精确地反映结构的实际问题,G-M法把结构简化为一块矩形的平板作为弹性薄板,按古典弹性理论来进行分析.故随着宽跨比的增大,G-M 法也能够适用,且计算结果较为稳定.

2.2 单片梁载荷横向分布系数计算

为得出单片梁随着宽跨比增大,其载荷横向分布系数的变化规律,整理计算数据结果,单独提取出边梁(1#梁)和中梁(2#梁)载荷横向分布系数计算结果进行对比分析.边、中梁载荷横向分布系数计算结果对比见表3和图4.

通过表3和图4,以及对比4种计算方法计算载荷横向分布系数的结果,可知边梁载荷横向分布系数最大,中梁最小.对于边梁,随着宽跨比的增大,其载荷横向分布系数逐渐递减;中梁随着宽跨比的增大,其载荷横向分布系数先是急剧递减,当宽跨比到达1.25时,载荷横向分布系数趋于平稳或微增长.

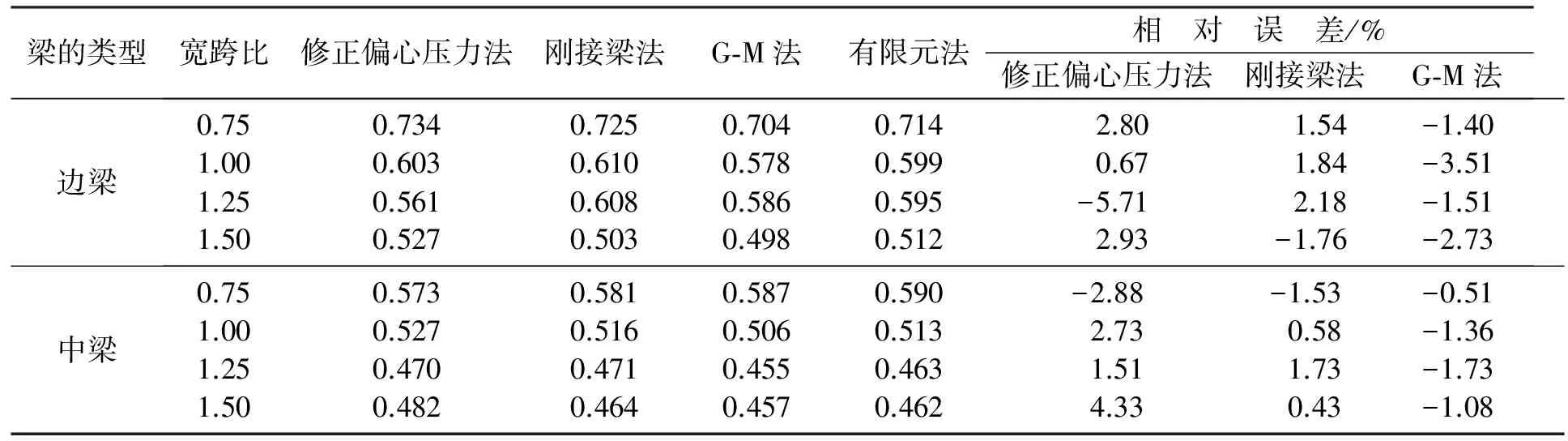
表3 边、中梁载荷横向分布系数对比Table 3 Comparison of lateral distribution coefficient of beam and middle beam

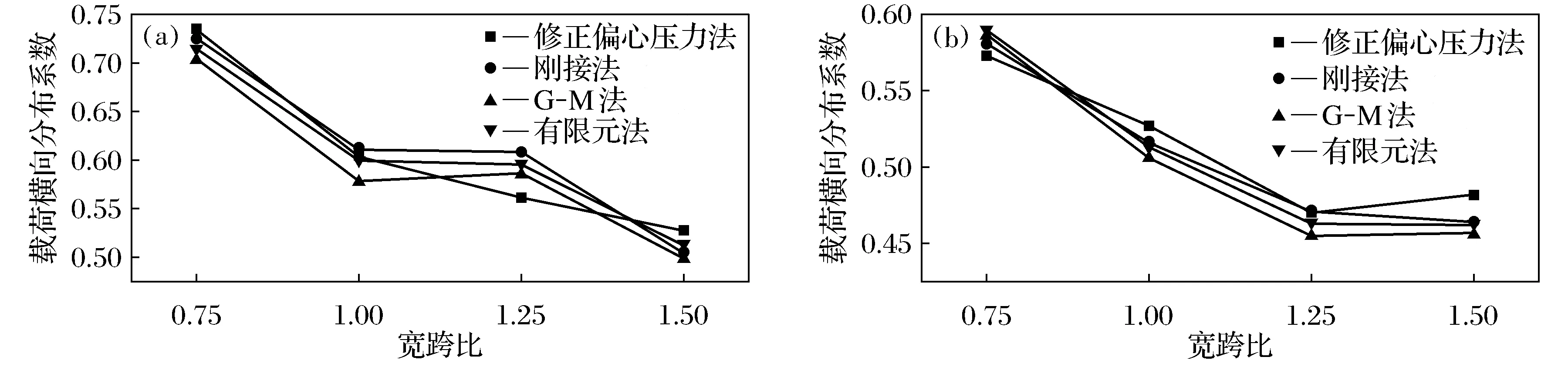
图4 边、中梁载荷横向分布系数对比图Fig.4 Comparison of lateral distribution coefficient of beam and middle beam(a)—边梁; (b)—中梁.

随着宽跨比的增大,梁的片数增加.虽然桥面布置的车辆载荷增加,但梁片数的增加所产生的效果远大于车辆载荷增大产生的效果.故会出现随着宽跨比的增大,边梁和中梁的跨中载荷横向分布系数变小,同时因为边梁的传递范围小于中梁的传递范围,边梁的载荷横向分布系数大于中梁.但当宽跨比大于1.25时,各片梁的载荷横向分布系数都趋于平稳,此时车辆载荷的传递范围有限,当到达了一定的宽度后,载荷就传递不过去了.

通过计算装配式连续T梁桥边跨和中跨的载荷横向分布系数,可知边跨各片梁的载荷横向分布系数与中跨各片梁的载荷横向分布系数相差很小,故本文只列出边跨数据.

3 结 论

(1) 对于装配式宽幅预应力混凝土连续T梁桥,计算跨中载荷横向分布系数时,刚接梁法准确性高,且随着宽跨比的增大,其计算精度整体较高,故对于宽幅装配式连续T梁桥跨中载荷横向分布系数的计算适合用刚接梁法.

(2) 在大宽跨比下, G-M法计算载荷横向分布系数结果相对较稳定,但在其计算载荷横向分布系数的过程烦琐,且较为耗时,故在设计时不推荐.修正偏心压力法计算宽桥载荷横向分布系数,由于具有明显缺陷,不予采用.

(3) 随着宽跨比的增大,各片梁的载荷横向分布系数都在递减,其中,边梁的递减程度大于中梁.当中梁宽跨比到达1.25时,载荷横向分布系数趋于平稳或微增长。

[ 1 ] 苏佩,钱若霖,邬晓光,等. 装配式简支T梁宽桥横向分布[J]. 沈阳大学学报(自然科学版), 2017,29(3):229-232.

SU P,QIAN R L,WU X G,et al. The horizontal distribution of the assembly type of simple T-beam width bridge[J]. Journal of ShenyangUniversity (Natural Science), 2017,29(3):229-232.

[ 2 ] 邬晓光,贺攀,李艺林,等. 连续刚构桥跨中横隔板设计参数[J]. 沈阳大学学报(自然科学版), 2017,29(3):223-228.

WU X G,HE P,LI Y L,et al. Design parameters of continuous rigid frame bridge span[J]. Journal of Shenyang University (Natural Science), 2017,29(3):223-228.

[ 3 ] 张永强. 大宽跨比连续T梁桥荷载横向分布系数试验研究[J]. 公路交通技术, 2015(4):75-79.

ZHANG Y Q. Experimental research on lateral distribution factors of load on continuous T-beam bridges at large and wide span ratio[J]. Highway Transportation Technology, 2015(4):75-79.

[ 4 ] 彭泽友. 装配式T梁荷载横向分布分析[J]. 公路, 2008(3):68-71.

PENG Z Y. Analysis of load transverse distribution of fabricated T-beam[J]. Highway, 2008(3):68-71.

[ 5 ] 杨凤莲,罗世东,苏竹松,等. 广珠城际简支多片箱梁桥内力横向分布研究[J]. 铁道标准设计, 2005(11):113-115.

YANG F L,LUO S D,SU Z S,et al. Research on the internal force transverse distribution of the simply-supported multiple box-girder bridge In Guangzhou-Zhuhai inter-city transportation[J]. Railway Standard Design, 2005(11):113-115.

[ 6 ] 杨年芳. 宽桥横向分布系数的精确快速计算方法[J]. 湖南交通科技, 2011,37(2):85-88.

YANG N F. Accurate and fast calculation method for lateral load distribution coefficient of wide bridge[J]. Hunan Communication Science and Technology, 2011,37(2):85-88.

[ 7 ] 赵涛. 简支宽桥分析[D]. 西安:长安大学, 2015.

ZHAO T. Analysis of the beam width bridge[D]. Xi’an: Chang’'an University, 2015.

[ 8 ] 王仕实,孙卓,蔡卡宏,等. 基于梁格法在用简支梁桥荷载横向分布应用研究[J]. 广州大学学报(自然科学版), 2012,11(5):56-60.

WANGS S,SUN Z,CAI K H,et al. Research on lateral load distribution of simple supported beam bridge based on grillage method[J]. Journal of Guangzhou University (Natural Science Edition), 2012,11(5):56-60.

[ 9 ] 钱寅泉,周正茂,王素娟,等. 装配式小箱梁桥荷载横向分布数值分析与试验[J]. 公路交通科技, 2012,29(1):86-90.

QIAN Y Q,ZHOU Z M,WANG S J,et al. Numerical and experiment of lateral load distribution of fabricated small box girder bridge[J]. Journal of Highway and Transportation Research and Development, 2012,29(1)86-90.

[10] 刘华,叶见曙,俞博,等. 桥梁荷载横向分布系数计算方法[J]. 交通运输工程学报, 2009(1):62-66.

LIU H,YE J S,YU B,et al. Calculation method of horizontal distribution coefficient of bridge load[J]. Journal of Transportation Engineering, 2009,9(1):62-66.

[11] 陈强,孟阳君,周先雁. 大宽跨比桥梁横向分布系数的快速计算方法[J]. 重庆交通大学学报(自然科学版), 2011,30(6):1287-1289.

CHEN Q,MEN Y J,ZHOU X Y. Rapid calculation method of horizontal distribution coefficient of large-width and span bridges[J]. Journal of Chongqing Jiaotong University (Natural Science), 2011,30(6):1287-1289,1334.

[12] 汤柯平. 宽幅预应力混凝土T梁桥荷载横向分布研究[D]. 重庆:重庆交通大学, 2016.

Tang K P. Lateral distribution of the beam bridge load of broad prestressed concrete[D]. Chongqing: Chongqing Jiaotong University, 2016.

[13] 李国豪,石洞. 公路桥梁荷载横向分布计算[M]. 2版. 北京:人民交通出版社, 1990.

LI G H,SHI D. Calculation of lateral distribution of highway bridge load[M]. 2nd edition. Beijing: People’s Transport Press, 1987.