基于加速因子不变原则的加速度计可靠性分析

盖炳良，滕克难，王浩伟，韩建立，李高春

（海军航空大学，烟台 264001）

加速度计是测量载体加速度的机电产品，广泛应用于各类军用和民用惯导系统中，是惯导系统的关键部件。在其工作或长期贮存中，因标度参数等关键性能参数的退化而导致产品失效[1]。随着生产工艺提升，加速度计产品可靠性不断提高，使得传统可靠性分析方法耗时耗费，因而基于加速退化数据的可靠性分析方法得到广泛研究和应用。

Wiener过程能够对非单调性的加速退化数据进行建模，适合加速度计产品的退化建模[1-2]。在Wiener退化建模中，考虑到产品制造工艺、工作环境等个体差异的客观存在，基于随机影响的Wiener退化模型得到深入研究。正常工作应力下，Peng[3]提出将Wiener模型的漂移参数μ考虑为服从正态分布的随机变量以体现个体差异，而扩散参数σ相同。此后，Bian[4]、Si[5]、Liao[6]、Li[7]、Tang[8]等都采用了该模型。之后，Peng[9]、Wang[10]、Pan[11]提出了考虑偏态正态分布等更一般性的模型。为便于描述，将该类模型记为RD模型，将不考虑个体差异的Wiener模型记为SM模型。RDV模型（即Wiener模型）的漂移参数μ和扩散参数σ都是随机变量，如Wang[12]采用w=σ-2Gam(a,b)、μwN（1,ew）模型，徐廷学[13]、蔡忠义[14]则采用w=σ-2Gam（a,b）、μwN（h,ew）模型，其中a、b、e、h都是待定参数。目前，尚未见单独考虑Wiener模型中扩散参数σ是随机变量的具体应用，可将其记为RV模型。

加速应力作用下，SM 模型中在确定应力与参数关系时主观性较大，有不同的假定。Padgett[15]、Liao[16]、Lim[17]、Sung[18]、Hu[19]等都假定漂移参数μ与加速应力相关，而扩散参数σ与加速应力无关。针对假定参数与加速应力的关系过于主观性，王浩伟[20]、Wang[21]等采用加速因子不变原则，推导得到μ、σ与加速应力都相关，且在Sk、Sh任意两个应力作用下应满足如下约束关系

加速应力作用下，考虑个体差异的模型处理方式目前有两类：① Tang[22]、Chen[23]、Cai[24]等在SM模型基础上，通过假定漂移参数μ的Arrhenius加速模型中某个参数是服从正态分布的随机变量来体现个体差异；② Sun[25]在RD模型基础上，应用加速因子不变原则，将μ、σ的加速模型引入RD模型。

综上，在加速退化数据可靠性分析中，目前大多数研究都是基于SM模型。为使模型更具适应性而考虑个体差异的模型，多数通过随机加速模型体现个体差异，而随机加速模型中随机变量是假定确定的，具有主观性；而Sun[25]以RD模型为基础，同时引入加速模型，然而其考虑的加速模型是以SM模型为基础推导得到的结论，不能全面体现出加速应力作用下RD模型参数与加速应力的约束关系。另外，在确定模型时，现有的文献大多都只选择一种模型，在参数估计后按照Wiener过程的统计特性对模型进行适用性检验，这能确定该模型是否适用，但不能解决所用模型是否相对最优。

基于以上分析，本文采用加速因子不变原则，推导得到RD、RV、RDV三类模型参数与加速应力的约束关系，并采用QQ图、DIC值、后验样本箱线图等方法进行模型综合择优选择。

1 考虑随机影响的Wiener过程

SM模型：X(t)=μΛ(t)+σB(Λ(t))，X(0)=0，Λ(t)为时间函数，Λ(0)=0，μ为漂移参数，σ为扩散参数，B(⋅)为标准Brown运动函数。平稳独立增量ΔX(t)服从正态分布：

ΔX(t)～N(μΔΛ(t),σ2ΔΛ(t))，

ΔX(t)=X(t+Δt)-X(t),ΔΛ(t)=Λ(t+Δt)-Λ(t)。

设失效阈值为D，X(t)首次到达D的时间为T=inf{tX(t)≥D}，则T服从Inverse Guassian分布[2]，可靠度函数为

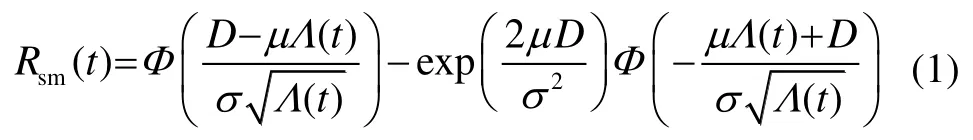
RD模型：假设μ服从分布μN(μμ,μσ)，由全概率公式可得无条件密度函数frd(X(t))，由文献[22]可得可靠度函数Rrd(t)如下：

RV模型：假设ϖ服从分布ϖ=σ-2Ga(a,b)，其中ϖ=1σ2，则：

式中，F(2a)是自由度为2a的t分布累积分布函数。

RDV模型：假设μ、ϖ服从共轭先验分布ϖ=σ-2Ga(a,b),μ ϖN(h,eϖ),其中a、b、h、e是超参数，则可推导得到：

2 加速退化建模

2.1 加速因子不变原则

任意两个应力水平Sk、Sh下的累积失效函数Fk(Λk)、Fh(Λh)，当Fk(Λk)=Fh(Λh)时，定义Sk相当于Sh的加速因子AFk,h为AFk,h=ΛhΛk。加速因子不变原则指出AFk,h是一个只有Sk、Sh所决定的常数，而与Λk、Λh时间变化无关。当Λ是时间函数时，有：

即

2.2 确定加速应力与参数关系

SM模型：文献[26]推导得到如下关系式：

在温度应力T作用下，μ（T）=e xp（γ1-γ2T），σ（T）=e xp（γ3-0.5γ2T），γ1、γ2、γ3都是未知参数，Wiener SM的加速退化模型为：

RD模型：将式(3)代入式(9)，可得：

为确保AFRD是不随时间变化的常数，则需满足：

整理可得：

RV模型和RDV模型推导过程类似，限于篇幅，给出结论如下：

2.3 建立相关参数的加速模型

以温度T为加速应力，采用Arrhenius加速模型描述参数与应力的变化关系。

RD模型：温度应力下参数可表示为

σ=

其中，γRD(1)、是待定参数。

RV模型：温度应力下参数可表示为：

由式(12)可得：γRV(2)=γRV(4)。将加速模型代入式(6)，RV模型可靠度函数如下：

RDV模型：温度应力下参数可表示为

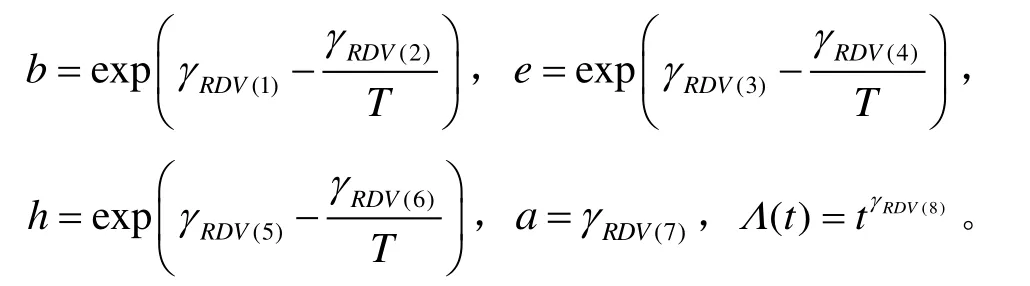
由式(13)可得：γRDV(2)=γRDV(4)=γRDV(6)。将加速模型代入式(8)，RDV模型可靠度函数为

3 参数估计和模型选择

通过 OpenBUGS软件采用马尔科夫-蒙特卡洛（MCMC）抽样方法实现参数估计，该方法首先确定参数先验分布，无可靠先验信息，则可选择较大区间均匀分布等无信息先验，然后采用 MCMC方法求后验参数估计值。OpenBUGS软件求解主要包括先验分布表达、似然函数表达，以及退化数据表达和初始值的设定。图1所示是RV模型求解中先验分布表达和似然函数表达的实现。

图1 参数估计OpenBUGS实现Fig.1 Parameter estimation by OpenBUGS

基于数据拟合的随机过程建模的模型选择：①首先模型验证。Wiener过程 ΔX(t)N(μΔΛ(t),σ2ΔΛ(t))，即通过 Kstest命令验证样本是否服从标准正态分布。分位数图（QQ图）是对样本分位数和标准正态分位数的比较，因而也可通过 QQ图更直观地判断模型对数据的拟合情况；②箱线图分析。参数的后验样本箱线图能显示参数的均值、中位数等分布特征。在模型通过统计特性验证的基础上，通过比较所有样本的参数箱线图，可以很直观判断μ、σ等参数在不同样本中是趋于相同还是具有明显的差异；③偏差信息基准（DIC）值分析。DIC值定义为是似然函数，pD是估计参数数目，即DIC是模型期望偏差与表示模型复杂度的估计参数数目之和。DIC值越小表示模型拟合越好，模型选择时可以对多个适用模型通过DIC值进行择优选择。

4 实例验证

为了对某型宝石轴承支撑摆式加速度计进行可靠性分析，文献[1-2]都对恒定应力加速退化试验数据进行了分析，该试验以温度为加速应力，选取18个样品，分成3组，每个加速应力下样本量为6，加速应力分别为T1=338.16K，T2=348.16K，T3=358.16K 。性能退化量为一次项标度因数相对于初始值的偏差值，失效阈值D=0.006，退化数据详见文献[1]。

对加速退化数据分别采用4类Wiener模型建模，参数估计值如表1所示。

表1 参数估计值Tab.1 Parameter estimation values

由Wiener过程的统计特性检验表明，RV模型各样本都接受标准正态分布，而SM模型第8个样本，RD模型第8、12、17个样本，RDV模型第6、12、13、14、16、17、18个样本都不接受标准正态分布。图2所示是4类模型的QQ图，通过QQ图可较直观反映出各模型对数据的拟合情况，RV和RDV模型拟合较好。SM、RD、RV、RDV 模型的 DIC值分别是-2702.6、-2767.7、-2817.1、-2803.5，也表明RV模型拟合较好。

图2 QQ图Fig.2 Quantile-quantile plot

图3所示是RV模型参数σ后验样本箱线图，可发现18个样本σ有较明显的个体差异。

图3 σ后验样本箱线图Fig.3 Box plots of posterior densities of σ

综上分析，可确定4类模型中RV模型拟合更好。

RV模型中参数应满足式(12)约束关系，而在3个温度应力下可形成如下 3个点：理论上3点应在直线上。参数估计时由后验样本计算可得[μT1,μT2,μT3] =[4.315× 10-13, 1.501× 10-12, 4.966× 10-12]，[bT1,bT2,bT3]=[3.94×10-16, 1.384× 10-15, 4.625× 10-15]，即(3.479, 3.513)、(3.3085, 3.3418)、(11.509, 11.739)这三个点（如图4所示）与直线距离偏差小，验证了约束关系成立。

图4 参数变化规律验证Fig.4 Validation of change rule of model parameters

将表1中RV模型参数估计值，代入式(17)可推得正常应力T=293.16K 时的可靠度函数：

可靠度曲线如图5所示，同时比较了文献[2]结果。采用文献[2]方法，即采用SM模型的可靠性分析结果过于乐观，会造成较大的偏差。按照RV模型可求得该型加速度计平均贮存寿命为184560 h，可靠贮存寿命（可靠度值为0.9）为158221 h。

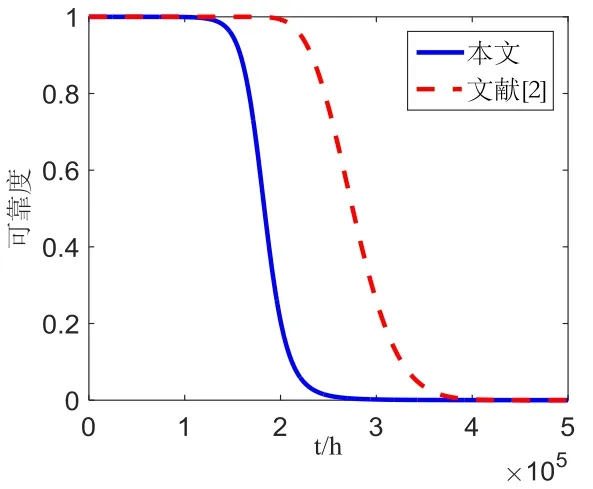
图5 可靠度曲线Fig.5 Reliability curves

5 结 论

本文以加速度计加速退化数据为对象，提出了一种基于加速因子不变原则的加速退化数据可靠性分析方法，考虑了三类随机影响模型，并采用多种方法综合选择相对最优模型。主要结论为：

①加速因子不变原则是确定退化模型参数变化规律，进而正确建立加速退化模型的有效方法。

②RD模型中漂移参数的超参数μμ、μσ以及扩散参数σ和加速应力相关，并且在任两个应力下满足约束关系RV模型中漂移参数μ以及扩散参数的超参数b和加速应力相关，并且在任两个应力下满足约束关系μk/μh=bk/bh；RDV模型中超参数b、e、h与加速应力相关，并且在任意两个应力下满足约束关系hk/hh=ekeh=bk/bh。

③考虑个体差异的加速退化模型，具有更好的适应性；基于QQ图、DIC值、箱线图综合选择模型的方法，能确定相对最优模型，为提高建模精度提供了有益参考。