基于状态相关黎卡提方程的非线性协同制导律

郭志强，周绍磊，于运治，李晓宝

（1. 海军航空大学，烟台 264001；2. 海军潜艇学院，青岛 266199）

多个拦截弹通过信息共享[1-2]、功能互补[3]的群体优势可以实现拦截能力的提高和任务范围的拓宽。但在应对多弹协同制导问题时，经典制导律如比例导引等在拦截机动目标时往往难以取得理想效果，而最优制导律由于要对目标的机动规律进行假设也导致其实用性被大大限制。微分对策制导律由于对目标信息的依赖性小且适用于机动目标的拦截而引起了相关学者的重视和研究。这类制导方法将拦截弹和目标视作正在进行博弈的双方，分别得出所有对策参与者的最优策略[4-6]，无需对目标的机动规律做任何形式的假设，可将目标机动对制导性能产生的影响降到最小。

目前关于协同拦截问题的研究，包括文献[4-6]，大多是在小角度偏差假设的基础上，将系统模型线性化之后进行制导律的设计。但是现实中的系统其本质上是非线性的，当小角度偏差的假设不能满足或者目标在其当前速度下具有很强的机动能力时，则需考虑借助其它方法来解决非线性的制导问题。

基于状态相关黎卡提方程（State-dependent Riccati-Equation,SDRE）的方法是求解非线性系统反馈控制律的一种有效方法，具有很好的实时性和灵活性。文献[6-7]均指出，当小角度偏差假设不成立时可采用基于SDRE的方法解决制导律设计问题，但二者都未给出推导过程。文献[8]首次基于SDRE方法和微分对策理论对带有角度约束的一对一追逃问题进行了研究。文献[9-10]进一步对一对一的拦截问题进行了研究，并利用SDRE方法分别推导得出了不带角度约束和带角度约束的非线性追逃对策制导律。

上述文献[4-10]均未对非线性的协同对策问题展开讨论，目前也尚未检索到采用SDRE方法对协同微分对策制导律展开研究的文献。基于此种现状，本文考虑在末制导阶段拦截弹与目标不满足初始小角度偏差假设的情况下，在微分对策理论的基础上结合SDRE方法，将难以求解的最优化问题转化为方便求解的次优问题，提出了一种非线性的协同制导律。该制导律具有解析形式，可在线应用且不依赖于剩余时间，避免了剩余时间的估计精度不足对制导律性能造成的影响。

1 协同微分对策的SDRE

为简单计，本文考虑两枚拦截弹M1和M2（追踪者）拦截单个机动目标T（逃逸者）的工况。该追逃对策（Pursuit-Evasion Strategy）问题的状态方程可写为

式中，x∈n为系统状态向量；u=［uu］T，u∈n1121和u∈n2分别为拦截弹M1和M2的控制向量；2v∈nv为目标T的控制向量；t0为系统初始时间。

拦截弹和目标的控制向量满足边界条件：

本文所讨论的拦截过程属于有限时间的范畴，但文献[11]的结果表明，在无限时间条件下推导得出的制导律依然适用。故选择性能指标泛函如下：

如果f(x)∈C1，且有f(0)=0，则系统状态方程(1)可写成状态相关系数形式：

为使该问题可解，系统需满足可控性和可观性。下面在讨论该对策问题的解之前先给出鞍点策略的定义。

定义1 如果对策双方采取的策略u*和v*存在且满足

则称(u*,v*)为该对策问题的鞍点策略（Saddle Point Strategy,SPS）。

本文研究的微分对策问题本质上是一种双边优化问题，是对策双方（两枚拦截弹作为一方而目标作为另一方）之间的一种动态博弈过程，目的是求得双方的最优机动策略（鞍点），假如某一方不按其最优策略进行机动，则它将因此而受损，同时另一方因此而获益，这种对策又称二人零和微分对策。由于求解微分对策问题的鞍点策略要涉及到哈密顿-雅克比-贝尔曼-艾萨克斯（Hamilton-Jacobi-Bellman-Isaacs,HJBI）偏微分方程的求解，而求此类问题解析解的过程往往是十分复杂的，甚至是不可能的。此时可以考虑将系统状态方程表达成如式(3)所示的形式，利用SDRE方法使难以求解的最优问题转化为方便求解的次优问题。下面对求解非线性对策问题的SDRE方法进行讨论。

如果上述微分对策问题的状态相关黎卡提方程

存在唯一的正定对称解P(x)∈n×n，则拦截弹和目标基于SDRE的控制策略可分别写成状态相关的形式：

引理1[10]对于一般的多变量系统，式(6)(7)给出的SDRE控制满足：

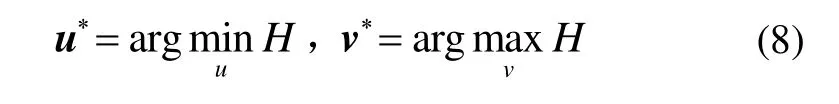
式中，H为系统的哈密顿函数。

引理2[10]对于多变量系统，在渐近稳定条件下，若A(x)、B(x)、C(x)、P(x)、Q(x)、R1(x)、R2(x)及其梯度在原点的Ω邻域内有界，则当x趋近于0时，基于SDRE的非线性控制满足如下伴随方程：

式中，λ为伴随状态。

引理3[10]假设在原点的Ω邻域内，∀x∈Ω，则：

1）A(.)∈C1，且｛A(x),B(x)｝、｛A(x),C(x)｝满足可控性，｛Q12(x),A(x)｝满足可观性；

2）对于给定ρ，式(5)存在唯一对称正定解P(x)，则当v=0或v=v*=ρ-2CT(x)P(x)x时，由式(6)可得系统的局部渐近稳定闭环解。

引理4[12]若状态相关系数具有可控性和可观性，则式(6)所示控制使得平衡点全局渐近稳定的充分条件是对于任意x，下列关系式成立：

2 协同微分对策制导问题

2.1 运动学建模与制导原理

假设弹目相对运动可在两个正交平面内解耦，双方的二维相对运动关系如图1所示。图1中：XI-OI-YI表示笛卡尔惯性坐标系，Mi表示第i(i=1,2)个拦截弹，T表示目标；V、a、γ分别表示速度、侧向加速度和航向角，下标i和T分别对应于拦截弹Mi和目标；ri表示拦截弹Mi与目标T之间的距离；φi表示拦截弹Mi与目标T之间的视线角。

图1 对策双方的平面相对运动关系Fig.1 Planar engagement geometry of the players

极坐标下拦截弹与目标之间的运动方程为

式(11)中，Vci表示弹目接近速度。式(13)中，aj为拦截弹和目标的加速度，假设双方自动驾驶仪均具有理想动态特性，则有a1=u1，a2=u2，aT=v。

将拦截弹的视线角速度表示为θi，即

对式(14)求导则有：

定义 2 从当前时刻t起，拦截弹和目标均不再施加任何控制，以当前状态运行至命中时刻tf时的脱靶量称为零控脱靶量，它与视线角速度的关系为[10]

从式(16)可以看出，拦截弹为了命中目标，可采取控制使视线角速度趋近于零且使弹目相对速度Vci＜0从而达到拦截目的，而对于目标而言则要尽可能使视线角速度增大以摆脱拦截。

2.2 状态相关系数矩阵

本文暂不考虑其它约束条件，以碰撞拦截为目的，选取视线角速度x=[θ1θ2]T作为对策问题的状态变量，则系统状态方程可写成如式(3)所示的状态相关系数形式，其中，

为了后面讨论方便，将A(x)、B(x)、C(x)中的元素分别记为

根据引理 3，｛A(x),B(x)｝、｛A(x),C(x)｝应满足可控性，其可控性矩阵为

根据系统可控性秩判据，在弹目接近速度Vc1、Vc2和弹目距离r1、r2均不为零的条件下，系数矩阵应满足

令

式中，q1>0、q2>0分别为状态变量θ1和θ2的加权系数。根据引理3，矩阵对{Q12(x),A(x)}应满足可观性，其可观性矩阵为

由系统可观的秩判据易知式(27)满足可观性要求。

2.3 SDRE解法的协同制导律

由式(6)可知，欲求基于SDRE的反馈控制律，需先求出黎卡提方程式(5)的解P(x)。假设R1(x)、R2(x)均为单位阵，下面基于SDRE的舒尔解法求解P(x)。

系统的哈密顿矩阵为

式中，F(x)=BBT-ρ-2CCT，A(x)、B(x)、C(x)分别如式(17)～(19)所示。对称阵F(x)的元素分别为

则可求得哈密顿矩阵H的特征值为

式中，

系统的SDRE存在对称正定解P(x)的条件是哈密顿矩阵在虚轴上无特征值，这就需要选取合适的权值q1、q2使得下面的关系成立：

将哈密顿矩阵H的两个负特征值和对应的特征向量组成的新矩阵V：

根据舒尔方法将矩阵V分割成两个方阵：

可得对称矩阵P(x)：

式中，

由于P为正定阵，则权值q1、q2和系数ρ的选取还应使下面的关系成立：

根据式(6)(7)，对策双方解析形式的制导律为

对于本文所研究的二对一追逃对策问题，由于目标需要综合考虑两枚拦截弹的状态信息（即视线角速度θi）来寻求自身的最优逃逸策略（使两个弹目视线角速度最大的策略），而两枚拦截弹又要根据各自相对于目标的视线角速度分别寻求自身的最优追踪策略（使各自的弹目视线角速度最小的策略），在这一过程中，两枚拦截弹的控制量通过目标的控制量产生耦合，因此所求得的两枚拦截弹的制导策略式(43)(44)也具有耦合形式。从式(43)等号右边第二项和式(44)等号右边第一项可以看到，拦截弹一方面追求自身视线角速度趋近于零，同时也对另一枚拦截弹的视线角速度产生影响，以期达到与目标完全相反的目的，体现了一种显式的协同关系。

注释1由于采用SDRE方法的微分对策制导律不需讨论剩余时间的估计问题，但作为协同制导问题，需要对整个对策过程的结束时间做出定义。为了下节仿真的方便，本文将对策的结束时间规定为目标被其中一枚拦截弹首先命中的时间，即

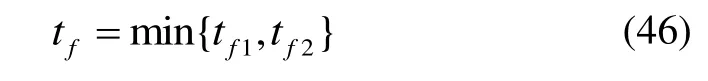
式中，tf1、tf2分别为拦截弹M1和M2的终端时刻。

3 仿真分析与验证

本节将对前面所设计的制导律进行仿真验证。为了方便叙述，以下将本文提出的基于SDRE方法的非线性协同微分对策制导律（Nonlinear Cooperative Differential Games Guidance Law Based on SDRE）简称为SDRE-NCDG制导律。这里假设拦截弹和目标自动驾驶仪均具有理想动态特性，不计重力影响，且弹目各自速度均为常值，仿真参数如表1所示。

表1 仿真参数Tab.1 Simulation parameters

3.1 制导律性能验证

为了验证所提制导律性能，下面根据目标机动与否将弹目运动情况分为如表2所示的四种情况，然后对制导律性能进行分析。

表2 弹目初始位置和目标机动情况Tab.2 Initial positions and target maneuvers

3.1.1 目标不机动

在表2中的情况Ⅰ、情况Ⅱ下，两枚拦截弹从不同距离对目标进行拦截的仿真结果分别如图2、图3所示。

图2 目标不机动时的弹目轨迹Fig.2 Trajectories of interceptors and target in case I and II

图3 目标不机动时的拦截弹加速度指令Fig.3 Acceleration profiles of interceptors in case I and II

由图2可以看出，当目标不机动时，采用SDRENCDG方法，拦截弹在两种初始弹目距离下均能对目标进行拦截（脱靶量均小于0.5 m）。在两种弹目距离下，拦截弹完成拦截所需侧向加速度指令如图3所示，从图中可以看出，当初始弹目距离较近时，拦截弹需要更大的侧向加速度来克服航向误差带来的影响。

3.1.2 目标机动

当目标以v=50 m/s2进行机动时，拦截弹从不同距离对目标进行拦截的结果如图4、图5所示。

图4 目标机动时的弹目轨迹Fig.4 Trajectories of interceptors and target in case III and IV

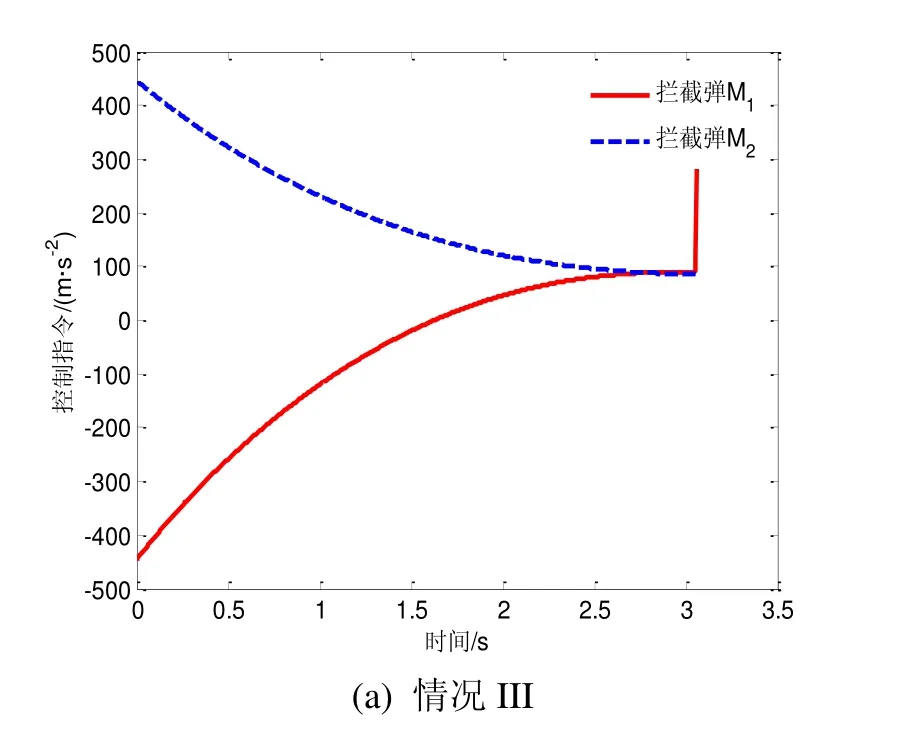
图5 目标机动时的拦截弹加速度指令Fig.5 Acceleration profiles of interceptors in case III and IV

由图4可以看出，当目标以v=50 m/s2进行机动时，拦截弹在情况Ⅲ、情况Ⅳ下均能对目标实施拦截（脱靶由量均小于0.7 m）。在情况Ⅲ、情况Ⅳ下，拦截弹完成拦截所需加速度如图5所示。与情况Ⅰ、情况Ⅱ相比可以看出，在情况Ⅲ、情况Ⅳ下，由于目标机动，在拦截末期拦截弹所需加速度较大，但这一现象符合预期。

3.2 制导律性能比较

为了进一步验证本文制导律的性能，下面将本文的 SDRE-NCDG制导律与文献[4]所提出的线性二次型微分对策协同（CLQDG）制导律进行对比。

仿真对比的背景条件如下：

1）SDRE-NCDG制导方法相关参数的选取仍如表1所示；

2）CLQDG制导方法相关参数的选取为：α=105，αE=105，βE=1.5；

3）拦截弹和目标的初始航向角、速度仍如表1所示；

4）拦截弹和目标的初始位置以及目标机动如表2中的情况Ⅲ、情况Ⅳ所示。

两种制导方法的仿真结果如图6～7所示。图6为两种制导方法在情况Ⅲ、情况Ⅳ下的弹目运动轨迹，从图中可以看出，两种制导方法均能对目标实施拦截（实现拦截的拦截弹均为拦截弹M1），但相较而言，CLQDG方法下的拦截弹弹道则更为弯曲。

图7为两种制导方法下的加速度指令，可以看出，SDRE-NCDG方法中的拦截弹M1完成拦截所需最大加速度均小于采用CLQDG方法的情况。在情况Ⅲ、情况Ⅳ下，拦截弹利用两种方法完成协同拦截所消耗控制能量如表3所示。由表3可以看出，本文SDRENCDG方法可以有效降低拦截弹所消耗的控制能量（约降低了25%的能量消耗）。

图6 两种制导方法下的弹目运动轨迹Fig.6 Trajectories of interceptors and target in two methods

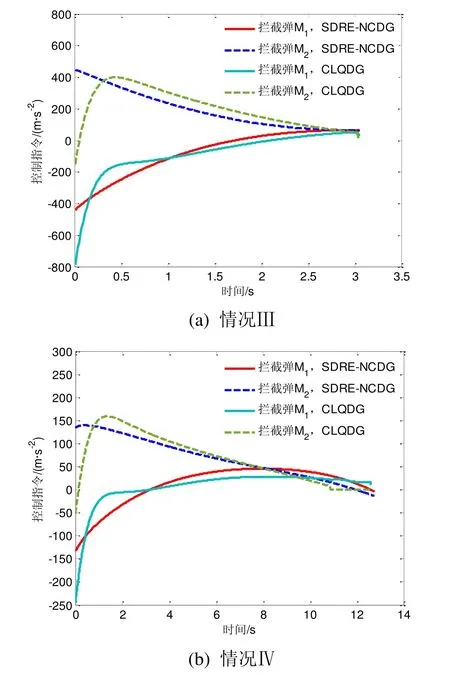
图7 两种制导方法下的拦截弹加速度指令Fig.7 Acceleration profiles of interceptors in the two methods

表3 两种制导方法消耗的控制能量Tab.3 Control energy of two guidance laws

注释 2 本文提出的制导律本质上不同于以同时到达或同时命中为目的的制导律。由于本文规定对策的结束时间为首先命中目标的拦截弹的终端时间，故在图4和图6中，虽可看到在拦截弹M1首先命中目标时拦截弹M2与目标之间仍然存在一段距离，但这段距离这并不代表拦截弹M2的最终脱靶量。此时，仍可进一步利用微分对策理论分析仅存在拦截弹M2与目标时的情况，只是对策问题已由二对一的协同对策转变成一对一的非协同对策，而一对一的微分对策问题可参阅文献[8-10]等。

4 结 论

本文针对非线性协同制导问题，基于SDRE方法提出了一种微分对策制导律。该方法将SDRE和微分对策理论结合应用于多弹协同制导，不需对剩余时间估计的精度进行考虑，避免了剩余时间估计误差对制导性能的影响。仿真结果表明本文方法能够对机动目标进行拦截，并可降低拦截弹的加速度要求以及控制能量的消耗，对于不满足小角度假设等线性化条件的协同制导问题具有一定的参考意义。