基于鲁棒无迹卡尔曼滤波的无线室内定位算法

高端阳，李 安，傅 军，周 鑫

（1. 海军工程大学 导航工程系，武汉 430033；2. 海军工程大学，武汉 430033；3. 92571部队，三亚 572000）

基于位置服务（Location-Based Services,LBS）的快速发展,一方面给人们的日常生活带来了极大便利，同时也促进了万物万联、人工智能、应急反恐等应用领域的快速发展。正是由于LBS可带来诸多好处，不管是人们的出行还是各行各业都对 LBS提出了更高的要求。根据美国环境保护局以及诺基亚的统计报告，人们有70%至90%的时间是在室内活动，70%的移动电话使用和80%的数据连接使用均发生于室内，因此人们迫切的需要将基于位置服务拓展到室内。由于室内环境复杂多变，无线电信号易受遮挡，产生非视距（Non light-of-sight,NLOS）传播和多路径效应，近年来，室内定位已成为广大学者研究的热点[1-2]。

超宽带（Ultra Wideband,UWB）是一种无载波通信技术，是当前短距离定位领域的研究热点之一[3-5]。在室内定位中，UWB可达厘米级定位精度，并具有较好的抗多路径性能以及一定的穿透能力[6-7]。为减小NLOS及多路径的影响，提高定位精度，文献[8]使用相关向量机技术来识别和减轻NLOS影响，提出了一种基于变分贝叶斯推理的分布式协作算法，相比于常用的基于到达时间（Time of Arrival,TOA）定位方法，该方法虽然可实现较高的定位精度，但是复杂度要高得多。文献[9]对 UWB基于往返时间（Round Trip Time,RTT）测量误差特性进行研究，分析RTT测量可能存在非高斯噪声的影响，并验证了采用粒子滤波算法处理的优越性，但是存在计算量大的问题。文献[10]提出了采用基于UWB测距信息和时延定位模型的扩展有限脉冲响应估计器实现目标位置估计，但是其精度取决于平均水平的设定。文献[11]提出了一种扩展卡尔曼滤波器（Extended Kalman Filter,EKF）超宽带室内定位方法，在复杂室内环境下定位精度可达亚米级。但是量测方程具有较强的非线性，EKF线性化误差较大，存在滤波发散的问题，同时EKF滤波算法雅克比矩阵求取复杂，计算量较大，不利于实际使用。

为了进一步提高UWB系统定位精度，本文提出了一种鲁棒无迹卡尔曼滤波定位算法。该方法根据 UWB系统定位误差特性以及结合室内环境实际情况，引入代价函数，修正观测方差，建立鲁棒机制，降低UKF算法对观测噪声特性分布的要求，增强 UWB系统的环境适应能力。设计相关实验，采用实测数据对所提出的算法进行验证，结果表明，提出的鲁棒UKF性能均优于UKF、EKF和最小二乘算法，UWB系统定位精度提升明显。

1 UWB定位实现

常用的无线定位算法主要有四种，分别是基于TOA、基于到达时间差（Difference of Time Arrival,TDOA）、基于到达角度（Angel of Arrival,AOA）和基于接收信号强度（Received Signal Strength Indication,RSSI）。UWB 是一种无载波通信技术，利用纳秒的非正弦波窄脉冲传输数据，可测量精准的信号传输时间，即可精确测量基站到标签的距离，因此UWB通常采用基于TOA的定位算法。

以平面定位为例，假设各个基站的坐标分别为BSi(xi,yi)，定位标签坐标设为Tag(x,y)，基站BSi到标签Tag的测量距离为ri，分别以基站BSi为圆心，测量距离ri为半径，作圆位置线，由于测距误差的存在，定位模型如图1所示。

图1 基于TOA的几何定位模型Fig.1 Geometric positioning model based on TOA

基站的个数通常不小于3个，由几何定位模型可得：

该方程为非线性方程组，常采用最小二乘法求解（Least Square,LS），即可求得标签Tag的位置。

2 标准UKF算法

在EKF算法的核心是对非线性的状态方程和观测方程进行泰勒展开，通过取其一阶项实现方程的线性化。若方程的非线性较强，这样就会造成较大的线性化误差，最终导致滤波器的性能下降甚至滤波发散。UKF算法舍弃了EKF算法的线性化过程，采用无迹变换（Unscented Transform,UT）巧妙的避免了线性化所带来的误差，同时减少了算法的复杂度，克服了EKF算法的估计精度低、稳定性差的缺陷，组合导航中被广泛应用[12]。

假设UWB基站个数为m，以UWB测距信息作为观测量Zk=[r1r2rm]T，状态量为目标的位置和速度Xk=[xyzvxvyvz]T。对于不同时刻k，系统噪声为高斯白噪声wk～N(0,Qk)，量测噪声为高斯白噪声vk～N(0,Rk)，构成UWB定位的非线性系统可以由式(2)表示：

UKF传播流程首先求解误差协方差矩阵的均方根Sk+-1，采用Cholesky分解来求解：

由式(4)计算sigma点：

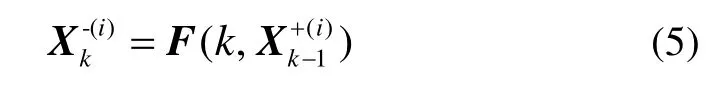
传播过后的状态估计及其误差协方差为

UKF的观测更新流程由式(8)产生新的sigma点：

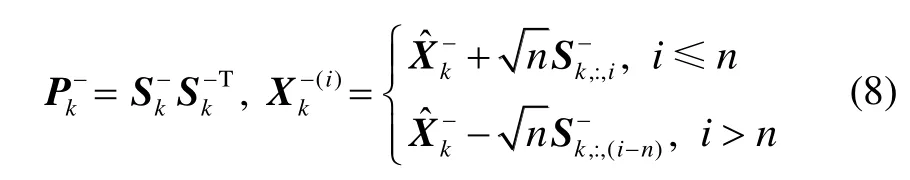
sigma点和平均观测新息可由式(9)解算：

则观测新息的协方差为：

最后，UKF卡尔曼增益、状态向量更新和误差协方差更新为

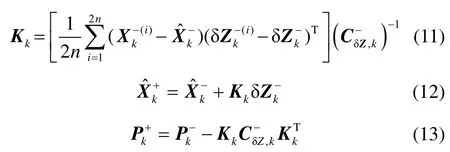
当系统噪声和量测噪声均为高斯白噪声时，通过上述标准 UKF定位算法可实现目标位置和速度的最优估计。

3 基于观测方差修正的鲁棒UKF

无论是 EKF还是 UKF，都是基于最小l2范数原则。基于最小l2范数的估计相比较于其他估计方法有着无法比拟的优势，但是基于最小l2范数的估计不具有鲁棒性，要求噪声的统计特性为高斯分布，且当假设条件和现实参数不一致时，状态估计精度下降。1964年Huber提出了广义极大似然估计，即M估计，同时并给出了解决一类在高斯分布附近存在对称干扰问题的鲁棒处理方法，即 Huber方法，该方法中，Huber用一种基于l1/l2的混合代价函数（Huber 代价函数）取代基于l2的代价函数以解决干扰高斯分布的问题。后续学者将Huber代价函数引入到卡尔曼滤波中以提高其鲁棒性。结合文献[13]，本文采用一种新的鲁棒UKF（RUKF）算法实现室内无线定位系统的位置估计。

基于式(2)非线性空间模型，构建非线性回归模型如下：

其中，δXk|k-1为状态真值与预测值之差。用εk表示式(14)右侧第二部分，则：

对式(14)两边分别右乘Sk-1，则：

其中，

根据广义极大似然理论，式(16)中的回归问题可最小化如下代价函数求解：

其中ek=yk-g(Xk)。令ψ(ek,i)=φ(ek,i) /ek,i，则：

其中，sgn(·)表示符号函数。令Ψk=diag[ψ(ek,i)]。对式(15)中的方差进行修正：

将修正的噪声方差替换标准 UKF中的噪声方差即为基于观测修正的鲁棒UKF。

4 实验验证

为了充分验证所提方法的合理性，采用一种常用的UWB定位系统进行实验，输出频率为50 Hz，最大定位距离可达35 m。实验场景如图2所示。

图2 实验场景Fig.2 Experimental scene

4.1 测距误差分布检验

目标静止情况下采集 1 min测距数据，首先对UWB系统目标测距误差分布特性进行检验，检验结果如图3～6所示。

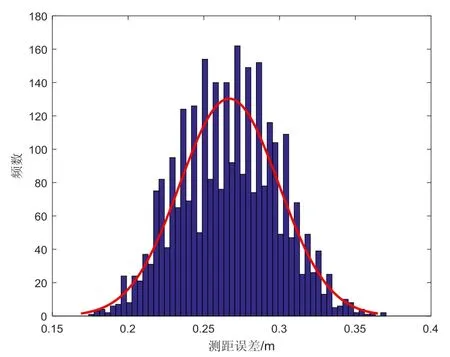
图3 基站1测距误差分布Fig.3 Ranging error distribution test of base station 1

图4 基站2测距误差分布Fig.4 Ranging error distribution test of base station 2

图5 基站3测距误差分布Fig.5 Ranging error distribution test of base station 3

图6 基站4测距误差分布Fig.6 Ranging error distribution test of base station 4

观察图3～6以及根据 MATLAB单样本分布的Kolmogorov-Smirnov检验结果，如果测试在15%显著水平上拒绝零假设，标签到4个基站的测距误差均为非正态分布。因此可知，标签的测距误差均为非高斯噪声。

4.2 静态实验

为验证本文提出的鲁棒UKF定位算法的合理性，在定位区域内任选9个参考点，依次将定位标签放置于参考点位置1 min，采集测距数据，并分别采用LS、EKF、UKF、和RUKF不同的定位算法进行解算，计算每个参考点的均方根误差（Root Mean Square Error,RMSE），计算结果分别如图7和表1所示。

图7 不同定位算法定位精度对比Fig.7 Comparison on static positioning accuracies of different location algorithms

表1 不同定位算法定位精度对比/mTab.1 Comparison on positioning accuracies of different location algorithms/m

从图7及表1可知，采用LS定位算法，各参考点RMSE最大值为0.60 m，最小值为0.26 m，均值为0.39 m；采用EKF定位算法，各参考点RMSE最大值为0.55 m，最小值为0.33 m，均值为0.41 m；采用UKF定位算法，各参考点RMSE最大值为0.50 m，最小值为0.29 m，均值为0.37 m；而采用本文提出的RUKF定位算法，各参考点RMSE最大值为0.45 m，最小值为0.24 m，均值为0.33 m。

4.3 动态实验

为进一步验证本文提出的鲁棒UKF定位算法的动态性能，采集运动轨迹为矩形的一组数据，分别采用 LS、EKF、UKF和RUKF算法进行处理，处理结果如图8～10所示。

观察图8～10可知，RUKF相比较于LS、EKF和UKF具有更强的鲁棒性，尤其是当观测值出现较大误差时，RUKF所表现出的优越性更加明显。因此，RUKF在动态定位性能上均优于其它3种算法。

图8 不同定位算法动态定位对比Fig.8 Dynamic positioning comparison of different location algorithms

图9 x向误差比较Fig.9 Comparison of x axis errors

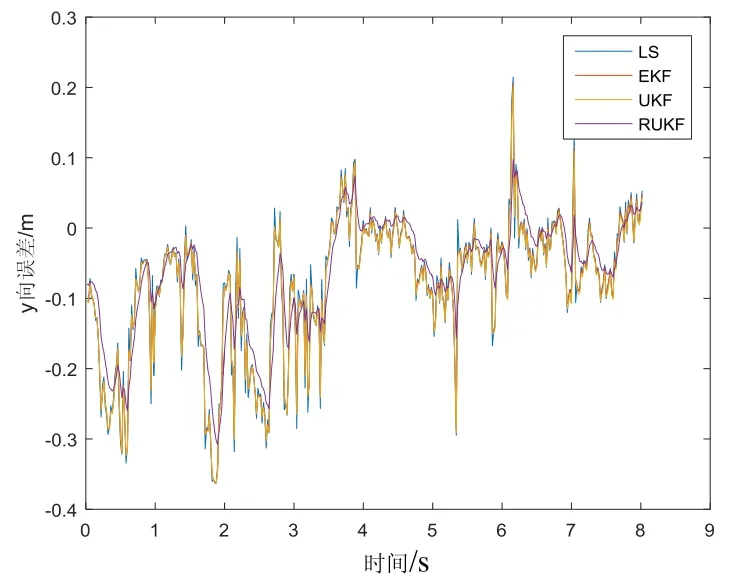
图10 y向误差比较Fig.10 Comparison of y axis errors

综合图7～10和表1，将EKF或UKF与LS对比可知，EKF和UKF相比较于LS定位算法并没有绝对的优越性，在某些参考点位置 LS定位算法的定位精度高于 EKF和UKF；将UKF与EKF对比可知，由于EKF线性化误差的存在，UKF定位算法精度优于EKF，但是观测方程的非线性程度不高，UKF定位精度提升并不是十分的明显；将RUKF与其他定位算法对比可知，由于引入了鲁棒机制，RUKF对观测噪声分布特性要求降低，能够对观测数据更好的进行滤波处理，定位精度有了明显的改善，尤其是当其他算法定位误差较大时，采用RUKF定位算法精度提升更加明显，因此RUKF定位算法相比较于其他算法具有更强的鲁棒性，环境适应能力更强。

5 结 论

本文对 UWB室内定位算法进行了研究，提出了一种鲁棒UKF定位算法，通过引入代价函数，修正观测方差，建立鲁棒机制，以提高UWB在实测环境下的定位精度。实验结果表明：EKF和UKF算法在某些参考点定位性能优于LS算法，但也存在某些参考点LS算法高于EKF和UKF算法定位精度的现象，因此采用标准的EKF或UKF定位算法不具有普适性；本文提出的鲁棒UKF算法，不再要求噪声的统计特性为高斯分布，改进了标准UKF在实测环境下存在的问题，能够实时自适应的对观测噪声进行修正，定位精度均优于LS、EKF和UKF定位算法，平均定位精度可达0.33 m，与LS定位算法相比，定位精度提高了15%。

本文提出的一种新的自适应UKF算法，考虑了UWB实测环境下误差特性，实现简单，计算量小，具有较强的实用性，是一种高精度的室内定位方法。