不同基准钟约束的卫星钟差精度分析

张 涛，谷守周，秘金钟，李 超1，，盛传贞

(1.山东科技大学 测绘科学与工程学院，山东 青岛 266510；2.中国测绘科学研究院，北京 100830；3.中国电子科技集团公司 航天信息应用技术重点实验室，石家庄 050081)

0 引言

全球卫星导航系统(global navigation satellite system，GNSS)高精度定位中，需要全球定位系统(global positioning system，GPS)的精密卫星钟差作为精密定位与精密定轨的重要基础数据，而我国的国际GNSS监测评估系统(international GNSS monitoring & assessment system，iGMAS)分析中心的综合精密卫星钟差产品在事后解算的过程中产生的异常值会影响钟差产品的精度和可靠性。为解决异常值问题，文献[1-3]提出采用抗差估计方法迭代计算等价权的方式代替传统的最小二乘法，以剔除观测数据中的少量粗差；并且文献[4]提出抗差估计理论以其抵御粗差的特性广泛应用于原子时算法中；文献[5]提出采用高崩溃污染率抗差估计迭代计算等价权得到综合钟差的方法，对钟差改正进行处理。

原子钟通常用于卫星、地面监测站的时间基准，而氢钟在长期运转的过程中，检测准确度高、信号质量好、短中期稳定性好。针对氢钟的优良特性，文献[6]提出氢钟可以作为优质的时频基准源并能够符合导航定位系统的性能要求。长期以来，由于守时系统的原子钟以铯钟为主，原子时算法也是以铯钟的频率特性为基础产生和发展的，原子钟算法的相对落后以及对原子钟特性的忽略，会导致产品的精度不高。文献[7]针对氢钟存在的频率漂移特性，基于抗差估计方法进行原子时计算，对氢钟原子时算法的函数模型、随机模型进行了改进，并得出结论：使用加权平均算法的氢钟不能明显发挥频率漂移的特性，而针对氢钟的改进算法所获得的平均时标的稳定度和准确度总体上有显著提高。

随着抗差估计理论的广泛应用以及高性能守时氢钟的出现，可通过研究抗差估计理论以匹配高性能的原子钟，提高综合产品的精度与可靠性。本文以不同类别测站钟为基准钟来约束事后快速钟差的解算，并基于抗差估计方法进行数据分析处理。

1 精密卫星钟差估计方法

精密事后卫星钟差的估计过程中，一般采用非差无电离层的函数模型进行计算。文献[8-10]提出高精度的卫星钟差在非差精密单点定位中尤为重要，相位观测值有利于高精度的卫星钟差参数估计。非差无电离层的函数模型，利用双频载波和伪距观测，能够消除伪距和相位的电离层一阶项，解算精度高，可靠性高，观测信息没有损失，实现模糊度的固定。观测值误差方程为：

(1)

(2)

对式(1)及式(2)变形可得卫星钟差的误差方程

(3)

式中l为常数项值。

在精密卫星钟差估计过程中，所讨论的GPS卫星钟差为相对钟差。GPS的观测值存在测站与卫星之间的相对延迟，不能同时对所有卫星和测站的绝对钟差进行确定，需要将某一卫星钟或者测站钟作为基准钟进行固定，得到其他卫星和测站的相对钟差。从相位观测方程式(1)可以得出，钟差参数与初始模糊度是相关的，可将式(1)和式(2)相减，对相位观测值的模糊度进行估计，确定模糊度的误差观测方程为

(4)

由于载波相位观测值相对于伪距观测值的精度较高，所以采用载波观测值误差方程进行卫星钟差估计。在精密卫星钟差估计过程中，假设有m个测站，对n颗卫星进行同步跟踪观测，并将第一个测站的接收机作为基准测站时，基准测站在某个估计历元时刻的载波观测误差方程为

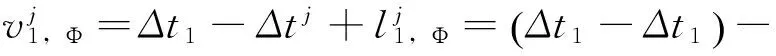
(5)

其他测站k的观测误差方程为

(6)

(7)

写成矩阵形式为

V=AX+LΦ。

(8)

式中：

(9)

(10)

其中

(11)

E为n阶单位矩阵；

(12)

(13)

2 抗差估计方法原理

设误差方程为

(14)

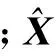
(15)

参数的解为

(16)

抗差估计的抗差特性关键在于函数ρ的定义和权因子函数自变量的选择。

1)定义函数ρ的目的是由函数ρ(v1,v2,…,vn)导出权因子函数。权因子的作用是限制超出正常范围的误差对平差的影响。当观测值Li在正常范围时，wi取值为1；观测值超出正常范围时，wi取值为小于1的非负数。通常权因子函数采用测量平差中应用较广的Huber函数和IGG3函数。

Huber函数为

(17)

IGG3函数为

(18)

式中：vi为观测值残差；kh、k0、k1为界值，界值一般取3倍的中误差。

2)权因子函数自变量的选择一般采用最小二乘平差结果作为权因子函数自变量的初始值。

3 实验与结果分析

本文采用iGMAS分析中心的快速钟差产品数据进行实验，实验中将氢钟、铯钟、铷钟等不同类别的原子钟作为测站基准钟进行快速钟差的解算，并将不同类型原子钟作为基准钟的钟差解算结果，利用抗差估计方法与iGMAS产品综合与服务中心发布的GPS快速钟差产品进行精度对比分析，得到相应的单位权均方根值(root mean square，RMS)作为精度指标，最后比较不同类型原子钟作为基准钟的快速钟差产品精度，以选取适应于抗差估计方法的原子钟。

实验时，采用2016年年积日第223天、第224天、第225天共3 d的GPS快速钟差产品数据，采样间隔为5 min。年积日第223天、第224天、第225天均进行相同基准钟变换实验，针对每一个基准钟均生成GPS快速钟差产品，并分别与iGMAS产品综合与服务中心发布的GPS快速钟差产品进行抗差估计方法的精度比较，则年积日第223天至第225天的比较结果如图2～图4所示。其中，实验所使用的基准钟类型有氢钟、铷钟、铯钟3种，测站钟HOB2、HRAO、DRAO为氢钟，测站钟BOGI、CHUR、JPLM为铷钟，测站钟HARB、MIZU为铯钟。实验中所用的这些测站钟的观测数据的完整率均为100 %。

由这3 d的各基准钟比较结果可以看出：

1)年积日第223天：①测站基准钟属于氢钟的HOB2、HRAO、DRAO站的各卫星RMS值普遍偏小，每颗GPS卫星的RMS精度值均小于100 ps；②测站基准钟属于铷钟的CHUR、JPLM站的每颗卫星的RMS值均小于200 ps左右，铷钟测站BOGI的每颗卫星的RMS值整体偏大，浮动在800 ps左右；③测站基准钟属于铯钟的HARB、MIZU站的大部分卫星的RMS值均小于500 ps，HARB站的试验结果中，G08、G24卫星均存在大值，超过1000 ps。

2)年积日第224天：①测站基准钟属于氢钟的HOB2、HRAO、DRAO站的各卫星RMS值普遍偏小，每颗GPS卫星的RMS精度值均小于100 ps；②测站基准钟属于铷钟的CHUR、JPLM站的每颗卫星的RMS值均小于200 ps左右，此时铷钟测站BOGI的每颗卫星的RMS值虽然整体偏大，浮动在200～500 ps左右；③测站基准钟属于铯钟的HARB、MIZU站的大部分卫星的RMS值均小于500 ps，HARB站的试验结果中，G08、G24卫星均存在大值，超过1000 ps。

3)年积日第225天：①测站基准钟属于氢钟的HOB2、HRAO、DRAO站的各卫星RMS值普遍偏小，每颗GPS卫星的RMS精度值均小于100 ps；②测站基准钟属于铷钟的CHUR、JPLM站的每颗卫星的RMS值均小于200 ps左右，此时铷钟测站BOGI的每颗卫星的RMS值浮动在200～500 ps左右，G09卫星存在大值；③测站基准钟属于铯钟的HARB、MIZU站的大部分卫星的RMS值均小于200 ps，HARB站的试验结果中，G08、G24卫星均存在大值，超过1 000 ps。

4)综合3 d的各基准钟的比较情况：①氢钟试验结果中，各颗卫星的RMS值均小于100 ps，整体精度高于铷钟和铯钟；②针对抗差估计的数据结果处理方法，铷钟和铯钟在各卫星RMS值不存在大值的情况下，从折线图的趋势得出，可能存在整体的系统误差，而氢钟的特性能够消除这种系统误差；③3 d实验结果中，氢钟的运转性能最为稳定，在100 ps以下浮动，铷钟的CHUR、JPLM站和铯钟的MIZU站较为稳定，在200 ps左右浮动；④铷钟的BOGI和铯钟的HARB站存在大值情况，大值情况在抗差估计中未能成功剔除。

对各基准钟每天的GPS所有卫星的RMS值分别求取平均值和中位数如表1所示。

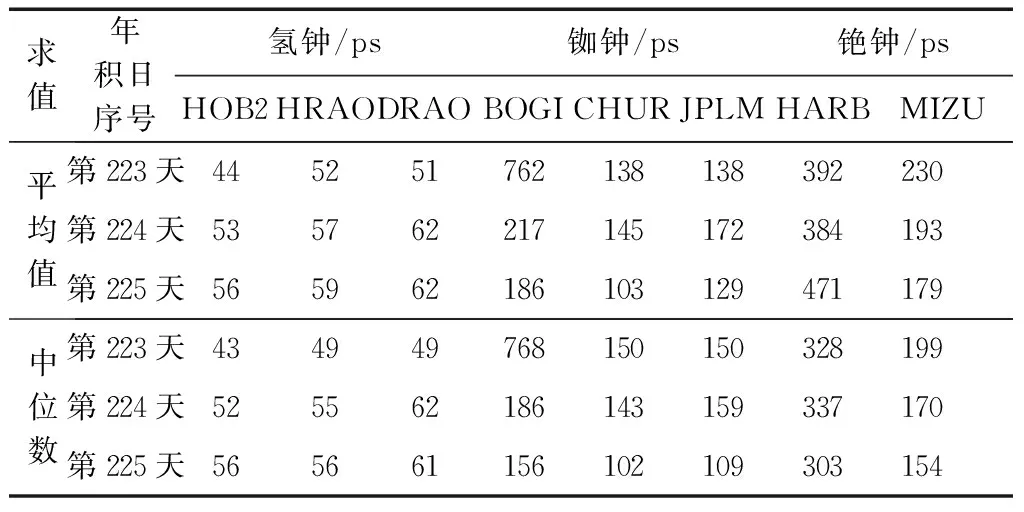
表1 各基准钟比较结果RMS值

从表1的各基准钟的比较结果可以看出：1)从基准钟类型来看，在观测数据完整的前提下，氢钟的实验结果明显好于铷钟和铯钟，3 d的实验结果均较为稳定，各卫星的RMS平均值在60 ps左右浮动，没有受到极端大值的影响，则氢钟的短周期运转性能稳定；2)从氢钟的HOB2、HRAO、DRAO各站的实验结果来看，氢钟之中也有实验结果的差异性，HOB2测站的实验结果在短周期内优于HRAO和DRAO的实验结果，因此HOB2测站可选为基准测站，为事后解算精度提高提供借鉴；3)基于抗差估计方法处理的实验结果中，相较于铷钟和铯钟，氢钟的实验结果最佳，因其特性可能有助于消除某种系统误差，所以精度比较结果更好。

4 结束语

本文对于GPS卫星钟差事后产品，采用抗差估计方法迭代计算等价权的特性，在产品解算过程中选取不同类型的原子钟作为基准钟进行约束，选取到适用于抗差估计方法的最佳类型的基准钟，使抗差估计方法和原子钟类型能够最优地发挥各自的特性，在一定程度上提高事后钟差产品的精度。通过实验证明，在事后快速钟差解算的过程中，在观测数据完整的情况下，基于抗差估计的数据处理方法之中，相较于铷钟和铯钟，氢钟更能发挥其特性，且在短周期内具有较高的精度和稳定性，而且实验发现HOB2测站的基准钟在氢钟中的性能更佳。

然而，基于抗差估计方法的不同类型基准钟约束的卫星钟差精度分析仅分析到氢钟更适用于抗差估计方法；而氢钟的何种特性适用于抗差估计方法并能够消除系统误差，将是研究氢钟作为基准钟解算钟差产品的重要方向。

[1] 杨元喜.抗差估计理论及其应用[M].北京：八一出版社，1993：92-122.

[2] 杨元喜，吴富梅.临界值可变的抗差估计等价权函数[J].测绘科学技术学报，2006，23(5)：317-320.

[3] 何海波，杨元喜.序贯平差抗差估计[J].测绘工程，1998，7(1)：36-40.

[4] 郭海荣，杨元喜.导航卫星原子钟时域频率稳定性影响因素分析[J].武汉大学学报(信息科学版)，2009，34(2)：218-221.

[5] 陈康慷.IGS分析中心轨道/钟差产品综合及网解模式动态精密单点定位研究[D].西安：长安大学，2014.

[6] 翟造成.我国氢钟研制现状与用于卫星导航的可行性[J].宇航计测技术，2003，23(5)：1-9.

[7] 郭海荣.导航卫星原子钟时频特性分析理论与方法研究[D].郑州：信息工程大学，2006.

[8] 叶世榕.CPS非差相位精密单点定位理论与实现[D].武汉：武汉大学，2002.

[9] 韩保民，欧吉坤.基于GPS非差观测值进行精密单点定位研究[J].武汉大学学报(信息科学版)，2003，28(4)：409-412.

[10] 楼益栋，施闯，周小青，等.GPS精密卫星钟差估计与分析[J].武汉大学学报(信息科学版)，2009，34(1)：88-91.