D形工件边界的识别定位方法研究
2018-03-05钱昭君李东平张秀英
钱昭君, 李东平,张秀英, 赵 鑫, 余 丹
(长春师范大学数学学院,吉林长春 130032)
机械工件是机械产品中的基本单元,目前大多数零件是通过机械加工的方法达到其最后要求的。工件在接受机械加工过程中,首先要使其在机床上获得一个正确位置,这个过程就是定位。工件的加工就是从定位后的原件表面切割下一部分金属。如果工件不能正确定位,切割就会偏离正确位置,导致工件无法按原计划加工。在进行工件加工过程中,合理地选择定位基准对于工件加工的尺寸精度和相互位置精度具有重要作用,直接地影响着工件加工的质量和效率[1]。
本文拟针对伺服电机驱动D型工件加工过程中遇到的实际问题设计有效的定位算法。在使用伺服电机驱动加工D型工件时(图1),需要对D型工件的边界进行准确定位。对于这个问题,目前主要是通过人工操作来完成工件的定位和刀具的切削。如何建立自动识别算法,通过自动检测实现工件的定位和刀具的加工方向来完成加工具有重要的意义,也是未来数控技术的发展趋势[2]。

图1 伺服电机驱动D型工件加工示意图和截面图
[指导教师]李东平(1983- ),男,讲师,博士研究生,从事计算数学研究。
自动确定工件定位模式在伺服电机驱动D型工件自动化加工过程中的有重要作用,而定位模式的确定关键就是根据已采集的位移数据对加工工件进行定位特征识别。本文试图通过分析由位移传感器所采集到的位移数据,建立稳定可靠的自动识别算法确定圆截面和缺失面的两个边界,并计算工件在测量位置的真实偏心量,即利用算法补充缺失位置的原始位移数据,从而还原出被加工面的形貌特征。本文所涉及的数值计算和图表均借助于MATLAB软件完成。
1 D型工件边界的定位识别算法设计
对于D形工件,若用y表示在第x个结点处的位移,则位移传感器所采集的圆形面所对应的位移数据其轨迹通常呈现为正弦或余弦的变化规律,即满足:
(1)
其中,n表示工件旋转一周时位移传感器所采集点的总个数,A,B,C为待定常数。对于缺口部分,其位移图像通常呈开口方向向下的抛物线状,因此可设其一般形式为
y=ax2+bx+c.
(2)
整个周期内的位移曲线由曲线(1)和(2)交错组成,通常有三种表现形式,如图2所示。两类曲线的交点即为工件的界点,也称为定位结点。

图2 单位周期内D型工件的三种位移图像
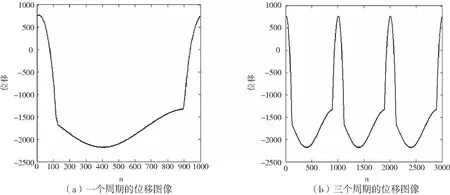
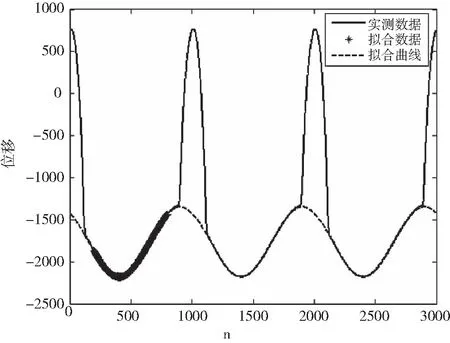
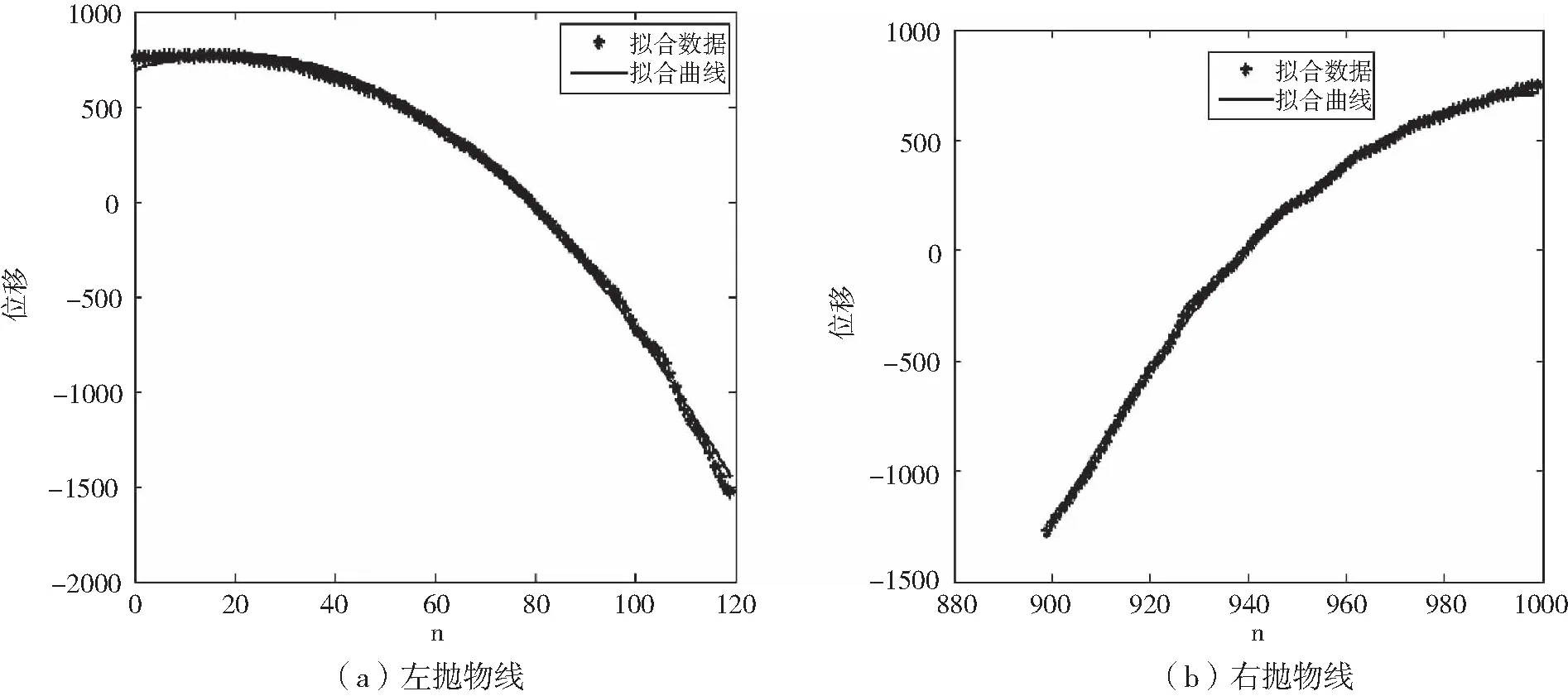
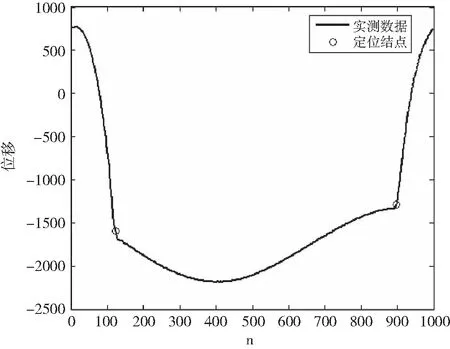
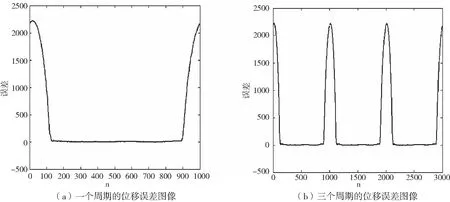
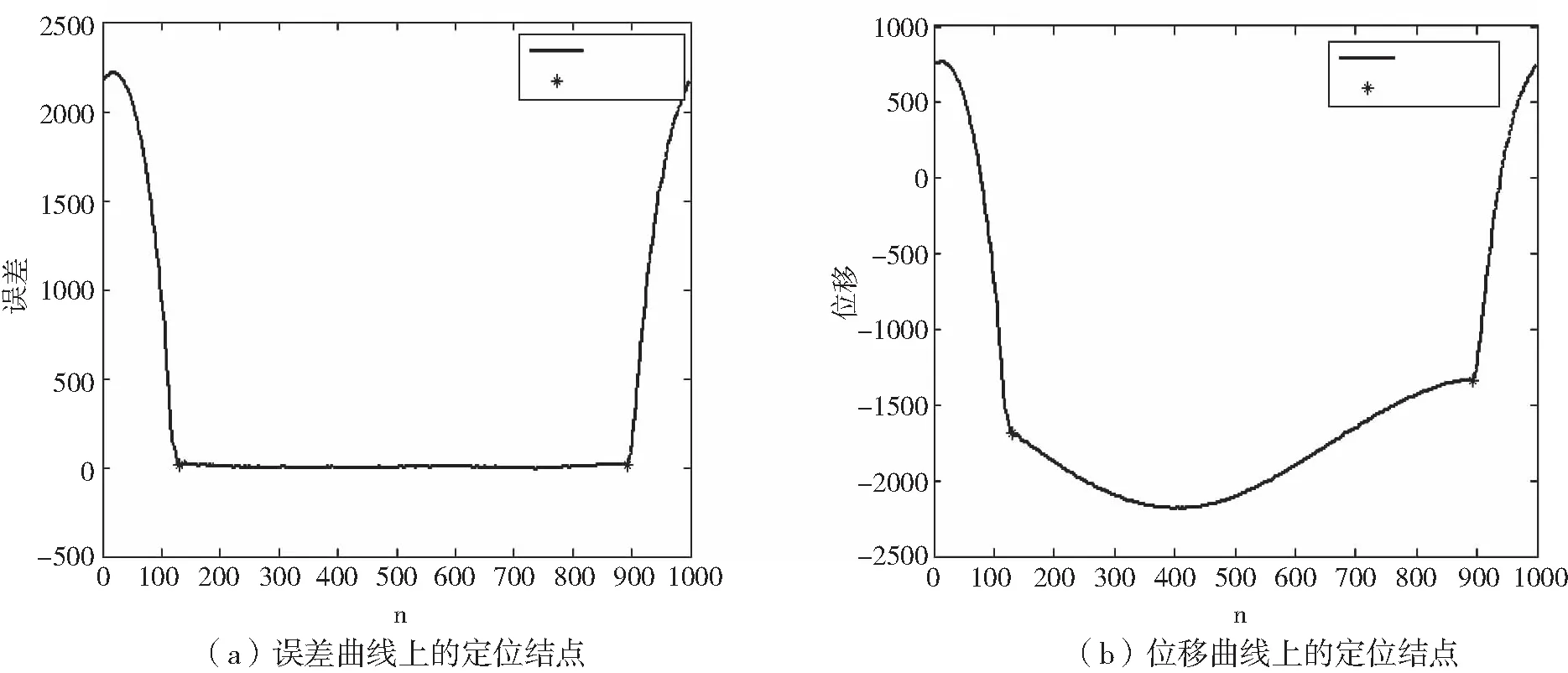
方程(1)和(2)的表达式可通过最小二乘法[2]进行曲线拟合得到。设y=ψ(x)=f(a0,a1,…,an,x)是待拟合函数,ai(i=0,1,…,n)是待定参数,(xi,yi),i=1,2,…,m,(n (3) (4) (5) 直接求解(5)可得到a,b,c的值。一旦获得函数(1)(2)的具体表达式,则界点可通过求解由方程(1)和(2)构成的非线性方程组获得。而缺失面的位移数据可由函数(1)直接补充。下面通过实际采集的位移数据来验证方法的有效性。 图3(a)是某D型工件加工过程中所采集的单位周期内(n=1000)的位移函数图像,图3(b)是三个周期内的位移数据图像,其位移变化规律与图2中的左图一致。 图3 某D型工件的实测位移图像 根据最小二乘算法,取初始值[A0,B0,C0]=[1000,0,-1300],利用[200,800]区间段内共计601组数据点对函数(1)进行最小二乘曲线拟合,得到 拟合产生的相对位移误差为 其中,‖·‖表示欧氏范数,yc表示用于拟合的实测位移,yf表示拟合曲线产生的位移。相对误差较小,说明拟合效果良好。图4给出了三个周期内拟合数据、实测数据和拟合曲线的函数图像。圆形部分的拟合位移和实测位移几乎重合,拟合效果较好,表明三角函数能正确反映圆形部分真实位移的变化规律。 图4 三个周期内拟合位移、实测位移和拟合曲线的函数图像 进一步,利用区间[0,199]内的数据点对左边抛物曲线进行拟合,其中拟合数据点的范围可通过定位最高位移点由程序自动确定,拟合结果为 相对误差为0.0465。类似地,利用区间[900,1000]内的数据点进行右抛物线拟合,拟合所得参数为 相对误差为0.0301。左右抛物线的拟合图像见图5。图像显示拟合曲线和拟合数据基本重合,说明抛物型曲线基本能反映非圆形面的位移变化规律。但从相对误差来看,其拟合精度略低于三角函数的拟合精度。 图5 左右抛物线的拟合图像 进一步,直接计算可得到抛物线与余弦曲线左、右交点的横坐标分别为 x1=1.241680100118395×102≈124,x2=8.975259164370609×102≈898. 这就得到了位移曲线的两个定位结点坐标,具体位置如图6所示。 图6 实测数据的定位结点图像 由图6可以看出,所计算的两个定位结点基本能准确反映它们的真实位置,些许的误差主要由抛物线的曲线拟合及方程组的求根导致,这一点可由接下来的数值结果证实。 为了减少因抛物曲线拟合及方程组数值求根导致的误差对定位结点的影响,一种简单但有效的方法是通过试探法[3]确定拐点的位置。试探法的基本特点就是在余弦函数拟合后不再进行抛物拟合而直接根据误差的变化规律确定界点位置。事实上,实测数据与拟合得到的余弦曲线的位移误差图像如图7所示。图像具有明显的结构特点,其中圆形部分所对应的误差图像基本跟横坐标轴重合(或围绕横轴小幅度波动),而其余部分则呈陡峭的上升或下降趋势。通过这些变化特征可用试探法直接确定两个定位结点的位置,计算结果显示它们的位置坐标分别为129和892,具体位置如图8所示。其定位效果比图5所示的结果更加精确,完全能反映真实界点的具体位置。 图7 余弦曲线的位移误差图像 图8 试探法确定的定位结点图像 本文通过研究D型工件表面位移的变化特征,基于最小二乘法建立了识别D型工件边界点的定位算法。该算法能解析地确定定位结点,可补充缺失面的位移数据。实验结果证实了算法的有效性和准确性,表明算法具有较好的应用前景和推广价值。下一步的工作可集中在相关程序的进一步改进和完善上,将其开发成可方便应用的程序包。 [1]唐宇,吴清潇,朱枫.平面工件的识别与定位方法研究[J].机械设计与制造,2015(10):172-175. [2]冯秀,顾伯勤.表面形貌的研究现状及发展趋势[J].润滑与密封,2006(2):168-170. [3]朱建新,李有法.数值计算方法[M].3版.北京:高等教育出版社,2017. [4]袁亚湘,孙文瑜.最优化理论与方法[M].2版.北京:科学出版社,2016.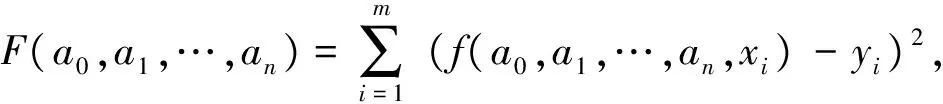
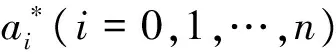
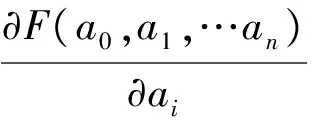
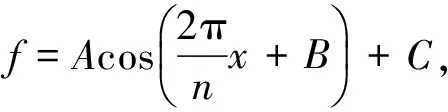
2 数值仿真



3 结论
