多项式系数Pf,γ,ξ相等的条件

齐 琳，许静波

(吉林师范大学数学学院，吉林长春 130103)

多项式系数Pf,γ,ξ在什么条件下相等，这是很值得关注和研究的问题.S Koike[1]已经对此进行研究，并给出多项式系数Pf,γ,ξ相等的命题.J P Henry[2]对实解析函数的bi-Lipschitz不变量进行研究.S Koike[3-4]对blow-analytic及其不变量进行了研究.N Kuiper[5]，T-C Kuo[6]对C1-等价与解析函数芽进行了讨论.本文对同胚条件做一个改变，并证明改变之后的命题仍然成立.

1 预备知识

定义2 设映射芽h:(E,0)→(F,0)，若存在L>0及E中包含0的开子集U，使得对任意u,v∈U均有‖h(u)-h(v)‖≤L‖u-v‖，则称h为Lipschitz映射芽.

定义3 设映射h:(E,0)→(F,0)，若h-1:(F,0)→(E,0)存在，且存在L1,L2>0及E中包含0的开子集U，使得对任意u,v∈U均有L1‖u-v‖≤‖h(u)-h(v)‖≤L2‖u-v‖，则称h为bi-Lipschitz映射芽.

定义4ordγf是非零系数的最小指数，系数Pf,γ,ξ(z)是关于z的一个多项式函数，那么对于∀ξ≥1，有f(λ(y)+zyξ,y)=Pf,γ,ξ(z)yordγf(ξ)+…，f为关于γ的序函数，即ordγf:[1,+)→R.

证明 由bi-Lipschitz性质，在0∈R2的(x,y)∈Hξ(γ;M)，

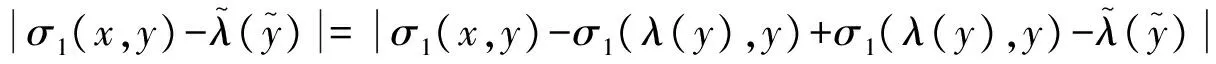
最后，对于∀ε>0，有0∈R2的一个邻域Uε，使得对于(x,y)∈Hξ(γ;M)∩Uε，

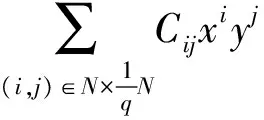
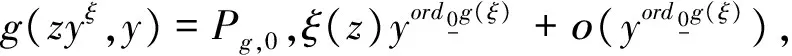
g((z+α(y))yξ,y+β(y)) =((z+α(y))(y+β(y)-β(y))ξ,y+β(y))

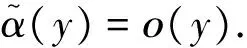
引理3 设f,g:(Rn,0)→(R,0)是形式f(x)=fm(x)+fm+1(x)+…,fm≠0，g(x)=gk(x)+gk+1(x)+…,gk≠0的解析函数芽，假设f和g是C1-等价的，那么k=m，fm，gm是线性等价的.尤其，如果齐次多项式函数是C1-等价的，那么它们是线性等价的.

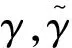
2 主要结果

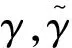
证明 因为由C1-等价⟹bi-Lipschitz-等价，所以由C1-同胚⟹bi-Lipschitz同胚，即σ:(R2,0)→(R2,0)既是一个C1-同胚，又是一个bi-Lipschitz同胚.

如果ξ=1，那么ordγf(ξ)=degPf,γ,ξ=mult0f，这个结果遵从bi-Lipschitz不变量的阶.

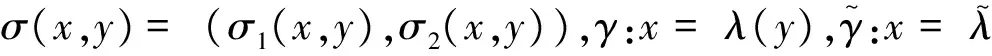
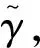
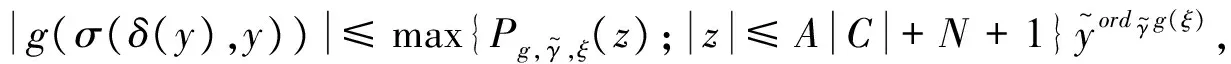
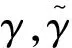
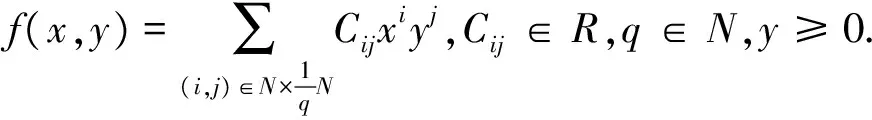
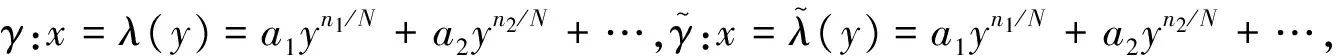
如果σ保持y-轴，则有形式σ(x,y)=(xφ(x,y),y+ψ(x,y))，其中φ(x,y)，ψ(x,y)是连续的，并且φ(0,0)=1，ψ(0,0)=0.

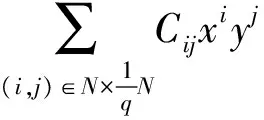
由引理2，α(y)=φ(cyξ,y)-1，β(y)=ψ(cyξ,y)，其中，c∈R是一个常数.那么，

f(cyξ,y)=g∘σ(cyξ,y)，σ(cyξ,y)=(cyξφ(cyξ,y),y+ψ(cyξ,y))，

f(cyξ,y) =g(cyξφ(cyξ,y),y+ψ(cyξ,y))

=g(cyξ(α(y)+1),y+β(y))

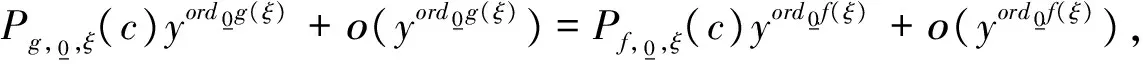
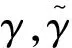
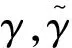
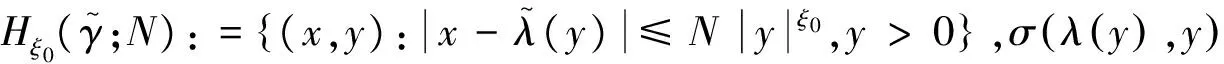
3 结论

本文主要对多项式系数在什么情况下是相等的条件进行了探究，证明了当其中的一个条件即同胚条件改变后，多项式系数相等的结论仍成立.对于如果其它的条件改变时，结论是否成立，会在以后的探究中逐步进行考虑.

[1]S Koike,A Parusiński.Equivalence relations for two variable real analytic function germs[J].J Math.Soc.,2013,65(1):237-276.

[2]J P Henry, A Parusi’nski.Invariants of bi-Lipschitz equivalence of real analytic functions[J].Banach Center Publications,2004,65(5):67-75.

[3]S Koike,A Parusiński.Motivic-type invariants of blow-analytic equivalence[J].Ann Inst Fourier,2003,53(8): 2061-2104.

[4]S Koike,A Parusiński.Blow-analytic equivalence of two variable real analytic function germs[J].J Math.Soc.,2010,19(3):439-472.

[5]N Kuiper.C1-equivalence of functions near isolated critical points[J].R D Anderson ed.,Annales of Math. Studies 1972,69(24):199-218.

[6]T-C Kuo,Y C Lu.On analytic function germs of complex variables[J].Topology,1997,16(9):299-310.

[7]S Koike.On strong C0-equivalence of real analytic functions[J].J Math.Soc.,1993,45(3):313-320.