基于电磁场的热力学性质研究

张 朋

(阜阳师范学院，安徽阜阳 236037)

信息社会离不开电磁技术的支持，该项技术已经被广泛应用到物质世界中，尤其是在21世纪，电磁技术已经实现与多种技术的交叉渗透，对推动社会发展有积极意义。电磁技术在作用过程中伴随能量的传递过程，其能量性质主要为热能，电磁波在作用过程中会产生能量损耗，在研究中可将其归结为热力学范畴，了解电磁场热力学性质对电磁波的应用有重要推动作用。

1 经典力学热力学平衡

对某一物质系统而言，在系统内部进行不同形式运动必然会造成相互作用，电磁场在物质系统中的作用也会产生能量传递转移的过程，该种能量传递过程主要通过热能实现，在物质内部则表现为内能。在经典力学中对电磁场的研究主要针对热力学平衡，建立平衡状态系统，该系统内部所有空间的强度量均为时间函数，与其所处空间无函数关系。通过热力学第一定义以及热力学第二定义，便可将系统中存在的基本微分关系推导出来。物理学第一定义描述系统内部热力学能量等于该系统从外界吸收的能量以及外界对系统所做的功，将系统从外界吸收的能量表示为Q，将外界对系统所做的功表示为(-W)，则在基础上可将热力学第一定义表示为：

Uf-Ui=Q-W.

(1)

dU=δQ-δW.

(2)

其中，Uf-Ui表示系统内部能量变化情况，结合热力学第二定义函数式(3)可将系统在运行过程中的可逆过程表示为式(4)形式。若仅存在外界对该系统所做的功，则可将其表示为式(5)形式。

dS=δQ/T.

(3)

δQ=TdS.

(4)

δW=pdV.

(5)

在以上分析基础上便可将热力学第一定律优化成为式(6)形式，即

dU=TdS-pdV.

(6)

其中，U表示热力学能，T表示温度，p表示压强，S表示熵，V表示体积。以上便是热力学的基本微分方程。为促进研究有效应用于实际，可定义系统焓为H，表达式为(7)，分贝设定自由能以及吉布斯函数可表示为式(8)和式(9)，结合热力学基本方程便可得出式(10)微分函数表达式。

H=U+pV.

(7)

F=U-TS.

(8)

G=U-TS+pV.

(9)

dH=TdS+Vdp,

(10.1)

dF=-SdT-pdV,

(10.2)

dG=-SdT+Vdp.

(10.3)

通过式(10.1)～(10.3)便可得出辅助函数物理实际意义，在电磁场和系统中减少的焓等于系统等压条件下释放的热量；系统中自由能的降低等于系统温度不变情况下系统对外界所做功；在系统等温条件下，吉布斯函数的减少量等于体积功以及系统对外界所做其他形式功之和。在进行系统热力学研究中需要重点分析其能量性质变化，主要包括热能、体积功、化学能等性质能量变化，可将系统热力学关系表达为：

dU=TdS-pdV+∑ujdNj.

(11)

其中，uj表示第j种组分化学势，Nj表示第j种组分摩尔数。为导出多组分系统辅助函数微分，可结合辅助函数定义以及其基方程进行求导，以吉布斯函数为例，可将其微分形式表示如下：

dG=-Sdt+Vdp+∑ujdNj.

(12)

得出组分系统辅助函数微分关系后不仅可通过微分关系求解出热力学函数，还可展开热力学行知研究。结合热力学第一定律可展开系统能量分析，进行系统作用分析，并对系统运行过程进行判断。

2 均匀电磁场作用下的平衡态热力学关系

首先进行简单电介质系统的平衡态热力学关系研究。在实际研究过程中热力学体系属于电磁场作用下一定质量电介质，则在此过程中可假设其体积变化很小，将体积变化量忽略不计，系统在进行能量传递过程中只通过吸热和放热形式进行能量的交换，便可称该系统为简单电介质系统，并通过函数表达式可将该系统中的热力学能U表达为：

dU=TdS+Edp′.

(13)

H=U-EP′.

(14)

F=U-TS.

(15)

G=U-TS-EP′.

(16)

dH=TdS-p′dE,

(17.1)

dF=SdT+EdP′,

(17.2)

dG=SdT+P′dE.

(17.3)

(18)

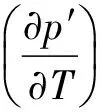
(19)

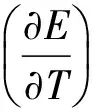
(20)

通过以上微分方程以及熵方程对系统中的热力学性质进行研究，对式(19)进行演变，得出：

(21)

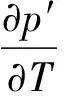
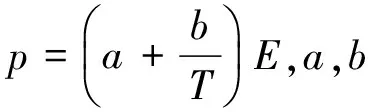
(22)

解得出偏导数

(23)

对于b>0的材料，在系统绝缘的情况下，随着电场强度不断增加，电介质温度会呈现上升趋势；对于b<0的材料，在系统绝缘的情况下，随着电场强度不断增加，电介质温度会呈现出下降趋势。设定系统为等温环境，则可将式(19)转变为：

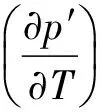
(24)

在温度不变情况下，系统中的电场变化会导致其熵出现变化，结合电介质状态方程可得出：

(25)

在系统稳定不发生变化的情况下，提升系统电场强度会减少系统中的熵。对电介质系统进行热力学研究不仅可通过电场取代其压强，还可通过极化强度代替体积，该性质可被直接推广到所有的电介质系统。在研究中应用功广义形式以及复杂系统热力学基本方程进行电介质热力学性质系统的研究。

当前大多数材料不仅具备电介质特性，还具备磁介质特性，即电磁同性，该类物质在相互作用过程中，电磁场会提升系统内能，并进一步提升系统热力学特性，对于一个封闭性系统而言，体系中的电磁场会对电场的热容造成影响，通过上述分析便可得出均匀电磁场的热力学性质。

3 电磁场作用下的非平衡态热力学

上述研究均是建立在均匀电磁场的基础上，而自然界中大多数电磁场是非均匀的，电磁波在传播及吸收过程中，其在空间分布式是一种非均匀状态，即电场强度与磁场强度在本质上既是时间的函数，又是空间的函数，因此需要研究非平衡过程的热力学性质，对系统中的各项参数进行研究分析，结合非平衡热力学理论展开分析。电磁场的传播过程属于一种动态变化过程，其在空间分布属于非均匀状态，即电磁强度属于一种多元函数，整个空间处于非平衡状态，需要通过非平衡热力学理论进行分析。

从整个空间上来看，电磁场处于一种与时间和空间均存在函数关系的系统中，该系统处于动态变化中，对其时间及空间进行微元化处理后便可得到微元化的局部系统，将所有体系划分为足够多微小体积元，这些体积元在微观上可视为足够大，并且对任意体积元而言，其内部包含足够小的分子，可满足研究需求。并且可设定其在微观上满足热力学关系，因此可运用经典热力学进行研究。以上整个假设过程便是局域平衡假设，设定以上假设过程需要满足量条件，条件一是要求试验体系中所有热力学量空间梯度很小，条件二是所有体积元的物理量衰落速度远远超过宏观物体，即衰落微观梯度远超出宏观梯度。通过局域平衡假设可将所得结果推广至非平衡态热力学。

在热力学平衡系统中需要构建平衡结构，这种结构一般是客观存在的实质性物体，不需要进行能量交换和物质交换便可客观存在，较为常见的平衡结构就是晶体结构，在热力学研究中还需要注重耗散结构，耗散结构是一种与平衡结构相对应的结构，该种结构需要通过能量交换和物质交换才能维持，一般通过能量梯度维持其基本形态。即平衡结构属于一种死结构，而耗散结构则属于一种活结构，在进行非平衡热力学研究过程中需要结合耗散结构进行分析，即能量的传递是一种动态过程，并非死过程。结合耗散结构理论对非平衡态热力学进行分析，通过拉格朗日定理由微分形式表示其平衡方程，即：

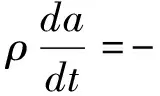
(26)

其中，ρ表示物理量密度，该平衡方程左边表示物理量密度随时间变化关系；Ja表示相对于体系的流量密度；σa表示物理量的源密度，即物理量在单位时间单位体积内产生量，则在以上分析基础上可结合经典非平衡态热力学获得系统的质量、动量、能量、动能、内能、熵等几个方面的平衡方程。在本系统中主要研究其内能、熵等方面。对于开放系统而言，在系统热力学性能较弱时其偏离平衡状态非常小，此时系统热力学力与热力学流之间存在唯象关系，可将其表达为：

Ji=∑LijXj.

(27)

其中，Lij表示唯象系数，Ji表示热力学流，Xj表示热力学力。在该公式中Lij表示系统中各种不可逆过程交叉耦合效应，可通过矩阵形式将唯象系数表示出来，并且矩阵为对称矩阵形式，即存在Lij=Lji关系。在对线性平衡性质研究过程中需要考虑熵与时间之间的关系，将总熵产生表示为：

(28)

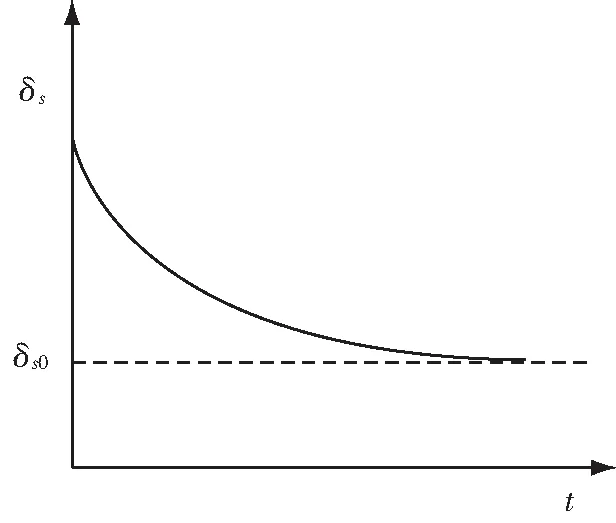
图1 熵产生随时间的变化趋势图

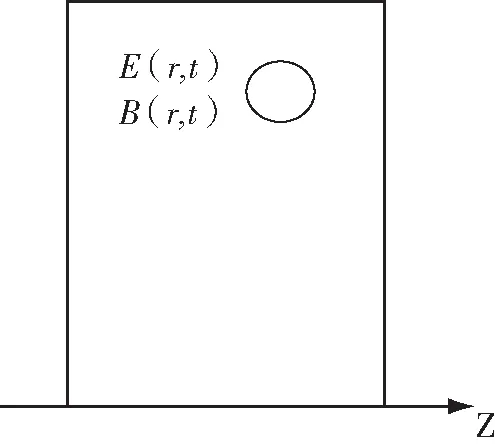
图2 小体积元模型结构

设定一个非均匀电磁场，该空间电磁场强度与空间及时间均存在函数关系，空间所涉及的过程均是非平衡过程，即系统中的所有强度量参数不仅与实践存在相对关系，与空间也存在相对关系。为满足以上假设，设计如图2所示的小体积元作为研究对象，结合前文小体积元假设可知，该系统在微观角度足够大，在宏观角度比较小。

在与时间有函数关系、与空间无函数关系的系统中，所考虑的外力均被设置为保守力，该种情况是可逆的，而对于电磁场强度与空间及时间均存在函数关系的情况则属于不可逆过程，因此针对该种情况需要重新研究。结合质量平衡方程和连续不变方程，设定体系中k组分质量平衡方程可表示为：

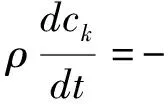
(29)

其中，γkjJj表示组元k在第j类化学反应中的产生率，Jj为反应j的化学反应率。ck表示组元中k组分质量分数，ck=ρk/ρ，Jk表示相对于中心部分的扩散流，Jk=ρk(vk-v)。vk表示k组分速度，v表示质心速度。系统连续方程可表示为：

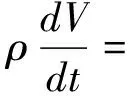
(30)

其中，V表示比体积。从整个体系运转情况来看，系统中的能量平衡方程发生变化，此时系统中的总能量不可简单看作动能、内能、势能的加总，结合系统运行状况来看，可将系统内能方程表示为：

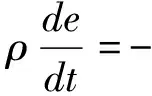
(31)

其中，Fk表示系统电磁场收到的力。系统动量平衡方程可表示为：

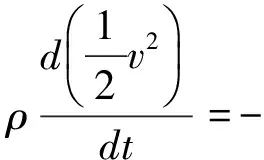
(32)

将能量平衡方程与动量平衡方程相减便可得出内能平衡方程，

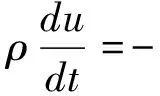
(33)

其中，Jk=ρk(vk-v)。本系统中的电磁场可以改变系统中各个参数量值的空间分布，符合系统保守力一般规律，结合平衡假设对电磁场中的熵平衡方程得出熵的表达式，

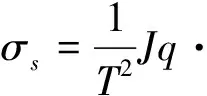
(34)

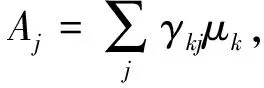
(35)

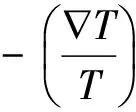
(36)

(37)

4 结语

在电磁场中，可结合平衡态势热力学理论分析电磁场作用下体系热力学机制，结合守恒定律得出密度产生率，并得出系统热力学流即热力学力线性方程，分析系统中电磁场热力学性质。本研究通过对均匀电磁场作用下的平衡态热力学关系以及电磁场作用下的非平衡态热力学进行研究，得出其热系统能量结构，得到热力学表达公式。

[1]李鹤龄,王娟娟,杨斌,等.由N-E-V分布及赝势法研究弱磁场中弱相互作用费米子气体的热力学性质[J].物理学报,2015(4):8-16.

[2]李劲,杨则金,朱正和.核磁子17O,33S和77Se的统计热力学计算——磁场下的热力学基本方程[J].四川大学学报:自然科学版,2016(4):829-834.

[3]田青松,门福殿,陈新龙.重力场和强磁场中费米气体的热力学性质[J].计算物理,2015(6):751-756.

[4]王磊.匀强磁场与简谐势阱中荷电自旋-1/2费米子的热力学性质[J].低温物理学报,2016(4):58-63.

[5]谭德宏,王凯俊,颜华,等.简谐外磁场环境下J-C模型的热力学纠缠[J].后勤工程学院学报,2015(4):70-73.