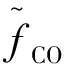模糊条件下机动车尾气含量模型

李瑞娟，张丽媛

(廊坊师范学院数信学院，河北廊坊 065000)

目前，机动车已经变成了人类生活中必不可少的工具，作为主要的交通工具发挥着极其重要的作用。机动车的出现为人们的生活和工作提供了极大便利，但是随着机动车数量的与日俱增，其弊端也逐渐显现出来，主要表现为道路拥挤、尾气污染、噪音污染等，其中最为严峻的是机动车的尾气污染.越来越为严重的机动车尾气污染成为空气污染的主要原因，机动车尾气污染危害城市的环境，可能会引发人类呼吸系统等方面的疾病.因此，机动车尾气污染防治工作凸显得尤为重要.面对着如此严峻的机动车尾气污染的情况，各国都在不遗余力地积极预防和治理着机动车尾气对空气造成的污染.国内外众多的学者开始关注机动车尾气问题的研究。蔡晓华、何杰、王轶等人研究了交通管制对隧道机动车尾气排放的影响[1]；徐涛就汽车尾气污染物排放浓度与过量空气系数对汽车尾气的影响进行了研究[2]；张本、商蕾、陈丹通过微观交通仿真研究城市交叉口机动车尾气的排放[3]；马因韬、刘启汉、雷国强等对机动车的多种排放模型进行了比较[4]；张恺、张玉钧、何莹等运用神经网络法对机动车尾气中的NO和NO2进行定量分析[5]，还有一些学者对此也进行了研究[6-7].这些研究往往针对确定性环境下的尾气污染问题，而在实际情况中，对于机动车数量、保有量等数据，人们只有模糊的认识，此时的研究理论就不太符合研究的要求，用模糊理论来描述机动车数量的不确定性更符合实际.本文针对城市空气污染中机动车尾气污染进行研究，运用模糊可能理论，在给定置信水平下计算空气污染物的最大含量，建立模型，并给出了算法，最后通过廊坊市机动车监测数据分别计算出实际污染物含量和在给定置信水平下的机动车最大污染物含量，通过比较验证算法的可行性.

1 预备知识

定义1[8]设Θ为非空集合，P(Θ)是Θ的幂集，映射Pos:P(Θ)→[0,1]，称为Θ上的可能性测度，如果Pos满足下列条件：(1)Pos{Θ}=1和Pos{φ}=0；(2)对于P(Θ)中的任意集族{Ai}，Pos{∪iAi}=supi{Ai}，则三元组(Θ,P(Θ),Pos)称为可能性空间.

定义2[8]ξ是从可能性空间(Θ,P(Θ),Pos)到n维实向量空间的函数，称ξ是一个模糊向量；当n=1，称ξ为一个模糊变量；并称ξα={θ|θ∈Θ,Pos{θ}≥α}为ξ的α水平集.

定义3[8]可能性空间(Θ,P(Θ),Pos)上的模糊变量ξ的隶属函数为μξ(x)=Pos{θ∈Θ|ξ(θ)=x}.

2 污染物含量模型

2.1 模型假设与符号说明

机动车是机械车类的总称，行驶的动力主要依靠燃烧燃油来得以实现，其排放的尾气主要成分是大致相同的，主要有一氧化碳(CO)、氮氧化合物(NOx)、碳氢化合物(CxHy)，此外还有硫氧化合物(SOx)、二氧化碳(CO2)、含铅化合物以及颗粒物等.

本文就某一城市在一个时间段内的机动车尾气污染物含量问题进行研究.在研究中只考虑城市机动车尾气排放造成的污染，暂不考虑其它因素对城市空气污染的影响.并且，只考虑机动车尾气中的主要污染物CO、CxHy、NOx(NO2和NO)的含量.

在建立模型之前，对模型中的相关符号作以下说明：

i=1代表私家车；i=2代表出租车；i=3代表公交车.

j代表所选取的路段，1≤j≤n.

Aij为某一时间段内第j段路上第i型机动车的数量.

qi为第i型机动车的CO排放因子.

si为第i型机动车的CxHy排放因子.

ti为第i型机动车的NOx排放因子.

lij为某一时间段内第j段路上第i型机动车的行驶路程.

模糊变量ξij(γ)为某一时间段内第j段路上第i型机动车的数量.

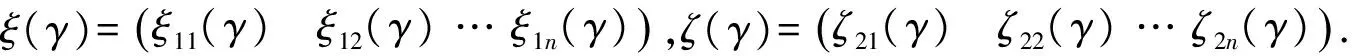
2.2 模型的建立与求解

2.2.1 模型的建立

对于一个城市，首先考虑在确定性环境下，私家车、公交车和出租车尾气污染中污染含量问题.污染物含量应该为各种车型污染物的排放量的总和.

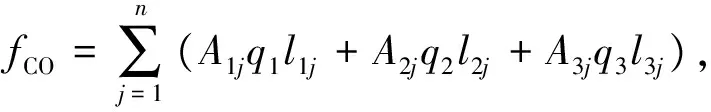
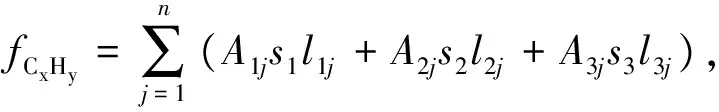
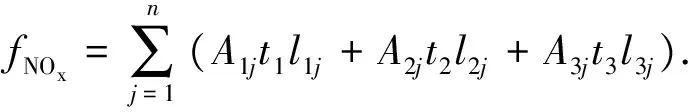
通过监测某城市某个时间段内机动车流量，参照排放因子表，可计算出污染物排放的总量.事实上，路段上每天的出行车辆的数量是不固定的，由监测数据计算出来的污染物排放的总量也只能代表此监测时间段内的污染物含量，因此在确定环境下计算出的空气污染物含量也就是不准确的.在此我们考虑在模糊环境下，以CO为研究对象，CH和NOx的研究方法相同.城市公交车因是统一安排，每个时间段的出行数量不发生变化，私家车和出租车的出行数量分别为模糊变量ξ1j(γ)、ξ2j(γ)(j=1,2,…,n)，则空气污染物中CO含量为：

(1)

在模糊环境下，计算空气污染物含量不超过某个规定含量的最大值.建立在置信水平α(0<α<1)下，不超过规定污染含量最大值的最大污染物模型：

(2)

2.2.2 模型求解

第一步：令fmax=+，给定α(0<α<1)值；

第四步：比较f和fmax，如果f

第五步：重复上述第二步到第四步共n次；

第六步：返回最后的fmax值.

3 数值实验

为了更好地说明上述模型的科学性和可行性，现考虑廊坊市的机动车尾气污染问题，研究路段为西昌路、永兴路、爱民道和光明道的方形路段上，在早高峰时间段(7∶00-8∶00)和非高峰时间段(3∶00-4∶00)内的机动车尾气污染含量问题.其中，研究车型的尾气排放因子见表1，在路口设置采样点，记录过往车辆数见表2和表3.

表1 车辆尾气排放因子

表2 高峰时段过往车辆数

表3 非高峰时段过往车辆数

由于行驶中车辆数的不确定性，因此取置信水平为α=0.5，模糊变量ξ1j的隶属函数分别为μξ11=exp[-(x-852)2]，μξ12=exp[-(x-825)2]，μξ13=exp[-(x-960)2]，μξ14=exp[-(x-656)2]；模糊变量ζ2j的隶属函数分别为μζ21=exp[-(x-412)2]，μζ22=exp[-(x-432)2]，μζ23=exp[-(x-499)2]，μζ24=exp[-(x-412)2]，则机动车尾气排放污染物CO含量为：

利用所给的求解方法对上述模型进行求解，并重复n=5000次，可求得给定置信水平α=0.5的机动车尾气排放污染物含量.

表4 污染物含量

由污染物含量表(表4)可计算得污染物含量的相对误差，见表5.

表5 相对误差

通过表4可知，高峰期和非高峰期机动车尾气污染含量变化非常大，可见机动车尾气污染中机动车数量的变化对空气污染的影响比较大，同时也说明，在控制空气质量时采取限行措施是比较合理的.对实际车辆检测数据和模糊环境下的数据进行比较，相对误差最大为3.144%(表5).还可以看出，在高峰期通过此模型计算污染物含量数据更接近真实值，因此，此模型在交通流量比较大的城市中更实用.

[1]蔡晓华,何杰,王轶,等.交通管理与控制对城市隧道机动车尾气排放的影响[J].重庆交通大学学报,2012(6):1198-1202.

[2]徐涛.浅论α值对汽车尾气污染排放的影响[J].干旱环境监测,2002,16(3):145-147.

[3]张本,商蕾,陈丹.基于微观交通仿真的城市交叉口机动车尾气排放评估[J].交通与计算机，2008,26(4):95-98.

[4]马因韬,刘启汉,雷国强,等.机动车排放模型的应用及其适用性比较[J].北京大学学报:自然科学版,2008,44(2):308-316.

[5]张恺,张玉钧,何莹,等.基于快速不动点法及神经网络的机动车尾气NO和NO2定量分析研究[J].大气与环境光学学报,2016,11(6):435-441.

[6]平措.我国城市大气污染现状及综合防治对策[J].环境科学与管理,2006,31(1):18-21.

[7]Ping Cuo.Status and comprehensive control countermeasures of urban air pollution in China[J].Environmenal Science and Management,2006,31(1):18-21.

[8]Zadeh L A.Probability measure of fuzzy events[J].Journal of Mathematical Analysis and Applications,1968,23(2): 421-427.