某高程控制网的静态卡尔曼滤波计算

李 军 亮

(山东省地质矿产勘查开发局第五地质大队，山东 泰安 271000)

在工程场地上，随着工程的不断开展，需要不断地布设高程点来满足测量工作的需要。传统的方法是每次布设完毕后将全网中的所有点进行整体平差，这样随着水准网的不断扩大，观测数据越来越多，就使得计算时的方程矩阵的阶数越来越大，从而给计算造成了较大的繁琐。序贯平差作为一种新的平差方法，可以解决这类问题，尤其对于超大型的网，从而使得网不断扩展的同时而计算可以分步进行，但是不会出现整体平差时带来的观测数据超多、计算超麻烦的情况。作者根据实际工作中的一些经验，结合某一个工程实例，从整体平差和分组平差两个方面进行了问题的分析与解算，以期与同行的工程技术人员分享。

1 理论原理

(1)

(2)

(3)

li=BiX0+di-Li(i=1,2)

(4)

将式(2),式(3)进行整体平差，即为经典的间接平差。

(5)

得第一次参数的改正数及平差值为:

(6)

(7)

(8)

联合式(3)，可得：

(9)

由式(8)，式(9)两式联合，应用间接平差可得参数的第二次改正数为：

(10)

(11)

最后可得平差值为：

2 实例计算

2.1 工程实例

某工程场地由于施工需要，布设了若干水准点，如图1所示，A,B为已知点，HA=21.400 m，HB=23.810 m。第一期独立同精度观测了h1～h5，第二期独立同精度观测了h6,h7，观测高差及路线长度分别为：

h1=+1.058 m，h2=+0.912 m，h3=+0.446 m，h4=-3.668 m，

h5=+1.250 m，h6=+2.310 m，h7=-3.225 m；

S1=S2=S3=2 km，S4=S5=1 km，S6=S7=3 km。

试按照序贯平差求P1,P2,P3点的高程。

2.2 计算

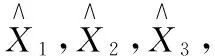
1)按照经典间接平差计算各待定点高程的平差值。

整体平差时的误差方程如下：

设C=1 km，则权逆阵Q=diag(2 2 2 1 1 3 3)；利用整体平差得各待定点高程的平差值为：

2)按照静态卡尔曼滤波计算各待定点高程的平差值。

第一期观测数据的误差方程如下：

第二期观测数据的误差方程如下：

设C=1 km，则权逆阵Q=diag(2 2 2 1 1 3 3)；利用分组平差得各待定点高程的平差值为：

3 结语

通过以上的计算和分析可以看出，运用静态卡尔曼滤波可以很好地解决数据的平差问题，其与经典的间接平差的结果是一致的。但是，需要说明几点：1)该题所举的例子中，仅仅是为了说明问题，用两种方法都不太麻烦；2)对于观测数据较多的情况，尤其是第二期、第一期的数据都很多的时候，这种方法的优越性格外明显。

[1] 张书毕.测量平差[M].徐州：中国矿业大学出版社，2008.

[2] 苗元欣.基于一元线性回归的变形监测数据处理与分析[J].矿山测量，2013(33)：161-162.

[3] 王 永，泥立丽，钟来星.利用Excel绘制误差椭圆的方法[J].矿山测量，2008(34)：21-23.

[4] 泥立丽，王 永.基于Excel的绘制误差曲线的方法[J].矿山测量，2010(16)：77-78.